iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://ncatlab.org/nlab/show/meson
meson in nLab

nLab meson

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Contents

Context

Fields and quanta

fields and particles in particle physics

and in the standard model of particle physics:

force field gauge bosons

scalar bosons

matter field fermions (spinors, Dirac fields)

flavors of fundamental fermions in the
standard model of particle physics:
generation of fermions1st generation2nd generation3d generation
quarks (qq)
up-typeup quark (uu)charm quark (cc)top quark (tt)
down-typedown quark (dd)strange quark (ss)bottom quark (bb)
leptons
chargedelectronmuontauon
neutralelectron neutrinomuon neutrinotau neutrino
bound states:
mesonslight mesons:
pion (udu d)
ρ-meson (udu d)
ω-meson (udu d)
f1-meson
a1-meson		strange-mesons:
ϕ-meson (ss¯s \bar s),
kaon, K*-meson (usu s, dsd s)
eta-meson (uu+dd+ssu u + d d + s s)

charmed heavy mesons:
D-meson (uc u c, dcd c, scs c)
J/ψ-meson (cc¯c \bar c)		bottom heavy mesons:
B-meson (qbq b)
ϒ-meson (bb¯b \bar b)
baryonsnucleons:
proton (uud)(u u d)
neutron (udd)(u d d)

(also: antiparticles)

effective particles

hadrons (bound states of the above quarks)

solitons

in grand unified theory

minimally extended supersymmetric standard model

superpartners

bosinos:

sfermions:

dark matter candidates

Exotica

auxiliary fields

Contents

Idea

In QCD a meson is a bound state of two quarks via the strong nuclear force.


flavors of fundamental fermions in the
standard model of particle physics:
generation of fermions1st generation2nd generation3d generation
quarks (qq)
up-typeup quark (uu)charm quark (cc)top quark (tt)
down-typedown quark (dd)strange quark (ss)bottom quark (bb)
leptons
chargedelectronmuontauon
neutralelectron neutrinomuon neutrinotau neutrino
bound states:
mesonslight mesons:
pion (udu d)
ρ-meson (udu d)
ω-meson (udu d)
f1-meson
a1-meson		strange-mesons:
ϕ-meson (ss¯s \bar s),
kaon, K*-meson (usu s, dsd s)
eta-meson (uu+dd+ssu u + d d + s s)

charmed heavy mesons:
D-meson (uc u c, dcd c, scs c)
J/ψ-meson (cc¯c \bar c)		bottom heavy mesons:
B-meson (qbq b)
ϒ-meson (bb¯b \bar b)
baryonsnucleons:
proton (uud)(u u d)
neutron (udd)(u d d)

Examples

First-generation mesons

The mesons in the first generation of fermions, being bound states of up quarks and down quarks are

As linear representations of the Lorentz group (or rather of thePin group) and isospin flavour group (under Wigner classification) these first-generation meson fields are given as in the first of the following two tables:

Here n\mathbf{n} denotes an irreducible representation of dimension nn, and the subscript sgn{}_{\mathrm{sgn}} indicates the one of the two irreps of that dimension which pick up an extra sign under orientation-reversal (4 sgn=4⊗1 sgn\mathbf{4}_{{}_{sgn}} = \mathbf{4} \otimes \mathbf{1}_{{}_{sgn}} for 1 sgn\mathbf{1}_{{}_{sgn}} the sign representation).

So the pion is a Lorentz-pseudoscalar, and the omega-meson and rho-meson are Lorentz pseudovector fields.

As bilinears in the up-quark Weyl spinor field uu and down-quark Weyl spinor field dd these meson fields are given as follows (with (σ 0,σ 1,σ 2,σ 3)(\sigma^0, \sigma^1, \sigma^2, \sigma^3) the Pauli matrices):

σ 0ω μ⏟omegameson+σ iρ i μ⏟rhomeson=(u¯γ μγ 5u u¯γ μγ 5d d¯γ μγ 5u d¯γ μγ 5d) \sigma^0 \underset{ {\color{blue}omega} \atop {\color{blue}meson} }{ \underbrace{ \omega^\mu } } + \sigma^i \underset{ {\color{blue}rho} \atop {\color{blue}meson} }{ \underbrace{ \rho^\mu_i } } \;=\; \left( \array{ \bar u \gamma^\mu \gamma^5 u & \bar u \gamma^\mu \gamma^5 d \\ \bar d \gamma^\mu \gamma^5 u & \bar d \gamma^\mu \gamma^5 d } \right)

Second-generation mesons

Mesons containing strange quarks (the first heavy mesons with respect to 2-flavor chiral perturbation theory) from the second generation of fermions:

Third-generation mesons

Heavy mesons containing bottom quarks from the second generation of fermions:

See also

Properties

Conceptualization and computation in AdS/QCD

In the Witten-Sakai-Sugimoto model for strongly coupled QCD via an intersecting D-brane model, the hadrons in QCD correspond to string-theoretic-phenomena in an ambient bulk field theory on an approximately anti de Sitter spacetime:

  1. the mesons (bound states of 2 quarks) correspond to open strings in the bulk, whose two endpoints on the asymptotic boundary correspond to the two quarks;

  2. baryons (bound states of N cN_c quarks) appear in two different but equivalent (Sugimoto 16, 15.4.1) guises:

    1. as wrapped D4-branes with N cN_c open strings connecting them to the D8-brane

      (Witten 98b, Gross-Ooguri 98)

    2. as skyrmions

      (Sakai-Sugimoto 04, section 5.2, Sakai-Sugimoto 05, section 3.3, see Bartolini 17).

For review see Sugimoto 16, also Rebhan 14, around (18).

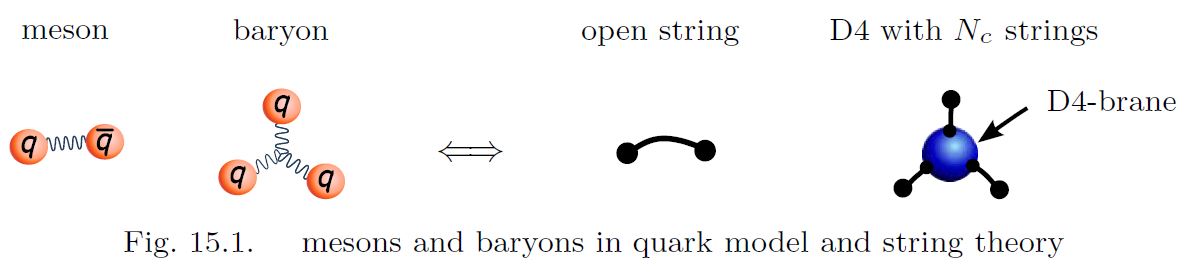
graphics grabbed from Sugimoto 16

This produces baryon mass spectra with moderate quantitative agreement with experiment (HSSY 07):

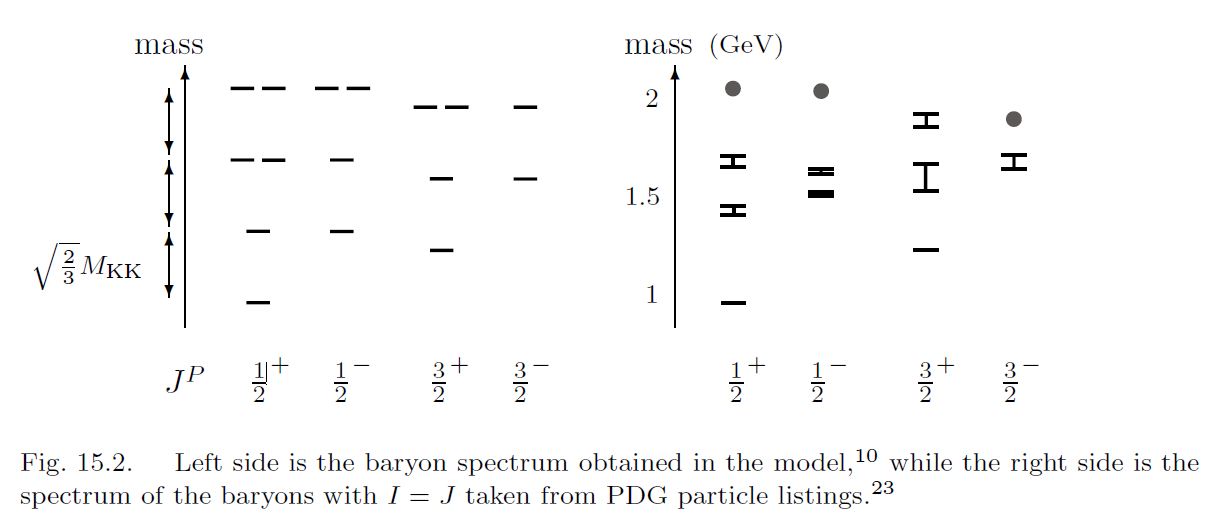
graphics grabbed from Sugimoto 16

References

General

  • Eef van Beveren, George Rupp, Scalar and axial-vector mesons, Eur. Phys. J. A31:468-473, 2007 (arXiv:hep-ph/0610199)

Origin of effective field theory of mesons in nuclear physics, via hidden local gauge symmetry:

Introduction and survey:

See also

The pole approximation?:

In chiral perturbation theory

See the references at chiral perturbation theory.

Walecka hadrodynamics with nucleon fields

On quantum hadrodynamics (relativivist effective field theory of nuclear physics, coupling mesons and nucleons) in the sense of the Walecka model, hence with nucleons appearing as explicit fields (as opposed to being solitonic Skyrmions in the pion field as in chiral perturbation theory).

Precursor:

The original Walecka model (QHD-I model), with nucleons coupled to sigma-mesons and omega-mesons:

Inclusion into the Walecka model also of the pion and the rho-meson (the QHD-II model):

Further discussion of these models:

Further inclusion of electromagnetism (photon field):

  • A. Yu. Korchin, D. Van Neck, M. Waroquier, Electromagnetic interaction in chiral quantum hadrodynamics and decay of vector and axial-vector mesons, Phys. Rev. C67 (2003) 015207 (arXiv:nucl-th/0302042)

Relation to quark-meson coupling model:

  • Koichi Saito, Relationship between Quark-Meson Coupling Model and Quantum Hadrodynamics, Prog. Theor. Phys. 108 (2002) 609-614 (arXiv:nucl-th/0207053)

Hadrodynamics via Light-front QCD

On light-front QCD for quantum hadrodynamics:

Skyrme hadrodynamics with vector mesons (π\pi-ω\omega-ρ\rho-model)

Inclusion of vector mesons (omega-meson and rho-meson/A1-meson) into the Skyrmion model of quantum hadrodynamics, in addition to the pion:

First, on the equivalence between hidden local symmetry- and massive Yang-Mills theory-description of Skyrmion quantum hadrodynamics:

  • Atsushi Hosaka, H. Toki, Wolfram Weise, Skyrme Solitons With Vector Mesons: Equivalence of the Massive Yang-Mills and Hidden Local Symmetry Scheme, 1988, Z. Phys. A332 (1989) 97-102 (spire:24079)

See also

  • Marcelo Ipinza, Patricio Salgado-Rebolledo, Meron-like topological solitons in massive Yang-Mills theory and the Skyrme model (arXiv:2005.04920)

Inclusion of the ω\omega-meson

Original proposal for inclusion of the ω-meson in the Skyrme model:

Relating to nucleon-scattering:

  • J. M. Eisenberg, A. Erell, R. R. Silbar, Nucleon-nucleon force in a skyrmion model stabilized by omega exchange, Phys. Rev. C 33, 1531 (1986) (doi:10.1103/PhysRevC.33.1531)

Combination of the omega-meson-stabilized Skyrme model with the bag model for nucleons:

Discussion of nucleon phenomenology for the ω\omega-stabilized Skyrme model:

Inclusion of the ρ\rho-meson

Original proposal for inclusion of the ρ-meson:

Discussion for phenomenology of light atomic nuclei:

See also:

Inclusion of the ω\omega- and ρ\rho-meson

The resulting π\pi-ρ\rho-ω\omega model:

See also

  • Ki-Hoon Hong, Ulugbek Yakhshiev, Hyun-Chul Kim, Modification of hyperon masses in nuclear matter, Phys. Rev. C 99, 035212 (2019) (arXiv:1806.06504)

Review:

Combination of the omega-rho-Skyrme model with the bag model of quark confinement:

  • H. Takashita, S. Yoro, H. Toki, Chiral bag plus skyrmion hybrid model with vector mesons for nucleon, Nuclear Physics A Volume 485, Issues 3–4, August 1988, Pages 589-605 (doi:10.1016/0375-9474(88)90555-6)

Inclusion of the σ\sigma-meson

Inclusion of the sigma-meson:

  • Thomas D. Cohen, Explicit σ\sigma meson, topology, and the large-NN limit of the Skyrmion, Phys. Rev. D 37 (1988) (doi:10.1103/PhysRevD.37.3344)

For analysis of neutron star equation of state:

  • David Alvarez-Castillo, Alexander Ayriyan, Gergely Gábor Barnaföldi, Hovik Grigorian, Péter Pósfay, Studying the parameters of the extended σ\sigma-ω\omega model for neutron star matter (arXiv:2006.03676)

Skyrme hadrodynamics with heavy quarks/mesons

Inclusion of heavy flavors into the Skyrme model for quantum hadrodynamics:

Inclusion of strange quarks/kaons

Inclusion of strange quarks/kaons into the Skyrme model:

Review:

Inclusion of charm quarks/D-mesons

Inclusion of charm quarks/D-mesons into the Skyrme model:

Inclusion of bottom quarks/B-mesons

Inclusion of further heavy flavors beyond strange quark/kaons, namely charm quarks/D-mesons and bottom quarks/B-mesons, into the Skyrme model:

  • Mannque Rho, D. O. Riska, Norberto Scoccola, The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages 343–352 (1992) (doi:10.1007/BF01283544)

  • Arshad Momen, Joseph Schechter, Anand Subbaraman, Heavy Quark Solitons: Strangeness and Symmetry Breaking, Phys. Rev. D49:5970-5978, 1994 (arXiv:hep-ph/9401209)

  • Yongseok Oh, Byung-Yoon Park, Dong-Pil Min, Heavy Baryons as Skyrmion with 1/m Q1/m_Q Corrections, Phys. Rev. D49 (1994) 4649-4658 (arXiv:hep-ph/9402205)

Review:

The WZW term of QCD chiral perturbation theory

The gauged WZW term of chiral perturbation theory/quantum hadrodynamics which reproduces the chiral anomaly of QCD in the effective field theory of mesons and Skyrmions:

General

The original articles:

See also:

  • O. Kaymakcalan, S. Rajeev, J. Schechter, Nonabelian Anomaly and Vector Meson Decays, Phys. Rev. D 30 (1984) 594 (spire:194756)

Corrections and streamlining of the computations:

  • Chou Kuang-chao, Guo Han-ying, Wu Ke, Song Xing-kang, On the gauge invariance and anomaly-free condition of the Wess-Zumino-Witten effective action, Physics Letters B Volume 134, Issues 1–2, 5 January 1984, Pages 67-69 (doi:10.1016/0370-2693(84)90986-9))

  • H. Kawai, S.-H. H. Tye, Chiral anomalies, effective lagrangians and differential geometry, Physics Letters B Volume 140, Issues 5–6, 14 June 1984, Pages 403-407 (doi:10.1016/0370-2693(84)90780-9)

  • J. L. Mañes, Differential geometric construction of the gauged Wess-Zumino action, Nuclear Physics B Volume 250, Issues 1–4, 1985, Pages 369-384 (doi:10.1016/0550-3213(85)90487-0)

  • Tomáš Brauner, Helena Kolešová, Gauged Wess-Zumino terms for a general coset space, Nuclear Physics B Volume 945, August 2019, 114676 (doi:10.1016/j.nuclphysb.2019.114676)

See also

Interpretation as Skyrmion/baryon current:

Concrete form for NN-flavor quantum hadrodynamics in 2d:

  • C. R. Lee, H. C. Yen, A Derivation of The Wess-Zumino-Witten Action from Chiral Anomaly Using Homotopy Operators, Chinese Journal of Physics, Vol 23 No. 1 (1985) (spire:16389, pdf)

Concrete form for 2 flavors in 4d:

  • Masashi Wakamatsu, On the electromagnetic hadron current derived from the gauged Wess-Zumino-Witten action, (arXiv:1108.1236, spire:922302)

Including light vector mesons

Concrete form for 2-flavor quantum hadrodynamics in 4d with light vector mesons included (omega-meson and rho-meson):

Including heavy scalar mesons

Including heavy scalar mesons:

specifically kaons:

specifically D-mesons:

(…)

specifically B-mesons:

  • Mannque Rho, D. O. Riska, N. N. Scoccola, above (2.1) in: The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages343–352 (1992) (doi:10.1007/BF01283544)

Including heavy vector mesons

Inclusion of heavy vector mesons:

specifically K*-mesons:

Including electroweak interactions

Including electroweak fields:

Discussion for the full standard model of particle physics:

  • Jeffrey Harvey, Christopher T. Hill, Richard J. Hill, Standard Model Gauging of the WZW Term: Anomalies, Global Currents and pseudo-Chern-Simons Interactions, Phys. Rev. D77:085017, 2008 (arXiv:0712.1230)

Hadrons as KK-modes of 5d Yang-Mills theory

The suggestion that the tower of observed vector mesons – when regarded as gauge fields of hidden local symmetries of chiral perturbation theory – is reasonably modeled as a Kaluza-Klein tower of D=5 Yang-Mills theory:

That the pure pion-Skyrmion-model of baryons is approximately the KK-reduction of instantons in D=5 Yang-Mills theory is already due to:

with a hyperbolic space-variant in:

Further discussion of this approximation:

The observation that the result of Atiyah-Manton 89 becomes an exact Kaluza-Klein construction of Skyrmions/baryons from D=5 instantons when the full KK-tower of vector mesons as in Son-Stephanov 03 is included into the Skyrmion model (see also there) is due to:

In the Sakai-Sugimoto model of holographic QCD the D=5 Yang-Mills theory of this hadron Kaluza-Klein theory is identified with the worldvolume-theory of D8-flavour branes intersected with D4-branes in an intersecting D-brane model:

Extensive review of this holographic/KK-theoretic-realization of quantum hadrodynamics from D=5 Yang-Mills theory is in:

Via the realization of D4/D8 brane bound states as instantons in the D8-brane worldvolume-theory (see there and there), this relates also to the model of baryons as wrapped D4-branes, originally due to

and further developed in the nuclear matrix model:

In relation to Yang-Mills monopoles:

Discussion, in this context, of D-term effects affecting hadron stability:

More on baryons in the Sakai-Sugimoto model of holographic QCD:

More on mesons in holographic QCD:

An alternative scenario of derivation of 4d Skyrmions by KK-compactification of D=5 Yang-Mills theory, now on a closed interval, motivated by M5-branes instead of by D4/D8-brane intersections as in the Sakai-Sugimoto model, is discussed in:

with related discussion in:

See also:

  • Y. H. Ahn, Sin Kyu Kang, Hyun Min Lee, Towards a Model of Quarks and Leptons (arXiv:2112.13392)

In the large NN limit

In the large N limit:

Last revised on December 28, 2023 at 11:59:40. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (45 revisions) Cite Print Source