Ѕвездено пулсирање

Светлинска крива на променливата ѕвезда од типот на Делта Кефеј, покажувајќи ја правилната светлинска крива образувана од внатрешните ѕвездени пулсирања.

Ѕвездените пулсирања се предизвикани од проширувања и контракции во надворешните слоеви додека ѕвездата се обидува да одржи рамнотежа. Овие флуктуации во ѕвездениот полупречник предизвикуваат соодветни промени во сјајноста на ѕвездата. Астрономите можат да го заклучат овој механизам со мерење на спектарот и набљудување на Доплеровиот ефект. Многу внатрешнопроменливи ѕвезди кои пулсираат со големи замави, како што се класичните Кефеиди, ѕвездите од типот на RR Лира и ѕвездите од типот на Делта Штит со голем замав, покажуваат правилни светлински криви.

Ова редовно однесување е во спротивност со променливоста на ѕвездите кои лежат напоредно и со страната со висока сјајност/ниска температура на класичните променливи ѕвезди во Херцшрунг-Раселовиот дијаграм. Забележано е дека овие џиновски ѕвезди подлежат на пулсирања кои се движат од слаба неправилност, кога сè уште може да биде дефинирано просечно време или кружен период, (како во повеќето ѕвезди од типот на RV Бик и полуправилни променливи ѕвезди) до речиси отсуство на повторливост кај неправилните променливи ѕвезди. Променливите ѕвезди W Девица се во средина; кратките периоди се правилни, а подолгите покажуваат први релативно редовни алтернации во циклусите на пулсирања, проследени со појава на благи неправилности како кај ѕвездите од типот на RV Бик во кои тие постепено се претвораат како што нивните периоди стануваат подолги. Теориите за еволуција и пулсирање на ѕвездите наведуваат дека овие неправилни ѕвезди имаат многу поголем сооднос на сјајност и маса (с/м).

Многу ѕвезди се нерадијални пулсатори, кои имаат помали флуктуации во осветленоста од оние на обичните променливи што биле користени како точки показатели.

Правилни променливи ѕвезди

Предуслов за неправилна променливост е ѕвездата да може да го промени својот замав на временската скала на еден период. Со други зборови, спојката помеѓу пулсирањето и протокот на топлина мора да биде доволно голема за да дозволи такви промени. Оваа спојка се мери со релативната линеарна стапка на раст или распаѓање κ (капа) на замавот на дадено нормално колебање во еден циклус на пулсирање (период). За редовните променливи ѕвезди (Кефеиди, RR Лира, итн.), бројчаното ѕвездено моделирање и анализата на линеарната стабилност покажуваат дека κ е најмногу од редот на неколку проценти за релевантните, возбудени пулсирачки колебања. Од друга страна, истиот тип на анализа покажува дека за моделите со висока с/м το κ е значително поголем (30% или повеќе).

За редовните променливи малите релативни стапки на раст κ, имплицираат дека постојат две различни временски скали, имено периодот на колебање и подолгото време поврзано со варијацијата на замавот. Математички гледано, динамиката има централен собирач, или поточно блиску средишен собирач. Дополнително, откриено е дека ѕвездените пулсирања се само слабо нелинеарни во смисла дека нивниот опис може да биде ограничена моќност на замавите на пулсирањето. Овие две својства се многу општи и се појавуваат за колебливите системи во многу други области како што се динамиката на населението, океанографијата, физиката на плазмата итн.

Слабата нелинеарност и долгата временска скала на варијацијата на замавот овозможува временскиот опис на пулсирачкиот систем да биде поедноставен на оној на само пулсирачките замави, со што е елиминирано движењето на кратката временска скала на периодот. Резултатот е опис на системот во однос на замавните равенки кои се скратени на малите сили на замавите. Ваквите замавни равенки биле изведувани со различни техники, на пр. Поанкаре-Линдштетовиот метод за елиминација на неврзаните поими или методот на повеќекратна асимптотична пертурбација, и поопшто, теоријата на нормален облик.

На пример, во случај на два нерезонантни колебања, ситуација која воглавно се среќава во променливите ѕвезди од типот на RR Лира, временската еволуција на замавите A₁ и A₂ од двата нормални колебања 1 и 2 е регулирана со следново множество обични диференцијални равенки $${\begin{aligned}{\frac {dA_{1}}{dt}}&=\kappa _{1}A_{1}+\left(Q_{11}A_{1}^{2}+Q_{12}A_{2}^{2}\right)A_{1}\\[1ex]{\frac {dA_{2}}{dt}}&=\kappa _{2}A_{2}+\left(Q_{21}A_{1}^{2}+Q_{22}A_{2}^{2}\right)A_{2}\end{aligned}}$$ каде што Q _ij се нерезонантните коефициенти на спојување.

Овие замавни равенки се ограничени на нетривијални нелинеарности од најнизок ред. Решенијата од интерес во теоријата на ѕвездената пулсација се асимптотичните решенија (како времето се стреми кон бесконечноста), бидејќи временската скала за варијациите на замавот е воглавно многу кратка во споредба со временската скала на еволуцијата на ѕвездата, која е временска скала на горење на јадрото. Равенките погоре имаат решенија со неподвижна точка со постојани замави, што одговараат на единечно колебање (A₁ $\neq$ 0, A₂ = 0) или (A₁ = 0, A₂ $\neq$ 0) и решенија со двојно колебање (A₁ $\neq$ 0, А₂ $\neq$ 0). Тие одговараат на поединечни периодични и двојно периодични пулсирања на ѕвездата. Не постои друго асимптотичко решение на горенаведените равенки за физички (т.е. негативни) коефициенти на спојување.

За резонантните колебања, соодветните замавни равенки имаат дополнителни поими кои ја опишуваат резонантната спојка меѓу колебањата. Херцшпрунговото напредување во морфологијата на светлинската крива на класичните (поединечно периодични) Кефеиди е резултат на добро познатата резонанца 2:1 меѓу основното колебање на пулсирање и второто призвучно колебање. Равенката на замавот може дополнително да биде проширена на нерадијални ѕвездени пулсирања.

Во севкупната анализа на пулсирачките ѕвезди, замавните равенки овозможуваат да биде картиран дијаграмот на бифуркација помеѓу можните пулсирачки состојби. На оваа слика, границите на лентата на нестабилност каде што се појавува пулсирањето за време на еволуцијата на ѕвездата одговараат на Хопфовата бифуркација.

Постоењето на средиштен собирач ја елиминира можноста за хаотични (т.е. неправилни) пулсирања на временската скала на периодот. Иако равенките на резонантниот замав се доволно сложени за да овозможат и хаотични решенија, ова е многу различен хаос бидејќи е во временската варијација на замавите и се јавува на долг временски размер.

Додека долгорочното неправилно однесување во временските варијации на замавите на пулсирањето е можно кога се применувани замавните равенки, ова не е општата ситуација. Навистина, за поголемиот дел од набљудувањата и моделирањето, пулсирањата на овие ѕвезди се случуваат со постојани Фурјеови замави, што доведува до редовни пулсирања кои можат да бидат периодични или повеќепериодични (квазипериодични во математичката книжевност).

Неправилни пулсирања

Светлинските криви на внатрешнопроменливите ѕвезди со големи замависо векови се познати по тоа што покажуваат однесување кое оди од крајна регуларност, како за класичните Кефеиди и ѕвездите од типот на RR Лира, до крајна неправилност, како и за таканаречените неправилни променливи. Кај ѕвездите од население II оваа неправилност постепено се зголемува од нископериодичните променливи ѕвезди од типот на W Девица преку променливите ѕвезди од типот на RV Бик во колебањето на полуправилните променливи. Нискодимензионалниот хаос во ѕвездените пулсирања е моменталното толкување на овој воспоставен феномен.

Правилно однесување на Кефеидите

Правилното однесување на Кефеидите е успешно моделирано со бројчана хидродинамика уште од 1960-тите, и од теоретска гледна точка лесно е разбирливо како резултат на присуството на средиштен собирач кој се јавува поради слабо дисипативната природа на динамичкиот систем. Ова, и фактот што пулсирањата се слабо нелинеарни, овозможува опис на системот во однос на замавните равенките и конструкција на дијаграмот на бифуркација (видиете исто така теорија на бифуркација) на можните типови на пулсирање (или гранични циклуси), како пулсирање на основното колебање, пулсирање на првиот или вториот призвук или посложени пулсирања со двојно колебање во кои неколку колебања се возбудени со постојани замави. Границите на појасот на нестабилност каде што доаѓа до пулсирање за време на еволуцијата на ѕвездата одговараат на Хопфовата бифуркација.

Неправилни ѕвезди од населението II

Спротивно на тоа, неправилноста на ѕвездите од населението II кои се со голем замав, е поголем предизвик за да биде објаснет. Варијацијата на замавот на пулсирање во текот на еден период подразбира голема дисипација, и затоа не постои средишен собирач. Различни механизми се предложени, но било утврдено дека недостасуваат. Едниот, наведува присуство на неколку тесно распоредени честоти на пулсирање кои би се тепале една против друга, но такви честоти не постојат во соодветните ѕвездени модели. Друг, поинтересен предлог е дека варијациите се од стохастичка природа, но не бил предложен или не постои механизам кој би можел да обезбеди енергија за такви големи набљудувани варијации на замавот. Сега е утврдено дека механизмот зад неправилните светлински криви е основната нискодимензионална хаотична динамика (видете исто така теорија на хаос). Овој заклучок се заснова на два вида студии.

Симулации на сметачка динамика на флуиди

Бројчаните прогнози за сметачката динамиката на флуиди за пулсирањата на низите на ѕвездените модели на W Девица покажуваат два пристапи кон неправилно однесување кои се јасен потпис на нискодимензионалниот хаос. Првото покажување доаѓа од „првите карти за враќање“ во кои е исцртуван еден максимален полупречник, или која било друга соодветна променлива ѕвезда, наспроти следната. Редоследот на модели покажува период кој удвојува бифуркација, или каскада, што доведува до хаос. Скоро квадратниот облик на картата е показател за хаос и имплицира потковичеста карта. Други низи на модели следат малку поинаков пат, но исто така и до хаос, имено Помео-Маневиловата или тангентна бифуркациска рута.

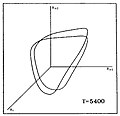
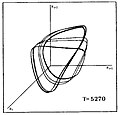
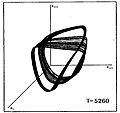
Следното покажува слична согледување на периодот на удвојување на каскадата до хаос за низа од ѕвездени модели кои се разликуваат според нивната просечна површинска температура Т. Графикот покажува тројки вредности на ѕвездениот полупречник (R_i, R_i+1, R_{i+ 2}) каде што индексите _i, _i+1, _i+2 означуваат последователни временски интервали.

P0	P2	P4	P8	Поврзан хаос	Целосен хаос

Присуството на нискодимензионален хаос е потврдено и со друга, пософистицирана анализа на моделските пулсирања која ги извлекува најниските нестабилни периодични орбити и ја испитува нивната тополошка организација (извртување). Откриено е дека основниот привлекувач е обвиткан како Реслеровиот привлекувач, но сепак има дополнителен пресврт во лентата.

Општа реконструкција на протокот од набљудуваните светлински криви

Методот на општа реконструкција на протокот користи единствен набљудуван сигнал {s_i} за да заклучи својства на динамичкиот систем што го создал. Први N-димензионални „вектори“ $S_{i}=s_{i},s_{i-1},s_{i-2},...s_{i-N+1}$ се конструирани. Следниот чекор се состои во наоѓање израз за нелинеарниот еволуциски оператор $M$ што го одзема системот од времето $i$ на времето $i+1$ т.е. $S_{i+1}=M(S_{i})$. Такенсовата теорема гарантира дека во многу општи околности тополошките својства на овој реконструиран оператор на еволуција се исти како оние на физичкиот систем, под услов димензијата на вградување N да биде доволно голема. Така , „од знаењето за една набљудувана променлива ѕвезда“ може да бидат заклучени својствата за вистинскиот физички систем кој е управуван од голем број независни променливи ѕвезди.

Овој пристап е применет на податоците на Американското здружение на набљудувачи на променливи ѕвезди (АЗНПЅ), за ѕвездата R Штит. Може да биде заклучено дека неправилните пулсирања на оваа ѕвезда произлегуваат од основната четиридимензионална динамика. Различно фразирано, ова вели дека од било кои 4 соседни набљудувања може да биде предвидено следното. Од физичка гледна точка вели дека има 4 независни променливи ѕвезди кои ја опишуваат динамиката на системот. Методот на лажни најблиски соседи ја потврдува димензијата на вградување од 4. Фракталната димензија на динамиката на R Штит како што е заклучувано од пресметаните Љапунови експоненти лежи помеѓу 3,1 и 3,2.

Горе: R Штит забележана светлинска крива од страна на АЗНПЅ (измазнета); Долу: Синтетичка светлинска крива, добиена со помош на реконструираниот оператор на еволуција. Забележете ја сличноста со набљудуваната светлинската крива.

Од анализата на неподвижните точки на операторот на еволуција може да биде заклучено убава физичка слика, имено дека „пулсирањата произлегуваат од возбудувањето на нестабилно пулсирачко колебање кој нелинеарно се поврзува со вториот, стабилно пулсирачко колебање кое е во резонанца 2:1 со првото“, сценарио опишано со Шилниковата теорема.

Овој механизам за резонанца не е ограничен само на R Штит, туку е откриено дека важи и за неколку други ѕвезди за кои податоците од набљудувањето се доволно добри.

Поврзано

• Астеросеизмологија
• Хибриден пулсатор
• Пулсирачко бело џуџе
• Пулсар