Decoy-state round-robin differential-phase-shift quantum key distribution with source errors

Abstract

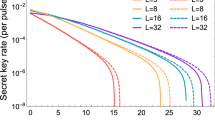
As a promising quantum key distribution (QKD), most of the existing round-robin differential-phase-shift quantum key distribution (RRDPS-QKD) protocols have adopted the decoy-state method and have assumed the source states are exactly controlled. However, the precise manipulation of source states is impossible for any practical experiment, and the RRDPS-QKD with source errors has an unignorable impact on the performance of the protocol. In the paper, we study the four-intensity decoy-state RRDPS-QKD protocol with source errors, formulate the secure generation key rate of the proposed protocol, and do the numerical simulations to testify the deductions. The results show that our evaluation can estimate the influence of source errors.

Appendix

In this section, we will give the lower bounds of $D_0$, $D_1$, $D_2$.

In order to get the lower bound of $D_0$, applying $p_{1,\nu _1 }^L$ Eq. (9) $-p_{1,\nu _2 }^U$ Eq. (8), we have

$$\begin{aligned}&p_{1,\nu _1 }^L\frac{{N_{\nu _2 } }}{{P_{\nu _2 } }} - p_{1,\nu _2 }^U \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }} \nonumber \\&\quad = \sum \limits _{i \in c_0 } {\left( {p_{1,\nu _1 }^L p_{0i,\nu _2 } - p_{1,\nu _2 }^U p_{0i,\nu _1 } } \right) d_{0i} } + \sum \limits _{i \in c_1 } {\left( {p_{1,\nu _1 }^L p_{1i,\nu _2 } - p_{1,\nu _2 }^U p_{1i,\nu _1 } } \right) d_{1i} } \nonumber \\&\qquad + \sum \limits _{k = 2}^J {\sum \limits _{i \in c_k } {\left( {p_{1,\nu _1 }^L p_{ki,\nu _2 } - p_{1,\nu _2 }^U p_{ki,\nu _1 } } \right) d_{ki} } } \nonumber \\&\quad \le \sum \limits _{i \in c_0 } {\left( {p_{1,\nu _1 }^L p_{0,\nu _2 }^U - p_{1,\nu _2 }^U p_{0,\nu _1 }^L } \right) d_{0i} } + \sum \limits _{i \in c_1 } {\left( {p_{1,\nu _1 }^L p_{1,\nu _2 }^U - p_{1,\nu _2 }^U p_{1,\nu _1 }^L } \right) d_{1i} } \nonumber \\&\qquad + \sum \limits _{k = 2}^J {\sum \limits _{i \in c_k } {\left( {p_{1,\nu _1 }^L p_{k,\nu _2 }^U - p_{1,\nu _2 }^U p_{k,\nu _1 }^L } \right) d_{ki} } } \nonumber \\&\quad =\left( {p_{1,\nu _1 }^L p_{0,\nu _2 }^U - p_{1,\nu _2 }^U p_{0,\nu _1 }^L } \right) \sum \limits _{i \in c_0 } {d_{0i} }+ \sum \limits _{k = 2}^J \left( {p_{1,\nu _1 }^L p_{k,\nu _2 }^U - p_{1,\nu _2 }^U p_{k,\nu _1 }^L } \right) {\sum \limits _{i \in c_k } {d_{ki} } }. \end{aligned}$$

(21)

According to the definitions of $D_0$, $D_1$ and $D_2$, we get

$$\begin{aligned}&p_{1,\nu _1 }^L\frac{{N_{\nu _2 } }}{{P_{\nu _2 } }} - p_{1,\nu _2 }^U \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }} \nonumber \\&\quad \le \left( {p_{1,\nu _1 }^L p_{0,\nu _2 }^U - p_{1,\nu _2 }^U p_{0,\nu _1 }^L } \right) D_0+\sum \limits _{k = 2}^J \left( {p_{1,\nu _1 }^L p_{k,\nu _2 }^U - p_{1,\nu _2 }^U p_{k,\nu _1 }^L } \right) {D_k}. \end{aligned}$$

(22)

Due to the conditions of Eq.(15), we can obtain an inequality $p_{1,\nu _1 }^L p_{k,\nu _2 }^U - p_{1,\nu _2 }^U p_{k,\nu _1 }^L \le 0 \quad for\;all\;k \ge 2$. Therefore, the inequality in Eq.(22) becomes

$$\begin{aligned} p_{1,\nu _1 }^L\frac{{N_{\nu _2 } }}{{P_{\nu _2 } }} - p_{1,\nu _2 }^U \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }} \le \left( {p_{1,\nu _1 }^L p_{0,\nu _2 }^U - p_{1,\nu _2 }^U p_{0,\nu _1 }^L } \right) D_0 , \end{aligned}$$

(23)

and the lower bound of $D_0$ is obtained by

$$\begin{aligned} D_0 \ge D_0^L = \max \left\{ {\frac{{p_{1,\nu _1 }^L \frac{{N_{\nu _2 } }}{{P_{\nu _2 } }} - p_{1,\nu _2 }^U \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }}}}{{p_{1,\nu _1 }^L p_{0,\nu _2 }^U - p_{1,\nu _2 }^U p_{0,\nu _1 }^L }},\,0} \right\} . \end{aligned}$$

(24)

Then, similar to Eq.(21), by $p_{0,\nu _2 }^L$ Eq. (8) $-p_{0,\nu _1 }^U$ Eq. (9), we have

$$\begin{aligned}&p_{0,\nu _2 }^L \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }} - p_{0,\nu _1 }^U \frac{{N_{\nu _2 } }}{{P_{\nu _2 } }} \nonumber \\&\quad \le (p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )D_1 + \sum \limits _{k = 2}^J {\sum \limits _{i \in c_k } {(p_{0,\nu _2 }^L p_{k,\nu _1 }^U - p_{0,\nu _1 }^U p_{k,\nu _2 }^L )d_{ki} } } \nonumber \\&\quad \le (p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )D_1+ \sum \limits _{k = 2}^J \frac{p_{0,\nu _2 }^L p_{k,\nu _1 }^U - p_{0,\nu _1 }^U p_{k,\nu _2 }^L }{{p_{k,\mu }^L }} {\sum \limits _{i \in c_k } {d_{ki} p_{ki,\mu } } } \nonumber \\&\quad \le (p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )D_1 + \frac{p_{0,\nu _2 }^L p_{2,\nu _1 }^U - p_{0,\nu _1 }^U p_{2,\nu _2 }^L }{{p_{2,\mu }^L }}[\frac{{N_\mu }}{{P_\mu }} - p_{0,\mu }^L D_0^L - p_{1,\mu }^L D_1 ]. \end{aligned}$$

(25)

Here, the inequality that $\frac{(p_{0,\nu _2 }^L p_{k,\nu _1 }^U - p_{0,\nu _1 }^U p_{k,\nu _2 }^L )}{{p_{k,\mu }^L }} \le \frac{(p_{0,\nu _2 }^L p_{2,\nu _1 }^U - p_{0,\nu _1 }^U p_{2,\nu _2 }^L )}{{p_{2,\mu }^L }}$ for $k \ge 2$ is adopted to prove the inequality in Eq.(25). Consequently, the lower bound of $D_1$ can be estimated by

$$\begin{aligned} D_1 \ge D_1^L = \frac{{(p_{0,\nu _2 }^L \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }} - p_{0,\nu _1 }^U \frac{{N_{\nu _2 } }}{{P_{\nu _2 } }})p_{2,\mu }^L - (p_{0,\nu _2 }^L p_{2,\nu _1 }^U - p_{0,\nu _1 }^U p_{2,\nu _2 }^L )(\frac{{N_\mu }}{{P_\mu }} - p_{0,\mu }^L D_0^L )}}{{(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )p_{2,\mu }^L - (p_{0,\nu _2 }^L p_{2,\nu _1 }^U - p_{0,\nu _1 }^U p_{2,\nu _2 }^L )p_{1,\mu }^L }}, \end{aligned}$$

(26)

where $D_0^L$ has been calculated in Eq.(24).

Combining the two equations [$p_{0,\nu _2}^L$ Eq. (8)$-p_{0,\nu _1}^U$ Eq. (9) ] and [$p_{0,\nu _3}^U$ Eq. (9)$-p_{0,\nu _2 }^L$ Eq. (10)], we can have

$$\begin{aligned}&(p_{0,\nu _2 }^L \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }} - p_{0,\nu _1 }^U \frac{{N_{\nu _2 } }}{{P_{\nu _2 } }})(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U \frac{{N_{\nu _2 } }}{{P_{\nu _2 } }} - p_{0,\nu _2 }^L \frac{{N_{\nu _3 } }}{{P_{\nu _3 } }})(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L ) \nonumber \\&\quad \le [(p_{0,\nu _2 }^L p_{2,\nu _1 }^U - p_{0,\nu _1 }^U p_{2,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U p_{2,\nu _2 }^L - p_{0,\nu _2 }^L p_{2,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )]D_2 \nonumber \\&\qquad + \sum \limits _{k = 3}^J \frac{{(p_{0,\nu _2 }^L p_{k,\nu _1 }^U - p_{0,\nu _1 }^U p_{k,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U p_{k,\nu _2 }^L - p_{0,\nu _2 }^L p_{k,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )}}{{p_{k,\mu }^L }}\nonumber \\&\quad \qquad \times {\sum \limits _{i \in c_k } {p_{ki,\mu } d_{ki} } } \nonumber \\&\quad \le [(p_{0,\nu _2 }^L p_{2,\nu _1 }^U - p_{0,\nu _1 }^U p_{2,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U p_{2,\nu _2 }^L - p_{0,\nu _2 }^L p_{2,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )]D_2 \nonumber \\&\qquad + \frac{{(p_{0,\nu _2 }^L p_{3,\nu _1 }^U - p_{0,\nu _1 }^U p_{3,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U p_{3,\nu _2 }^L - p_{0,\nu _2 }^L p_{3,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )}}{{p_{3,\mu }^L }} \nonumber \\&\quad \cdot (\frac{{N_\mu }}{{P_\mu }} - p_{0,\mu }^L D_0^L - p_{1,\mu }^L D_1^L - p_{2,\mu }^L D_2 ), \end{aligned}$$

(27)

where the inequality is due to $\frac{{(p_{0,\nu _2 }^L p_{k,\nu _1 }^U - p_{0,\nu _1 }^U p_{k,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U p_{k,\nu _2 }^L - p_{0,\nu _2 }^L p_{k,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )}}{{p_{k,\mu }^L }} \le \frac{{(p_{0,\nu _2 }^L p_{3,\nu _1 }^U - p_{0,\nu _1 }^U p_{3,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U p_{3,\nu _2 }^L - p_{0,\nu _2 }^L p_{3,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )}}{{p_{3,\mu }^L }}$ for $k\ge 3$.

Hence, the lower bound of $D_2$ can be expressed by

$$\begin{aligned}&D_2\ge D_2^L \nonumber \\&\quad = \bigg \{\bigg [(p_{0,\nu _2 }^L \frac{{N_{\nu _1 } }}{{P_{\nu _1 } }} - p_{0,\nu _1 }^U \frac{{N_{\nu _2 } }}{{P_{\nu _2 } }})(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U \frac{{N_{\nu _2 } }}{{P_{\nu _2 } }} - p_{0,\nu _2 }^L \frac{{N_{\nu _3 } }}{{P_{\nu _3 } }})(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )\bigg ]p_{3,\mu }^L \nonumber \\&\qquad -\bigg [(p_{0,\nu _2 }^L p_{3,\nu _1 }^U - p_{0,\nu _1 }^U p_{3,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) - (p_{0,\nu _3 }^U p_{3,\nu _2 }^L - p_{0,\nu _2 }^L p_{3,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )\bigg ] \nonumber \\&\quad (\frac{{N_\mu }}{{P_\mu }} - p_{0,\mu }^L D_0^L - p_{1,\mu }^L D_1^L ) \bigg \} \bigg / \bigg \{ \bigg [(p_{0,\nu _2 }^L p_{2,\nu _1 }^U - p_{0,\nu _1 }^U p_{2,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) \nonumber \\&\qquad - (p_{0,\nu _3 }^U p_{2,\nu _2 }^L - p_{0,\nu _2 }^L p_{2,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U \nonumber \\&\qquad - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )\bigg ] p_{3,\mu }^L- \bigg [(p_{0,\nu _2 }^L p_{3,\nu _1 }^U - p_{0,\nu _1 }^U p_{3,\nu _2 }^L )(p_{0,\nu _3 }^U p_{1,\nu _2 }^L - p_{0,\nu _2 }^L p_{1,\nu _3 }^U ) \nonumber \\&\qquad - (p_{0,\nu _3 }^U p_{3,\nu _2 }^L - p_{0,\nu _2 }^L p_{3,\nu _3 }^U )(p_{0,\nu _2 }^L p_{1,\nu _1 }^U - p_{0,\nu _1 }^U p_{1,\nu _2 }^L )\bigg ] p_{2,\mu }^L \bigg \}. \end{aligned}$$

(28)