Bijective Rigid Motions of the 2D Cartesian Grid

Abstract

Rigid motions are fundamental operations in image processing. While they are bijective and isometric in $\mathbb {R}^2$, they lose these properties when digitized in $\mathbb {Z}^2$. To investigate these defects, we first extend a combinatorial model of the local behavior of rigid motions on $\mathbb {Z}^2$, initially proposed by Nouvel and Rémila for rotations on $\mathbb {Z}^2$. This allows us to study bijective rigid motions on $\mathbb {Z}^2$, and to propose two algorithms for verifying whether a given rigid motion restricted to a given finite subset of $\mathbb {Z}^2$ is bijective.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Rigid motions (i.e., rotations, translations and their compositions) defined on $\mathbb {Z}^2$ are simple yet crucial operations in many image processing applications involving 2D data. One way to design rigid motions on $\mathbb {Z}^2$ is to combine continuous rigid motions defined on $\mathbb {R}^2$ with a digitization operator that maps the results back into $\mathbb {Z}^2$. However, the digitized rigid motion, though uniformly “close” to its continuous origin, often no longer satisfies the same properties. In particular, bijectivity is lost in general. In this context, it is useful to understand the combinatorial, geometrical and topological alterations associated with digitized rigid motions. More precisely, we observe the impact of rigid motions on the structure of $\mathbb {Z}^2$ at a local scale. Few efforts were already devoted to such topic, in particular for digitized rotations. Especially, pioneering works by Nouvel and Rémila [6] led to an approach for characterizing bijective digitized rotations [7], and more generally studying non-bijective ones [8].

Our contribution is threefold. We first show the usefulness of a combinatorial model of the local behavior of rigid motions on $\mathbb {Z}^2$, proposed initially for rotations on $\mathbb {Z}^2$ [6, 8], called neighborhood motion maps. By using this model, we characterize bijective rigid motions on $\mathbb {Z}^2$, similarly to the characterization of bijective digitized rotations [7]. As such characterization is made locally, we also show that the local bijectivity of rigid motions on $\mathbb {Z}^2$, i.e. bijectivity of rigid motions of finite sets on $\mathbb {Z}^2$, can be verified by using neighborhood motion maps.

This article is organized as follows. In Sect. 2 we recall basic definitions and generalize to digitized rigid motions on $\mathbb {Z}^2$ the combinatorial model proposed previously by Nouvel and Rémila for rotations on $\mathbb {Z}^2$ [6, 8]. Section 3 provides a characterization of bijective rigid motions on $\mathbb {Z}^2$; this characterization is an extension of the one proposed in [7]. In Sect. 4 we provide new algorithms for the verification whether a given rigid motion is bijective or not when restricted to a finite subset of $\mathbb {Z}^2$. Finally, in Sect. 5 we conclude this article and provide some perspectives.

2 Basic Notions

2.1 Digitized Rigid Motions

Rigid motions on $\mathbb {R}^2$ are bijective isometric maps defined as

$$\begin{aligned} \left| \begin{array}{lllll} \mathcal {U}&{} : &{} \mathbb {R}^2 &{} \rightarrow &{} \mathbb {R}^2 \\ &{} &{} \mathbf {x}&{} \mapsto &{} \mathbf {R}\mathbf {x}+ \mathbf {t}\end{array} \right. \end{aligned}$$

(1)

where $\mathbf {t}= (t_x,t_y)^t \in \mathbb {R}^2$ is a translation vector and $\mathbf {R}$ is a rotation matrix with $\theta \in [0,2\pi )$ its rotation angle. This leads to the representation of rigid motions by a triple of parameters $(\theta , t_x, t_y) \in [0,2\pi ) \times \mathbb {R}^2$.

According to Eq. (1), we generally have $\mathcal {U}(\mathbb {Z}^2) \nsubseteq \mathbb {Z}^2$. As a consequence, in order to define digitized rigid motions as maps from $\mathbb {Z}^2$ to $\mathbb {Z}^2$, we commonly apply rigid motions on $\mathbb {Z}^2$ as a part of $\mathbb {R}^2$, and then combine the real results with a digitization operator

$$\begin{aligned} \left| \begin{array}{lllll} \mathcal {D}&{} : &{} \mathbb {R}^2 &{} \rightarrow &{} \mathbb {Z}^2 \\ &{} &{} (x,y) &{} \mapsto &{} \left( \left\lfloor x + \frac{1}{2} \right\rfloor , \left\lfloor y + \frac{1}{2} \right\rfloor \right) \end{array} \right. \end{aligned}$$

(2)

where $\lfloor z \rfloor$ denotes the largest integer not greater than z. Digitized rigid motions are then defined as $U = \mathcal {D}\circ \mathcal {U}_{\mid \mathbb {Z}^2}$. Due to the behavior of $\mathcal {D}$ that maps $\mathbb {R}^2$ onto $\mathbb {Z}^2$, digitized rigid motions are, most of the time, non-bijective. This leads us to define a notion of point status with respect to digitized rigid motions [5].

Definition 1

Let $\mathbf {y}\in \mathbb {Z}^2$ be an integer point. The set of preimages of $\mathbf {y}$ with respect to U is defined as $S_U(\mathbf {y}) = \{ \mathbf {x}\in \mathbb {Z}^2 \mid U(\mathbf {x}) = \mathbf {y}\}$, and $\mathbf {y}$ is referred to as a s-point, where $s = |S_U(\mathbf {y})|$ is called the status of $\mathbf {y}$.

Remark 1

In $\mathbb {Z}^2$, $|S_U(\mathbf {y})| \in \{0,1,2\}$ and only points $\mathbf {p}$ and $\mathbf {q}$ such that $|\mathbf {p}- \mathbf {q}| = 1$ can be preimages of a 2-point [3].

The non-injective and non-surjective behaviors of a digitized rigid motion result in the existence of 2- and 0-points.

2.2 Neighborhood Motion Map

Let us consider the notion of neighborhood in $\mathbb {Z}^2$.

Definition 2

The neighborhood of $\mathbf {p}\in \mathbb {Z}^2$ (of squared radius $r \in \mathbb {R}_+$ ), denoted $\mathcal {N}_r(\mathbf {p})$, is defined as $\mathcal {N}_r(\mathbf {p}) = \big \{ \mathbf {p}+ \mathbf {d}\in \mathbb {Z}^2 \mid \Vert \mathbf {d}\Vert ^2 \le r \big \}$.

Remark 2

$\mathcal {N}_1$ and $\mathcal {N}_2$ correspond to the 4- and 8-neighborhoods, widely used in digital geometry [4].

In order to track local alterations of a neighborhood during rigid motions, we introduce the notion of a neighborhood motion map.

Definition 3

Given a digitized rigid motion U, the neighborhood motion map of $\mathbf {p}\in \mathbb {Z}^2$ for $r \in \mathbb {R}_+$ is the function $\mathcal {G}^U_r(\mathbf {p}) : \mathcal {N}_r(\mathbf {0}) \rightarrow \mathcal {N}_{r'}(\mathbf {0})$ (with $r' \ge r$) defined as $\mathcal {G}^U_r(\mathbf {p}) : \mathbf {d}\mapsto U(\mathbf {p}+\mathbf {d}) - U(\mathbf {p})$.

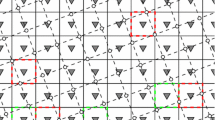
In other words, $\mathcal {G}^U_r(\mathbf {p})$ associates to each relative position of an integer point $\mathbf {p}+ \mathbf {d}$ in the neighborhood of $\mathbf {p}$, the relative position of the image $U(\mathbf {p}+ \mathbf {d})$ in the neighborhood of $U(\mathbf {p})$. The squared radius $r'$ of $\mathcal {N}_{r'}(U(\mathbf {p}))$ is slightly larger than r. For instance, we have $r' = 2$ (resp. 5) for $r = 1$ (resp. 2). Figure 1 presents a visual presentation of $\mathcal {G}^U_r(\mathbf {p})$, where $r = 1, 2$. Note that a similar notion for digitized rotations was previously proposed by Nouvel and Rémila [6].

Fig. 1.

Visual representation of neighborhood motion maps $\mathcal {G}^U_r(\mathbf {p})$ with colors: reference neighborhoods $\mathcal {N}_1(\mathbf {p})$ (a) and $\mathcal {N}_2(\mathbf {p})$ (c), and examples of $\mathcal {G}^U_1(\mathbf {p})$ (b) and $\mathcal {G}^U_2(\mathbf {p})$ (d) (Color figure online).

2.3 Remainder Range Partitioning

Digitized rigid motions $U = \mathcal {D}\ \circ \ \mathcal {U}$ are piecewise constant, which is a consequence of the nature of $\mathcal {D}$. In other words, the neighborhood motion map $\mathcal {G}^U_r(\mathbf {p})$ evolves non-continuously according to the parameters of $\mathcal {U}$ that underlies U. Our purpose is now to express how $\mathcal {G}^U_r(\mathbf {p})$ evolves.

Let us consider an integer point $\mathbf {p}+ \mathbf {d}$ in the neighborhood $\mathcal {N}_r(\mathbf {p})$ of $\mathbf {p}$. From Eq. (1), we have

$$\begin{aligned} \mathcal {U}(\mathbf {p}+ \mathbf {d}) = \mathbf {Rd} + \mathcal {U}(\mathbf {p}). \end{aligned}$$

(3)

We know that $\mathcal {U}(\mathbf {p})$ lies in the unit square centered at the integer point $U(\mathbf {p})$, which implies that there exists a value $\rho (\mathbf {p}) = \mathcal {U}(\mathbf {p}) - U(\mathbf {p}) \in [-\frac{1}{2},\frac{1}{2})^2$. The coordinates of $\rho (\mathbf {p})$, called the remainder of $\mathbf {p}$ under $\mathcal {U}$, are the fractional parts of the coordinates of $\mathcal {U}(\mathbf {p})$; and $\rho$ is called the remainder map under U. As $\rho (\mathbf {p}) \in [-\frac{1}{2},\frac{1}{2})^2$, this range, denoted by $\mathscr {P}= [-\frac{1}{2},\frac{1}{2})^2$, is called the remainder range. Using $\rho$, we can rewrite Eq. (3) by

$$\begin{aligned} \mathcal {U}(\mathbf {p}+ \mathbf {d}) = \mathbf {Rd} + \rho (\mathbf {p}) + U(\mathbf {p}). \end{aligned}$$

Without loss of generality, we can consider that $U(\mathbf {p})$ is the origin of a local coordinate frame of the image space, i.e. $\mathcal {U}(\mathbf {p}) \in \mathscr {P}$. In such local coordinate frame, the former equation rewrites as

$$\begin{aligned} \mathcal {U}(\mathbf {p}+ \mathbf {d}) = \mathbf {Rd} + \rho (\mathbf {p}). \end{aligned}$$

(4)

Still under this assumption, studying the non-continuous evolution of the neighborhood motion map $\mathcal {G}^U_r(\mathbf {p})$ is equivalent to studying the behavior of $U(\mathbf {p}+ \mathbf {d}) = \mathcal {D}\circ \mathcal {U}(\mathbf {p}+ \mathbf {d})$ for $\mathbf {d}\in \mathcal {N}_r(\mathbf {0})$ and $\mathbf {p}\in \mathbb {Z}^2$, with respect to the rotation parameter $\theta$ defining $\mathbf {R}$ and the translation parameters embedded in $\rho (\mathbf {p})$, that deterministically depend on $(t_x,t_y,\theta )$. The discontinuities of $U(\mathbf {p}+ \mathbf {d})$ occur when $\mathcal {U}(\mathbf {p}+ \mathbf {d})$ is on the boundary of a digitization cell. Setting $\rho (\mathbf {p}) = (x,y)^t \in \mathscr {P}$ and $\mathbf {d}= (u,v)^t \in \mathcal {N}_r(\mathbf {0})$, this is formulated by one of the following two formulas

$$\begin{aligned} x + u \cos \theta - v \sin \theta&= k_x + 1/2 \end{aligned}$$

(5)

$$\begin{aligned} y + u \sin \theta + v \cos \theta&= k_y + 1/2 \end{aligned}$$

(6)

where $k_x, k_y \in \mathbb {Z}$. For a given $\mathbf {d}= (u,v)^t$ and $k_x$ (resp. $k_y$), Eq. (5) (resp. (6)) defines a vertical (resp. horizontal) line in the remainder range $\mathscr {P}$, called a vertical (resp. horizontal) critical line. These critical lines with different $\mathbf {d}$, $k_x$ and $k_y$, divide the remainder range $\mathscr {P}$ into rectangular regions called frames. Note that for $r=1$ (resp. $r=2$) there are 4 (resp. 8) vertical and horizontal critical lines, respectively. As long as coordinates of $\rho (\mathbf {p})$ belong to a same frame, the associated neighborhood motion map $\mathcal {G}_r^U(\mathbf {p})$ remains constant.

Proposition 4

For any $\mathbf {p}, \mathbf {q}\in \mathbb {Z}^2$, $\mathcal {G}_r^U(\mathbf {p}) = \mathcal {G}_r^U(\mathbf {q})$ iff $\rho (\mathbf {p})$ and $\rho (\mathbf {q})$ are in the same frame.

A similar proposition was already shown in [6] for the case $r = 1$ and digitized rotations. The above result is then an extension for general cases, such that $r \ge 1$ and digitized rigid motions. An example of the remainder range partitioning is presented in Fig. 2.

Remark 3

Equations (5) and (6) of critical lines are similar to those for digitized rotations, since the translation part is embedded only in $\rho (\mathbf {p}) = (x,y)^t$, as seen in Eq. (4).

2.4 Non-surjective and Non-injective Frames

Some frames correspond to neighborhood motion maps that exhibit 0- or 2-points, implying non-surjectivity or non-injectivity [7].

Lemma 5

$U(\mathbf {p}) + \mathbf {d}_*$ is a 0-point if and only if $\rho (\mathbf {p})$ is in one of the zones $f_*^0$ (union of frames themselves) defined as follows:

$$\begin{aligned}&f_\uparrow ^0 = (1/2-\cos \theta , \sin \theta - 1/2) \times (3/2 -\cos \theta -\sin \theta , 1/2), \\&f_\rightarrow ^0 = (3/2 -\cos \theta -\sin \theta ,1/2) \times (1/2 - \sin \theta , \cos \theta -1/2), \\&f_\downarrow ^0 = (1/2 - \sin \theta , \cos \theta -1/2) \times (-1/2, \cos \theta + \sin \theta -3/2), \\&f_\leftarrow ^0 = (-1/2, \cos \theta + \sin \theta -3/2) \times (1/2 - \cos \theta , \sin \theta - 1/2), \end{aligned}$$

where $*\in \{\uparrow , \rightarrow , \downarrow , \leftarrow \}$ and $\mathbf {d}_\uparrow = (0,1)^t, \mathbf {d}_\rightarrow = (1,0)^t, \mathbf {d}_\downarrow = (0,-1)^t, \mathbf {d}_\leftarrow = (-1,0)^t$.

Lemma 6

$U(\mathbf {p})$ is a 2-point whose preimages are $\mathbf {p}$ and $\mathbf {p}+ \mathbf {d}_*$ if and only if $\rho (\mathbf {p})$ is in one of the zones $f_*^2$ defined as follows:

$$\begin{aligned}&f_\uparrow ^2 = (\sin \theta -1/2, 1/2) \times (-1/2, 1/2-\cos \theta ),\\&f_\rightarrow ^2 = (-1/2, 1/2-\cos \theta ) \times (-1/2, 1/2-\sin \theta ), \\&f_\downarrow ^2 = (-1/2, 1/2-\sin \theta ) \times (\cos \theta -1/2, 1/2),\\&f_\leftarrow ^2 = (\cos \theta -1/2, 1/2) \times (\sin \theta -1/2, 1/2). \end{aligned}$$

We can characterize the non-surjectivity and non-injectivity of a digitized rigid motion by the presence of $\rho (\mathbf {p})$ in these specific zones. Both types of the zones are presented in Fig. 2.

Fig. 2.

Examples of remainder range partitioning for: $r=1$ (a), and $r=2$ (b). Non-injective zones $f_*^2$ and non-surjective zones $f_*^0$ are illustrated by red and brown rectangles, respectively (Color figure online).

3 Globally Bijective Digitized Rigid Motions

A digitized rigid motion is bijective if and only if there is no $\rho (\mathbf {p})$, for all $\mathbf {p}\in \mathbb {Z}^2$, in non-surjective and non-injective zones of $\mathscr {P}$. In this section, we characterize bijective rigid motions on $\mathbb {Z}^2$ while investigating such local conditions.

Let us start with the rotational part of the motion. We know from [7] that rotations with any angle of irrational sine or cosine are non-bijective; indeed such rotations have a dense image by $\rho$ (there exists $\mathbf {p}\in \mathbb {Z}^2$ such that $\rho (\mathbf {p})$ lies in a non-surjective or/and non-injective zone of $\mathscr {P}$). This result is also applied to U, whatever translation part is added.

Therefore, we focus on rigid motions for which both cosine and sine of the angle $\theta$ are rational. Such angles are called Pythagorean angles [7] and are defined by primitive Pythagorean triples $(a,b,c) = (p^2 - q^2, 2pq, p^2 + q^2)$ with $p,q \in \mathbb {Z}, p > q$ and $p - q$ is odd, such that (a, b, c) are pairwise coprime, and cosine and sine of such angles are $\frac{a}{c}$ and $\frac{b}{c}$, respectively. The image of $\mathbb {Z}^2$ by $\rho$ when U is a digitized rational rotation corresponds to a cyclic group $\mathscr {G}$ on the remainder range $\mathscr {P}$, which is generated by $\pmb {\psi }= \left( \frac{p}{c}, \frac{q}{c} \right) ^t$ and $\pmb {\omega }= ( -\frac{q}{c}, \frac{p}{c})^t$ and whose order is equal to $c = p^2 + q^2$ [7]. When U contains a translation part, the image of $\rho$ in $\mathscr {P}$, which we will denote by $\mathscr {G}'$, is obtained by translating $\mathscr {G}$ (modulo $\mathbb {Z}^2$) and $|\mathscr {G}'|$ is equal to the order of $\mathscr {G}$, its underlying group. Note also that a digitized rational rotation is bijective (the intersection of $\mathscr {G}$ with non-injective and non-surjective regions is empty) iff its angle comes from a twin Pythagorean triple—a primitive Pythagorean triple with the additional condition $p = q + 1$—see Nouvel and Rémila [7] and, more recently, Roussillon and Cœurjolly [9].

Our question is then whether a digitized rigid motion can be bijective, even when the corresponding rotation is not. In order to answer this question, we use the following equivalence property: digitized rational rotations are bijective if they are surjective or injective [7]. Indeed, this allows us to focus only on non-surjective zones.

Proposition 7

A digitized rigid motion whose rotational part is given by a non-twin Pythagorean primitive triple is always non-surjective.

Proof

We show that no translation factor can prevent the existence of an element of $\mathscr {G}'$ in a non-surjective zone. We consider the length of a side of $f_*^0$, given by $L_1=\frac{2q(p-q)}{c}$, and the side of the bounding box of a fundamental square in $\mathscr {G}$, given by $L_2 = \frac{p+q}{c}$. Note that any non-surjective zone $f_*^0$ also forms a square. As $p>q+1$, $L_2 < L_1$, and thus $\mathscr {G}' \cap f_*^0 \ne \varnothing$ (see Fig. 3(a)).        $\square$

If, on the contrary, the rotational part is given by a twin Pythagorean triple, i.e. is bijective, the rigid motion is also bijective, under the following condition.

Proposition 8

A digitized rigid motion is bijective if and only if it is composed of a rotation by an angle defined by a twin Pythagorean triple and a translation $\mathbf {t}= \mathbf {t}' + \mathbb {Z}\pmb {\psi }+ \mathbb {Z}\pmb {\omega }$, where $\mathbf {t}' \in \left( -\frac{1}{2c}, \frac{1}{2c}\right) ^2$.

Proof

Let us first consider the case $\mathbf {t}= \mathbf {0}$. Since $L_2>L_1$, there exists a fundamental square in $\mathscr {G}$, i.e. whose vertices are $(n \pmb {\omega }+m \pmb {\psi }),((n+1) \pmb {\omega }+m \pmb {\psi }), ((n+1) \pmb {\omega }+(m+1) \pmb {\psi }), (n \pmb {\psi }+(m+1) \pmb {\psi })$, where $n,m \in \mathbb {Z}$, and the vertices lie outside of $f_\downarrow ^0$, at $N_\infty$ distance 1/2c (see Fig. 3(b)). Now let us consider the case $\mathbf {t}\ne \mathbf {0}$. The above four vertices are the elements of $\mathscr {G}$ closest to $f_\downarrow ^0$, therefore if $N_\infty (\{\mathbf {t}\}) < 1/2c$, where $\{.\}$ stands for the fractional part function, then $\mathscr {G}' \cap f_\downarrow ^0 = \varnothing$. Moreover, if $N_\infty (\{\mathbf {t}\})$ is slightly above 1/2c, then it is plain that some point of $\mathscr {G}'$ will enter the frame $f_\downarrow ^0$. But $\mathscr {G}$ is periodic with periods $\pmb {\omega }$ and $\pmb {\psi }$, so that the set of admissible vectors $\mathbf {t}$ has the same periods. Then we see that the admissible vectors form a square (i.e. a $N_\infty$ ball of radius 1/2c) modulo $\mathbb {Z}\pmb {\psi }+ \mathbb {Z}\pmb {\omega }$ (see Fig. 3(c)).        $\square$

Fig. 3.

Examples of remainder range partitioning together with $\mathscr {G}$ obtained for rotations by Pythagorean angles. (a) The non-bijective digitized rotation defined by the primitive Pythagorean triple (12, 35, 37) and (b) the bijective digitized rotation defined by the twin Pythagorean triple (7, 24, 25). The non-surjective and non-injective zones are illustrated by brown and red rectangles, respectively. (c) A fundamental square in $\mathscr {G}$ whose vertices are $(n \pmb {\omega }+m \pmb {\psi }),((n+1) \pmb {\omega }+m \pmb {\psi }), ((n+1) \pmb {\omega }+(m+1) \pmb {\psi }), (n \pmb {\psi }+(m+1) \pmb {\psi })$, represented by black circles, and $f_\downarrow ^0$ in brown. The union of the areas filled with a line pattern form a square (i.e. a $N_\infty$ ball of radius $\frac{1}{2c}$) of the admissible translation vectors modulo $\mathbb {Z}\pmb {\psi }+ \mathbb {Z}\pmb {\omega }$ (Color figure online).

4 Locally Bijective Digitized Rigid Motions

As seen above, the bijective digitized rigid motions, though numerous, are not dense in the set of all digitized rigid motions. We may thus generally expect defects such as 2-points. However, in practical applications, the bijectivity of a given U on the whole $\mathbb {Z}^2$ is not the main issue; rather, one usually works on a finite subset of the plane (e.g., a rectangular digital image). The relevant question is then: “given a finite subset $S \subset \mathbb {Z}^2$, is U restricted to S bijective?”. Actually, the notion of bijectivity in this question can be replaced by the notion of injectivity since the surjectivity is trivial, due to the definition of U that maps S to U(S).

The basic idea for such local bijectivity verification is quite natural. Because of its quasi-isometric property, a digitized rigid motion U can send at most two 4-neighbors to a same point (Remark 1). Thus, the lack of injectivity is a purely local matter, suitably handled by the neighborhood motion maps via the remainder map. Indeed, in accordance with Lemma 6, U is non-injective, with respect to S iff there exists $\mathbf {p}\in S$ such that $\rho (\mathbf {p})$ lies in the union $\mathcal {F}= f_\downarrow ^2 \cup f_\uparrow ^2 \cup f_\leftarrow ^2 \cup f_\rightarrow ^2$ of all non-injective zones. We propose two algorithms making use of the remainder map information, as an alternative to a brute force verification.

The first—forward—algorithm, verifies for each point $\mathbf {p}\in S$ the inclusion of $\rho (\mathbf {p})$ in one of the non-injective regions of $\mathcal {F}$. The second—backward—algorithm first finds all points $\mathbf {w}$ in $\mathscr {G}' \cap \mathcal {F}$, called the non-injective remainder set, and then verifies if their preimages $\rho ^{-1}(\mathbf {w})$ are in S.

Both algorithms apply to rational motions, i.e., with a Pythagorean angle given by a primitive Pythagorean triple $(a,b,c) = (p^2 - q^2, 2 p q, p^2 + q^2)$ and a rational translation vector $\mathbf {t}= (t_x,t_y)^t$. We capture essentially the behavior for all angles and translation vectors, since rational motions are dense. Methods for angle approximation by Pythagorean triples up to a given precision may be found in [1]. These assumptions guarantee the exact computations of the algorithms, which are based on integer numbers.

4.1 Forward Algorithm

The strategy consists of checking whether the remainder map $\rho (\mathbf {p})$ of each $\mathbf {p}\in S$ belongs to one of non-injective zones $f^2_*$ defined in Lemma 6; if this is the case, we check additionally whether $\mathbf {p}+ \mathbf {d}_* \in \mathcal {N}_1(\mathbf {p})$ belongs to S; otherwise, there is no 2-point with $\mathbf {p}$ under $U_{\mid S}$.

This leads to the forward algorithm, which returns the set B of all pairs of points having the same image. We can then conclude that $U_{|S}$ is bijective iff $B = \varnothing$; in other words, U is injective on $S \backslash B$. The break statement on line comes from the fact that there is no 3-point. Also from Remark 1, we restrict the internal loop to the set $\{\rightarrow ,\downarrow \}$.

The main advantage of the forward algorithm lies in its simplicity. In particular, we can directly check which neighbor $\mathbf {p}+ \mathbf {d}_*$ of $\mathbf {p}$ constitutes a 2-point with $\mathbf {p}$. Because rational rigid motions are exactly represented by integers, it can be verified without numerical error and in a constant time if $\rho (\mathbf {p}) \in \mathcal {F}$. The time complexity of this algorithm is $\mathscr {O}(|S|)$. Figure 4 illustrates the forward algorithm.

Remark 4

The forward algorithm can be used with non-rational rotations, at the cost of a numerical error.

Fig. 4.

(a) An initial finite set $S \subset \mathbb {Z}^2$, colored in black. (b) The remainder map image of S, i.e. $\rho (\mathbf {p})$ for all $\mathbf {p}\in S$, under U— given by parameters $\left( \arccos \frac{6}{37}, 0, \frac{2}{25}\right)$. Since no point $\rho (\mathbf {p})$ lies within the non-injective zone $\mathcal {F}$, we have a visual proof that U restricted to S is injective (Color figure online).

4.2 Backward Algorithm

In this section, we consider a rectangular finite set S as the input; this setting is not abnormal as we can find a bounding box for any finite set. The strategy of the proposed backward algorithm consists of: Step 1: for a given U, i.e. a Pythagorean triple and a rational translation vector, listing all the points $\mathbf {w}$ in the non-injective remainder set; Step 2: finding all their preimages $\rho ^{-1}(\mathbf {w})$; Step 3: finding among them those in S.

Step 1. As explained in Sect. 3, the cyclic group $\mathscr {G}$ is generated by $\pmb {\psi }= \left( \frac{p}{c}, \frac{q}{c} \right) ^t$ and $\pmb {\omega }= \left( -\frac{q}{c}, \frac{p}{c} \right) ^t$, and $\mathscr {G}'$ is its translation (modulo $\mathbb {Z}^2$). Therefore, all the points in $\mathscr {G}'$ can be expressed as $\mathbb {Z}\pmb {\psi }+ \mathbb {Z}\pmb {\omega }+ \{\mathbf {t}\}$. To find these points of $\mathscr {G}'$ in the non-injective zones, let us focus on $f_\downarrow ^2$ given in Lemma 6. Note that the similar discussion is valid for other non-injective zones given by Lemma 6. The set of remainder points $\mathbb {Z}\pmb {\psi }+ \mathbb {Z}\pmb {\omega }+ \{\mathbf {t}\}$ lying in $f_\downarrow ^2$ is then formulated by the following four linear inequalities, and we define the non-injective remainder index set $C_\downarrow$ such that

(7)

Solving the system of inequalities in (7) consists of finding all pairs $(i,j) \in \mathbb {Z}^2$ inside the given rectangle. This is carried out by mapping $\mathbb {Z}\pmb {\psi }+ \mathbb {Z}\pmb {\omega }+ \{\mathbf {t}\}$ to $\mathbb {Z}^2$ using a similarity; denoting by $\hat{f}_\downarrow ^2$ the image of $f_\downarrow ^2$ under this transformation (Fig. 5).

To list all the integer points in $(i,j) \in C_\downarrow$, we first find the upper and lower corners of the rectangular region $\hat{f}_\downarrow ^2$ given by Eq. (7): $(\frac{p - 3 q}{2}, \frac{p - q}{2})$ and $( \frac{q - p}{2}, \frac{p + q}{2})$. We then find all the horizontal lines $j=k$ where $k \in \mathbb {Z}\cap ( \frac{p - q}{2}, \frac{p + q}{2})$. For each line $j=k$, we obtain the two intersections with the boundary of $\hat{f}_\downarrow ^2$ as the maximal and minimal integers for i.

The complexity of this step depends on the number of integer lines crossing $\hat{f}_\downarrow ^2$, which is q, and thus it is $\mathscr {O}(q)$. This completes Step 1.

Fig. 5.

(a) Geometrical interpretation of the system of linear inequalities in Eq. (7), in the (i, j)-plane for $(p,q)=(7,2)$. The region surrounded by the four lines is $\hat{f}_\downarrow ^2$, and the integer points within are marked by black circles. (b) The remainder range, $\mathscr {G}'$ and $f_\downarrow ^2$ illustrated by a red square, which corresponds to $\hat{f}_\downarrow ^2$ in (a) (Color figure online).

Step 2. We seek for the set of all preimages of $i \pmb {\psi }+ j \pmb {\omega }+ \{\mathbf {t}\}$ for each $(i,j) \in C_\downarrow$, or equivalently, preimages of $i \pmb {\psi }+ j \pmb {\omega }$ by the translationless remainder map. (The fact that this point is in $f_\downarrow ^2$ plays no role in this step.) This is a Diophantine system (modulo $\mathbb {Z}^2$) and the set of preimages of a point $i \pmb {\psi }+ j \pmb {\omega }+ \{\mathbf {t}\}$ is given by a sublattice of $\mathbb {Z}^2$:

$$\begin{aligned} \mathbb {T}(i,j) = p \frac{\mu - v}{2} \begin{pmatrix}i \\ j \end{pmatrix} + \mathbb {Z}\begin{pmatrix} a \\ -b \end{pmatrix} + \mathbb {Z}\begin{pmatrix} c \sigma \\ c \tau \end{pmatrix} \end{aligned}$$

(8)

where $\mu , v$ and $\sigma , \tau$ are the Bézout coefficients satisfying $\mu p^2 + v q^2 = 1$ and $\sigma a + \tau b =1$, respectively.

Fig. 6.

Non-injective pixels obtained for a computer tomography image of a human chest by the backward algorithm (preimages of points in $\mathscr {G}' \cap f_\downarrow ^2$). Each non-injective pixel is marked by a circle. Pixels of the same color are positioned periodically and are preimages of the same point in $\mathscr {G}' \cap f_\downarrow ^2$. The result was obtained for $\theta = \arcsin \frac{591}{19409} \approx 1.7^\circ$ and $\mathbf {t}=\mathbf {0}$. Note that from the point of view of backward algorithm the content of the image does not matter (Color figure online).

To find these Bézout coefficients, we use the extended Euclidean Algorithm. The time complexity of finding $\mu$ and v (resp. $\sigma$ and $\tau$) is $\mathscr {O}(\log {q})$ (resp. $\mathscr {O}(\log {\min (a,b)})$ [2]. As the Bézout coefficients are computed once for all $(i,j) \in C_\downarrow$, the time complexity of Step 2 is $\mathscr {O}(\log {q}) + \mathscr {O}(\log {\min (a,b)}) = \mathscr {O}(\log {\min (a,b)})$.

Step 3. We now consider the union of lattices $\mathbb {T}(i,j)$ for all couples (i, j) in $C_\downarrow$ obtained in Step 1. To find their intersection with S, we apply to each an algorithm similar to Step 1, with an affine transformation mapping the basis $({\begin{matrix} a \\ -b \end{matrix}}), ({\begin{matrix} c \sigma \\ c \tau \end{matrix}})$ to $({\begin{matrix} 1 \\ 0 \end{matrix}}) , ({\begin{matrix} 0 \\ 1 \end{matrix}})$ and $p \frac{\mu - v}{2} ({\begin{matrix} i \\ j \end{matrix}})$ to $({\begin{matrix} 0 \\ 0 \end{matrix}})$. Thus, a rectangular S maps to a quadrangular $\hat{S}$ after such an affine transformation, and we find the set of integer points in $\hat{S}$. Note that the involved transformation is the same for all the lattices, up to a translation.

The complexity of listing all the preimages is given by $|C_\downarrow |$ times the number of horizontal lines $j = k, k\in \mathbb {Z}$, passing $\hat{S}$, denoted by K. The cardinality of $C_\downarrow$ is related to the area of $f_\downarrow ^2$ given by $\frac{2 q^2 (p - q)^2}{(p^2 + q^2)^2}$ which cannot be larger than $\frac{3}{2} - \sqrt{2}$. As $|\mathscr {G}'| = c$ and $|C_\downarrow | = |\mathscr {G}' \cap f_\downarrow ^2|, |C_\downarrow | \le (\frac{3}{2} - \sqrt{2}) c$. On the other hand, K is bounded by $d_S/c$, where $d_S$ stands for the diagonal of S. As the complexity of $d_S$ is given by $\mathscr {O}(\sqrt{|S|})$, the final complexity of Step 3 is $\mathscr {O}(\sqrt{|S|})$.

Remark 5

A possible refinement consists of ruling out false positives at border points $\mathbf {p}$ of S, by checking whether $\mathbf {p}+ \mathbf {d}_*$ belongs to S, where $\mathbf {d}_*$ is given by the above procedure (thus avoiding the case when $\mathbf {p}$ and $\mathbf {p}+\mathbf {d}_*$ are mapped to the same point but $\mathbf {p}+\mathbf {d}_*$ is not in S). This can be achieved during Step 3.

All the steps together allow us to state that the backward algorithm, whose time complexity is $\mathscr {O}(q + \log \min (a,b) + \sqrt{|S|})$, identifies non-injective points in finite rectangular sets. Figure 6 presents an experimental result of the backward algorithm applied to a computer tomography image.

Remark 6

Even though the backward algorithm works with rectangles, one can approximate any set S by a union of rectangles and run the backward algorithm on each of them.

5 Conclusion

In this article, we have extended the neighborhood motion maps—which was previously proposed by Nouvel and Rémila [7] for digitized rotations—and we have shown that they are useful to characterize the bijectivity of rigid motions on $\mathbb {Z}^2$.

We first proved some necessary and sufficient conditions of bijective rigid motions on $\mathbb {Z}^2$; i.e., rigid motions such that no point $\mathbf {p}\in \mathbb {Z}^2$ has the image $\rho (\mathbf {p})$ in either non-injective zones or non-surjective zones. Then, from a more practical point of view, we focused on finite sets of $\mathbb {Z}^2$ rather than the whole $\mathbb {Z}^2$. In particular, we proposed two efficient algorithms for verifying whether a given digitized rigid motion is bijective when restricted to a finite set S. The forward algorithm consists of checking if points of S have preimages in non-injective zones. On the other hand, we used the reverse strategy to propose the backward algorithm consisting of the identification of points in $\mathscr {G}' \cap \mathcal {F}$ and their preimages in S. The complexities of the forward and backward algorithms are $\mathscr {O}{(|S|)}$ and $\mathscr {O}(q + \log \min (a,b) + \sqrt{|S|})$, respectively.

One of our perspectives is to extend the proposed framework to 3D digitized rigid motions.