iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://link.springer.com/10.1007/s00454-016-9762-x?fromPaywallRec=false
On the Diameter of Lattice Polytopes | Discrete & Computational Geometry Skip to main content
Springer Nature Link
Log in

On the Diameter of Lattice Polytopes

  • Published:
Discrete & Computational Geometry Aims and scope Submit manuscript

Abstract

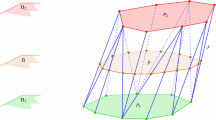
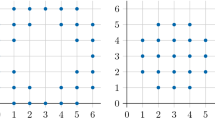
In this paper we show that the diameter of a d-dimensional lattice polytope in \([0,k]^n\) is at most \({\lfloor }{\left( k-\frac{1}{2}\right) d}{\rfloor }\). This result implies that the diameter of a d-dimensional half-integral polytope is at most \({\lfloor }{\frac{3}{2} d}{\rfloor }\). We also show that for half-integral polytopes the latter bound is tight for any d.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Abeledo, H.G., Rothblum, U.G.: Stable matchings and linear inequalities. Discrete Appl. Math. 54, 1–27 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  2. Balinski, M.L.: Integer programming: methods, uses, computation. Manage. Sci. Ser. A 12, 253–313 (1965)

    MathSciNet  MATH  Google Scholar 

  3. Balog, A., Bárány, I.: On the convex hull of the integer points in a disc. In: Proceedings of the Seventh Annual Symposium on Computational Geometry, SCG ’91, pp. 162–165. ACM, New York, NY, USA (1991)

  4. Bonifas, N., Di Summa, M., Eisenbrand, F., Hähnle, N., Niemeier, M.: On sub-determinants and the diameter of polyhedra. Discrete Comput. Geom. 52(1), 102–115 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  5. Brønsted, A.: An Introduction to Convex Polytopes. Springer, Berlin (1983)

    Book  Google Scholar 

  6. Chena, X., Ding, G., Hu, X., Zang, W.: The maximum-weight stable matching problem: duality and efficiency. SIAM J. Discrete Math. 26(3), 1346–1360 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Deza, M.M., Laurent, M.: Geometry of Cuts and Metrics. Algorithms and Combinatorics. Springer, Berlin (1997)

    Book  MATH  Google Scholar 

  8. Gijswijt, D., Pap, G.: An algorithm for weighted fractional matroid matching. J. Comb. Theory Ser. B 103, 509–520 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kleinschmidt, P., Onn, S.: On the diameter of convex polytopes. Discrete Math. 102, 75–77 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  10. Naddef, D.J.: The Hirsch conjecture is true for \((0,1)\)-polytopes. Math. Program. 45, 109–110 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  11. Naddef, D.J., Pulleyblank, W.R.: Hamiltonicity in \((0,1)\)-polyhedra. J. Comb. Theory Ser. B 37(1), 41–52 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  12. Padberg, M.: The boolean quadric polytope: some characteristics, facets and relatives. Math. Program. 45, 139–172 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  13. Schrijver, A.: Theory of Linear and Integer Programming. Wiley, Chichester (1986)

    MATH  Google Scholar 

  14. Schrijver, A.: Combinatorial Optimization. Polyhedra and Efficiency. Springer, Berlin (2003)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial and Systems Engineering & Wisconsin Institute for Discovery, University of Wisconsin-Madison, Madison, WI, USA

    Alberto Del Pia

  2. Wisconsin Institute for Discovery, University of Wisconsin-Madison, Madison, WI, USA

    Carla Michini

Authors
  1. Alberto Del Pia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Carla Michini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Carla Michini.

Additional information

Editor in Charge: Günter M. Ziegler

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Del Pia, A., Michini, C. On the Diameter of Lattice Polytopes. Discrete Comput Geom 55, 681–687 (2016). https://doi.org/10.1007/s00454-016-9762-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00454-016-9762-x

Keywords

Search

Navigation