Utente:WATCHDOG/Circuito RC

Intestazione

Stubby

Questa voce è solo un abbozzo. Se puoi, contribuisci adesso a migliorarla secondo le convenzioni di Wikipedia.
Per l'elenco completo degli abbozzi, vedi la relativa categoria. Se appropriato, utilizza uno degli altri template abbozzi più specifici

UNDER CONSTRUCTION

Un circuito RC è una delle configurazioni di filtro elettronico più semplici. E' composto da una resistenza R e da una capacità C poste in serie, oppure in parallelo, alimentate da un generatore elettrico (salvo diversamente indicato considereremo generatori di tensione).

A seconda di come sono disposti i due componenti il circuito RC può filtrare le frequenze basse (filtro passa-basso) oppure quelle alte (filtro passa-alto), realizzando un filtro di primo ordine.

Per le sue caratteristiche questo circuito è basilare per funzioni quali la pulizia di un segnale e nei sintetizzatori.

Sfruttando il principio di carica e scarica del condensatore, questa configurazione trova utilizzo anche come oscillatore. In particolare, soprattutto nella didattica, è utilizzato per la generazione di segnali di clock (vedere abbinamento con Trigger di Schmitt per creare segnali di tipo logici). Tuttavia, vista la variabilità dei comportamenti del condensatore in funzione delle condizioni ambientali, questa configurazione è utilizzata nelle applicazioni in cui la temporizzazione non necessita grande precisione.

Introduzione

Esistono tre componenti circuitali passivi di base nell'elettronica analogica: la resistenza R, il condensatore C, l'induttanza L. Questi elementi posso essere combinati in quattro configurazioni circuitali di base: il circuito RC, il circuito RL, il circuito LC e il circuito RLC (le abbreviazioni indicano quali componenti di base vengono usati). Questi circuiti manifestano dei comportamenti che sono di fondamentale importanza nell'elettronica analogica. In particolare, questi circuiti possono comportarsi come filtri elettronici passivi. Nota, in questo articolo faremo riferimento al concetto più generale di capacità piuttosto che di condensatore.

Questo articolo necessita da parte del lettore la conoscenza della rappresentazione dell'impedenza complessa e la conoscenza della rappresentazione dei segnali nel dominio della frequenza.

Impedenza complessa

L'impedenza complessa Z_C (in ohms) di un condensatore di capacità C (in farads) è: $Z_{C}={\frac {1}{sC}}$

La frequenza complessa s è, generalmente, un numero complesso

$s\ =\ \sigma +j\omega$

avendo indicato con,

• j rappresenta l'unità immaginaria:

$j={\sqrt {-1}}$

• $\sigma \$ è il coefficiente di smorzamento esponenziale (in radianti al secondo), e

• $\omega \$ è la frequenza angolare sinusoidale (in radianti al secondo).

Ingresso sinusoidale

Nel caso particolare in cui l'ingresso consista di un segnale sinusoidale puro (senza smorzamento esponenziale) si ha:

$\sigma \ =\ 0$

e la variabile complessa s (nel dominio di Laplace) viene sostituita dalla frequenza complessa:

$s\ =\ j\omega$

Circuito RC in serie

Circuito RC serie

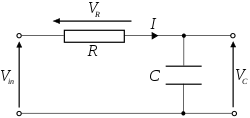
Applicando la regola del partitore di tensione al circuito di figura la tensione ai capi della capacità è data da:

$V_{C}(s)={\frac {1/Cs}{R+1/Cs}}V_{in}(s)={\frac {1}{1+RCs}}V_{in}(s)$

mentre la tensione ai capi della resistenza è:

$V_{R}(s)={\frac {R}{R+1/Cs}}V_{in}(s)={\frac {RCs}{1+RCs}}V_{in}(s)$.

Funzione di trasferimento

La funzione di trasferimento per la capacità

$H_{C}(s)={V_{C}(s) \over V_{in}(s)}={1 \over 1+RCs}=G_{C}e^{j\phi _{C}}$ .

Analogamente la funzione di trasferimento per la resistenza è data da:

$H_{R}(s)={V_{R}(s) \over V_{in}(s)}={RCs \over 1+RCs}=G_{R}e^{j\phi _{R}}$ .

Poli e zeri

Entrambe le funzioni di trasferimento sono a polo singolo situato in:

$s=-{1 \over RC}$ .

La funzione di trasferimento della resistenza, inoltre, ha anche un zero all'origine.

Guadagno e fase

Il guadagno dei due componenti è dato da:

$G_{C}=|H_{C}(s)|=\left|{\frac {V_{C}(s)}{V_{in}(s)}}\right|={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}$

e

$G_{R}=|H_{R}(s)|=\left|{\frac {V_{R}(s)}{V_{in}(s)}}\right|={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}$,

mentre le fasi sono:

$\phi _{C}=\angle H_{C}(s)=\tan ^{-1}\left(-\omega RC\right)$

e

$\phi _{R}=\angle H_{R}(s)=\tan ^{-1}\left({\frac {1}{\omega RC}}\right)$.

Sostituendo queste espressioni nell'usuale rappresentazione a fasori nelle tensioni della resistenza e del capacità si ottiene:

$V_{C}\ =\ G_{C}V_{in}e^{j\phi _{C}}$

$V_{R}\ =\ G_{R}V_{in}e^{j\phi _{R}}$.

Corrente

La corrente è data da:

$I(s)={\frac {V_{in}(s)}{R+1/Cs}}={Cs \over 1+RCs}V_{in}(s)$

Si noti che la corrente che scorre nella resistenza e quella che scorre nel condensatore hanno lo stesso valore, essendo connessi in seie.

Risposta impulsiva

La risposta impulsiva per ogni tensione è data dall'inverso della trasformata di Laplace della corrispondente funzione di trasferimento. Tale risposta rappresenta la risposta del circuito ad un ingresso impulsivo (comunemente noto in matematica come funzione delta o impulso di Dirac).

La risposta impulsiva della tensione del condensatore è:

$h_{C}(t)={1 \over RC}e^{-t/RC}u(t)={1 \over \tau }e^{-t/\tau }u(t)$

dove u(t) è la funzione a gradino Heaviside step function e

$\tau \ =\ RC$

è la costante di tempo.

Analogamente, la risposta impulsiva della tensione della resistenza è:

$h_{R}(t)=\delta (t)-{1 \over RC}e^{-t/RC}u(t)=\delta (t)-{1 \over \tau }e^{-t/\tau }u(t)$

dove d(t) è la funzione impulso impulso di Dirac.

Dominio della frequenza

Le espressioni sopra riportate sono date nel dominio della frequenza e quindi forniscono il comportamento del circuito nei confronti delle frequenze che costituiscono il segnale d'ingresso. Considerando i casi limita di frequenza che tende all'infinito e frequenza che tende a zero (continua) possiamo notare che:

Per $\omega \to \infty$:

$G_{C}\to 0$

$G_{R}\to 1$.

Per $\omega \to 0$:

$G_{C}\to 1$

$G_{R}\to 0$.

Questo mostra come se l'uscita è presa ai capi della capacità, le alte frequenze vengono attenuate (reiette) e le basse frequenze non vengono attenuate e passano. Perciò il circuito si comporta come un filtro passa basso. Se invece l'uscita è presa ai capi della resistenza le alte frequenze passano mentre le basse vengono attenuate (reiette). In questa configurazione il circuito si comporta come un filtro passa alto.

La gamma di frequenze che passano attraverso il filtro è chiamato banda passante. Il punto in cui il filtro attenua il segnale in modo che abbia metà potenza rispetto al segnale d'ingresso è riferito come frequenza di taglio.

Risolvendo le equazioni di cui sopra otteniamo:

$\omega _{c}={\frac {1}{RC}}$rad/s

o

$f_{c}={\frac {1}{2\pi RC}}$Hz

Che è la frequenza di taglio a metà potenza. Nelle applicazioni tecniche questa frequenza di taglio viene anche chiamata anche "a meno 3dB" poichè il segnale d'ingresso risulta attenuato (in ampiezza) di 3 decibel rispetto all'ingresso.

Ovviamente, anche la fase dipende dalla frequenza:

Per $\omega \to 0$:

$\phi _{C}\to 0$

$\phi _{R}\to 90^{\circ }=\pi /2^{c}$.

Per $\omega \to \infty$:

$\phi _{C}\to -90^{\circ }=-\pi /2^{c}$

$\phi _{R}\to 0$

Perciò in condizioni di corrente continua (0 Hz), la tensione della capacità è in fase con la tensione d'ingresso mentre la tensione della resistenza è in anticipo di 90° rispetto all'ingresso. All'aumentare della frequenza la tensione della capacità tende a ritardare di 90° e la tensione della resistenza tende ad essere in fase rispetto al segnale d'ingresso.

Dominio del tempo

Questa sezione richiede la conoscenza del concetto di e (costante di Nepero). e dei concetti di integrazione e derivazione (vedi Analisi Matematica).

Il modo più diretto per ottenere il comportamento nel dominio del tempo è di usare la Trasformata di Laplace delle tensioni $V_{C}$ e $V_{R}$ ottenute sopra.

In pratica si effettua il seguente cambio di variabile: $j\omega \to s$. Assumendo un ingresso a gradino (esempio: $V_{in}=0$ prima di $t=0$ e $V_{in}=V$ successivamente):

$V_{in}(s)=V{\frac {1}{s}}$

$V_{C}(s)=V{\frac {1}{1+sRC}}{\frac {1}{s}}$

e

$V_{R}(s)=V{\frac {sRC}{1+sRC}}{\frac {1}{s}}$.

Capacitor voltage step-response.

Resistor voltage step-response.

Sviluppando le espressioni e applicando la trasformata inversa di Laplace si ottiene:

$\,\!V_{C}(t)=V\left(1-e^{-t/RC}\right)$

$\,\!V_{R}(t)=Ve^{-t/RC}$.

Perciò la tensione ai capi della capacità tende esponenzialmente ad assumere il valore della tensione d'ingresso V mentre la tensione ai capi della resistenza tende esponenzialmente a zero, al tendere del tempo all'infinito, come mostrato in figura.

Queste equazioni mostrano che un circuito RC in serie ha una costante di tempo, generalmente indicata $\tau =RC$ definita come il tempo che impiega la tensione del componente considerato ad aumentare (su C) o diminuire (su R) di un valore pari a 1/e del valore finale. In altre parole, $\tau$ è il tempo che impega $V_{C}$ per raggiungere $V(1-1/e)$ e $V_{R}$ per raggiungere $V(1/e)$.

Il tasso di variazione]] è: $\left(1-{\frac {1}{e}}\right)$ per $\tau$. Quindi, andando dal tempo $t=N\tau$ a $t=(N+1)\tau$,la tensione cambierà di circa il 63% rispetto al valore iniziale all'istante $t=N\tau$. Pertanto la capacità C si sarà carica al 63% circa dopo un tempo pari a $\tau$, e praticamente completamente carica (99.3%) dopo un tempo di circa $5\tau$. Rimpiazzando il generatore d'ingresso con un cortocircuito, in condizioni di capacità C completamente carica, la tensione $V_{C}$ diminuirà esponenzialmente dal valore V a 0 allo scorrere del tempo. C si sarà scaricata al 37% circa dopo un tempo pari a $\tau$, e praticamente perderà completamente la sua carica (0.7%) dopo un tempo pari a$5\tau$. Si noti che la corrente ha un comportamento simile alla tensione ai capi di R tramite la legge di Ohm.

Questi risultati possono essere ottenuti anche risolvendo le equazioni differenziali che governano il circuito:

${\frac {V_{in}-V_{C}}{R}}=C{\frac {dV_{C}}{dt}}$

e

$\,\!V_{R}=V_{in}-V_{C}$.

Integratore

Considerando l'uscita ai capi la capacitàalle alte frequenze, ad esempio

$\omega >>{\frac {1}{RC}}$.

Questo significa che la tensione ai capi della capicità è molto piccola in quanto la capacità non ha sufficiente tempo per caricarsi. Perciò la tensione ai capi della resistenza è approssimativamente pari alla tensione d'ingresso. Per vedere questo aspetto consideriamo l'espressione per la corrente $I$ data in basso:

$I={\frac {V_{in}}{R+1/j\omega C}}$

Imponendo la condizione della pulsazione sopra riportata si nota che il secondo addendo al denominatore è trascurabile rispetto a R e quindi:

$\omega C>>{\frac {1}{R}}$

perciò

$I\approx {\frac {V_{in}}{R}}$ che è in pratica la legge di Ohm.

Ora, essendo

$V_{C}={\frac {1}{C}}\int _{0}^{t}Idt$

Sostituendo il valore della corrente otteniamo:

$V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{in}dt$,

che è l'equazione di un integrator ai capi del condensatore.

Derivatore

Considerando l'uscita ai capi della resistenza alle basse frequenze, esempio:

$\omega <<{\frac {1}{RC}}$.

Questo significa che la capacità ha tempo sufficiente a caricarsi fino ad un valore approssimativamente pari a quella del segnale d'ingresso. Considerando ancora l'espressione per $I$, essendo:

$R<<{\frac {1}{\omega C}}$,

si ha:

$I\approx {\frac {V_{in}}{1/j\omega C}}$

$V_{in}\approx {\frac {I}{j\omega C}}\approx V_{C}$

Pertanto,

$V_{R}=IR=C{\frac {dV_{C}}{dt}}R$

$V_{R}\approx RC{\frac {dV_{in}}{dt}}$

che è l'equazione di un derivatore ai capi della resistenza.

Nelle applicazioni pratiche, quando si necessita di maggiore accuratezza per le operazioni di integrazione d derivazione, si usano apposite reti di resistori e condensatori all'ingresso e nell'anello di retroazione di un amplificatore operazionale.

Circuito RC parallelo

Parallel RC circuit

Il circuito RC in parallelo è generalmente di interesse inferiore rispetto alla configurazione in serie. Ciò è dovuto al fatto che la tensione d'uscita è pari a quella d'ingresso e quindi non viene effettuata alcuna operazione di filtraggio. Diverso il discorso se si utilizza un generatore di corrente. In questo caso otteniamo usando le impedenze complesse:

$I_{R}={\frac {V_{in}}{R}}\,$

e

$I_{C}=j\omega CV_{in}\,$.

Questo mostra che la corrente della capacità è sfasata di 90° rispetto alla corrente nella resistenza e del generatore.

In alternativa si possono usare l'equivalenti equazioni differenziali:

$I_{R}={\frac {V_{in}}{R}}$

e

$I_{C}=C{\frac {dV_{in}}{dt}}$.

Per un ingresso a gradino (in altre parole, applicando un segnale in corrente continua), la derivata dell'ingresso è un impulso all'istante in cui viene applicato il segnale ($t=0$). Quindi, la capacità si carica completamente in tempi molto rapidi e poi si comporta come un circuito aperto (l'usuale comportamento a regime continuo di una capacità).

Voci correlate

• RL circuit
• LC circuit
• RLC circuit
• Electrical network
• List of electronics topics

External links

• RC Filter Calculator

{Fonte