Polígono
Este artigo precisa de máis fontes ou referencias que aparezan nunha publicación acreditada que poidan verificar o seu contido, como libros ou outras publicacións especializadas no tema. Por favor, axude mellorando este artigo. |
| Polígonos | ||
|---|---|---|
| Nome | Número de lados | |
| monógono[1] | 1 | |
| dígono[2] | 2 | |
| triángulo | 3 | |
| cuadrilátero | 4 | |
| pentágono | 5 | |
| hexágono | 6 | |
| heptágono | 7 | |
| octógono | 8 | |
| enneágono | 9 | |
| decágono | 10 | |
| hendecágono | 11 | |
| dodecágono | 12 | |
| tridecágono | 13 | |
| tetradecágono | 14 | |
| pentadecágono | 15 | |
| hexadecágono | 16 | |
| heptadecágono | 17 | |
| octodecágono | 18 | |
| eneadecágono | 19 | |
| isodecágono | 20 | |
| triacontágono | 30 | |
| tetracontágono | 40 | |
| pentacontágono | 50 | |
| hexacontágono | 60 | |
| heptacontágono | 70 | |
| octacontágono | 80 | |
| eneacontágono | 90 | |
| hectágono | 100 | |
| chiliágono | 1000 | |
| miriágono | 10 000 | |
| megágono | 1 000 000 | |
Un polígono é unha figura plana limitada por unha liña poligonal pechada sen interseccións entre os segmentos que a forman (exceptuando vértices extremos). O polígono será regular se tódolos lados teñen a mesma lonxitude e tódolos ángulos internos son iguais, e será irregular noutro caso. Os polígonos teñen o mesmo número de lados que de ángulos (por omisión, ó falar de ángulos dun polígono acostumamos referirnos só ós ángulos internos, referencia asumida na afirmación anterior).
Se n é o número de lados, o número de diagonais dun polígono está dado por .
Etimoloxía
[editar | editar a fonte]A verba polígono procede do grego antigo πολύγωνον (polygōnon), de poli (πολύς), "moitos" e gonos (γωνία), "ángulo".
Clasificación dos polígonos
[editar | editar a fonte]Os polígonos clasifícanse polo número dos seus lados como se ve na táboa da dereita.
Pola forma do seu contorno debúllase a seguinte clasificación:
|
- simple, se dúas das súas arestas non consecutivas non se cortan,
- complexo, se dúas das súas arestas non consecutivas se cortan;
- convexo, se ao atravesalo unha recta córtao nun máximo de dous puntos,
- cóncavo, se ao atravesalo unha recta pode cortalo en máis de dous puntos;
- regular, se ten os seus ángulos e os seus lados iguais,
- irregular, se ten os seus ángulos e lados desiguais;
- equilátero, o que ten todos os seus lados iguais,
- equiángulo, o que ten todos os seus ángulos iguais.
- rectilíneo, se todos os seus lados son segmentos rectos,
- curvilíneo, se polo menos un dos seus lados é un segmento curvo.
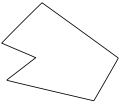
-
Polígono simple, cóncavo, irregular.
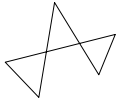
-
Polígono complexo, cóncavo, irregular.
-
Polígono convexo, regular (equilátero e equiángulo).
Polígonos regulares
[editar | editar a fonte]

Os polígonos que teñen tódolos seus lados coa mesma lonxitude e todos os seus ángulos iguales chámanse polígonos regulares. A área dun polígono regular pode ser calculada da seguinte forma: Supoñendo que:
A = Área
n = número de lados
l = lonxitude dun dos lados
a = apotema
Cúmprense as seguintes relacións:
Polígonos irregulares
[editar | editar a fonte]
Os polígonos irregulares son aqueles que non teñen tódolos lados e ángulos iguais. O cálculo da área dun polígono irregular pódese facer dividíndoo en polígonos menores (habitualmente triángulos), sendo a superficie total a suma das áreas de todos eles. Se o polígono é regular, este cálculo é , sendo p o seu perímetro (igual ó número de lados pola lonxitude dun deles) e a o apotema.
Notas
[editar | editar a fonte]Véxase tamén
[editar | editar a fonte]Ligazóns externas
[editar | editar a fonte]| Wikimedia Commons ten máis contidos multimedia na categoría: Polígono |
- Polígono, en webdelprofesor.ula.ve Arquivado 28 de xaneiro de 2010 en Wayback Machine. (en castelán)
- Eric W. Weisstein, Polygon at MathWorld. (en inglés)
- Geometria: Polígonos e triângulos (en portugués)