Detection of the Coupling between Vegetation Leaf Area and Climate in a Multifunctional Watershed, Northwestern China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. LAI Dataset
2.3. Climate and Aridity Index Data
2.4. EOF and SVD Analysis
3. Results
3.1. EOF Patterns of Annual AI
3.2. EOF Patterns of Annual LAI
3.2.1. General Spatial Characteristics
3.2.2. Regional Spatial Characteristics
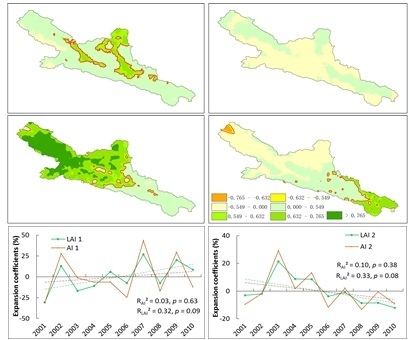
3.3. SVD Coupling Patterns
3.3.1. Annual Patterns of 1983–2000
3.3.2. Annual Patterns for the 2001–2010
3.3.3. Monthly Patterns
3.4. Grazing History
4. Discussion
4.1. Effects of AI on the Increase in Vegetation LAI
4.2. Potential Extreme Climate Effect on LAI
4.3. Other Factors Affecting LAI
4.4. Regional Implications
4.5. Uncertainties
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Sun, G.; Feng, X.; Xiao, J.; Shiklomanov, A.; Wang, S.; Zhang, Z.; Lu, N.; Wang, S.; Chen, L.; Fu, B.; et al. Impacts of global change on water resources in dryland East Asia. In Dryland East Asia: Land Dynamics Amid Social and Climate Change; Chen, J., Wan, S., Henebry, G., Qi, J., Gutman, G., Sun, G., Kappas, M., Eds.; HEP & De Gruyter: Berlin, Germany, 2013; pp. 153–182. [Google Scholar]
- Sun, G.; Liu, Y. Forest influences on climate and water resources at the landscape to regional scale. In Landscape Ecology for Sustainable Environment and Culture; Fu, B., Jones, K.B., Eds.; Springer: Berlin, Germany, 2013; pp. 309–334. [Google Scholar]
- Krishnaswamy, J.; John, R.; Joseph, S. Consistent response of vegetation dynamics to recent climate change in tropical mountain regions. Glob. Chang. Biol. 2014, 20, 203–215. [Google Scholar] [CrossRef] [PubMed]
- Roerink, G.J.; Menenti, M.; Soepboer, W.; Su, Z. Assessment of climate impact on vegetation dynamics by using remote sensing. Phys. Chem. Earth 2003, 28, 103–109. [Google Scholar] [CrossRef]
- Xiao, J.; Zhou, Y.; Zhang, L. Contributions of natural and human factors to increases in vegetation productivity in China. Ecosphere 2015, 6, 1–20. [Google Scholar] [CrossRef]
- Piao, S.; Yin, G.; Tan, J.; Cheng, L.; Huang, M.; Li, Y.; Liu, R.; Mao, J.; Myneni, R.B.; Peng, S.; et al. Detection and attribution of vegetation greening trend in China over the last 30 years. Glob. Chang. Biol. 2015, 21, 1601–1609. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Shen, Y.; Hu, R. Preliminary study on signal, impact and foreground of climatic shift from warm–dry to warm-humid in northwest China. J. Glaciol. Geocryol. 2002, 24, 219–226. [Google Scholar]
- Shi, Y.; Shen, Y.; Li, D.; Zhang, G.; Ding, Y.; Hu, J.; Kang, E. Discussion on the present climate change from warm–dry to warm–wet in northwest China. Quat. Sci. 2003, 23, 152–164. [Google Scholar]
- Kang, S.; Xu, Y.; You, Q.; Flugel, W.A.; Pepin, N.; Yao, T. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 8. [Google Scholar] [CrossRef]
- Donohue, R.J.; Mcvicar, T.R.; Roderick, M.L. Climate-related trends in australian vegetation cover as inferred from satellite observations, 1981–2006. Glob. Chang. Biol. 2009, 15, 1025–1039. [Google Scholar] [CrossRef]
- Zhang, L.X.; Zhou, D.C.; Fan, J.W.; Hu, Z.M. Comparison of four light use efficiency models for estimating terrestrial gross primary production. Ecol. Model. 2015, 300, 30–39. [Google Scholar] [CrossRef]
- Chen, L.; Tian, H.; Fu, B.; Zhao, X. Development of a new index for integrating landscape patterns with ecological processes at watershed scale. Chin. Geogr. Sci. 2009, 19, 37–45. [Google Scholar] [CrossRef]
- Benčoková, A.; Krám, P.; Hruška, J. The impact of climate change on hydrological patterns in Czech headwater catchments. Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 1245–1278. [Google Scholar] [CrossRef]
- Cutter, S.L.; Renwick, W.H. Exploitation, Conservation, Preservation: A Geographic Perspective on Natural Resource Use, 4nd ed.; John Wiley & Son: New York, NY, USA, 2003; p. 376. [Google Scholar]
- Qi, S.; Luo, F. Water environmental degradation of the Heihe River Basin in arid northwestern China. Environ. Monit. Assess. 2005, 108, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Qi, S.; Luo, F. Environmental degradation problems in the Heihe River Basin, northwest China. Water Environ. J. 2007, 21, 142–148. [Google Scholar] [CrossRef]
- Wang, G.; Cheng, G. Water resource development and its influence on the environment in arid areas of China—The case of the Hei River Basin. J. Arid Environ. 1999, 43, 121–131. [Google Scholar]
- Li, X.; Lu, L.; Cheng, G.; Xiao, H. Quantifying landscape structure of the Heihe River Basin, northwest China using FRAGSTATS. J. Arid Environ. 2001, 48, 521–535. [Google Scholar] [CrossRef]
- Yang, D.; Bing, G.; Yang, J.; Lei, H.; Zhang, Y.; Yang, H.; Cong, Z. A distributed scheme developed for eco-hydrological modeling in the upper Heihe River. Sci. China Earth Sci. 2015, 58, 36–45. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, D.; Sun, Y.; Liu, X.; Wang, N.; Savenije, H.H.G. Water demand management: A case study of the Heihe River Basin in China. Phys. Chem. Earth 2005, 30, 408–419. [Google Scholar] [CrossRef]
- Gao, B.; Qin, Y.; Wang, Y.; Yang, D.; Zheng, Y. Modeling ecohydrological processes and spatial patterns in the upper Heihe Basin in China. Forests 2016, 7. [Google Scholar] [CrossRef]
- Zhou, J.; Cai, W.; Qin, Y.; Lai, L.; Guan, T.; Zhang, X.; Jiang, L.; Du, H.; Yang, D.; Cong, Z. Alpine vegetation phenology dynamic over 16 years and its covariation with climate in a semi-arid region of China. Sci. Total Environ. 2016, 572, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Kang, E.; Lu, L.; Xu, Z. Vegetation and carbon sequestration and their relation to water resources in an inland river basin of Northwest China. J. Environ. Manag. 2007, 85, 702–710. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Shi, Q.; Zhang, Q.; Shi, C.; Yin, F. Impacts of land use and land cover changes on surface energy and water balance in the Heihe River Basin of China, 2000–2010. Phys. Chem. Earth 2015, 79–82, 2–10. [Google Scholar] [CrossRef]
- Wang, Z.X.; Liu, C.; Alfredo, H. From AVHRR–NDVI to MODIS–EVI: Advances in vegetation index research. Acta Ecol. Sin. 2003, 23, 979–987. [Google Scholar]
- Yang, J.; Guo, N.; Huang, L.N.; Jia, J.H. Ananlyses on MODIS NDVI index saturation in northwest China. Plateau Meteorol. 2008, 27, 896–903. [Google Scholar]
- Zhou, Y.; Tang, S.; Zhu, Q.; Li, J.; Sun, R.; Liu, S. Measurement of LAI in Changbai mountains nature reserve and its result. Resour. Sci. 2003, 25, 38–42. [Google Scholar]
- Tong, X.; Wang, K.; Brandt, M.; Yue, Y.; Liao, C.; Fensholt, R. Assessing future vegetation trends and restoration prospects in the karst regions of southwest China. Remote Sens. 2016, 8, 357. [Google Scholar] [CrossRef]
- Fensholt, R.; Rasmussen, K.; Nielsen, T.T.; Mbow, C. Evaluation of earth observation based long term vegetation trends–Intercomparing NDVI time series trend analysis consistency of Sahel from AVHRR GIMMS, Terra MODIS and SPOT VGT data. Remote Sens. Environ. 2009, 113, 1886–1898. [Google Scholar] [CrossRef]
- Xiong, Z.; Yan, X. Building a high–resolution regional climate model for the Heihe River Basin and simulating precipitation over this region. Chin. Sci. Bull. 2013, 58, 4670–4678. [Google Scholar] [CrossRef]
- Wang, Y.; Law, R.M.; Park, B. A global model of carbon, nitrogen and phosphorus cycles for the terrestrial biosphere. Biogeosciences 2010, 7, 2261–2282. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.L.; Levis, S.; Sakaguchi, K. Parameterization improvements and functional and structural advances in version 4 of the community land model. J. Adv. Model. Earth Syst. 2011, 3, 365–375. [Google Scholar]
- Krinner, G.; Viovy, N.; Noblet-Ducoudré, N.D.; Ogée, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19, 56. [Google Scholar] [CrossRef]
- Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
- Zeng, N.; Qian, H.; Roedenbeck, C.; Heimann, M. Impact of 1998–2002 midlatitude drought and warming on terrestrial ecosystem and the global carbon cycle. Geophys. Res. Lett. 2005, 32, 45–81. [Google Scholar] [CrossRef]
- Kim, J.B.; Monier, E.; Sohngen, B.; Pitts, G.S.; Drapek, R.; Ohrel, S.; Cole, J. Simulating Climate Change Impacts on Major Global Forestry Regions under Multiple Socioeconomic and Emissions Scenarios; Working Paper; US Forest Service, Pacific Northwest Laboratories: Portland, OR, USA, 2015. [Google Scholar]
- Bretherton, C.S.; Smith, C.; Wallace, J.M. An intercomparison of methods for finding coupled patterns in climate data. J. Clim. 1992, 5, 541–560. [Google Scholar] [CrossRef]
- Wallace, J.M.; Smith, C.; Bretherton, C.S. Singular value decomposition of wintertime sea surface temperature and 500–mb height anomalies. J. Clim. 1992, 5, 561–576. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Zheng, Y. 1:100000 Vegetation Map of Heihe River Basin (Version 2.0); Cold and Arid Regions Science Data Center: Lanzhou, China, 2016. [Google Scholar]
- Zhao, C.; Nan, Z.; Cheng, G. Methods for modelling of temporal and spatial distribution of air temperature at landscape scale in the southern Qilian mountains, China. Ecol. Model. 2005, 189, 209–220. [Google Scholar]
- BNU Center for Global Change Data Processing and Analysis. Available online: http://www.bnu-datacenter.com/ (accessed on 16 January 2016).
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X. Leaf Area Index retrieval from multi-sensor remote sensing data using general regression neural networks. IEEE Trans. Geosci. Remote 2013, 43, 1855–1865. [Google Scholar]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-time-series global land surface satellite leaf area index product derived from MODIS and AVHRR surface reflectance. IEEE Trans. Geosci. Remote 2016, 54, 1–18. [Google Scholar] [CrossRef]
- Budyko, M. Climate and Life; Academic Press: New York, NY, USA, 1974; p. 508. [Google Scholar]
- Kingston, D.G.; Todd, M.C.; Taylor, R.G.; Thompson, J.R.; Arnell, N.W. Uncertainty in the estimation of potential evapotranspiration under climate change. Geophys. Res. Lett. 2009, 36, 1437–1454. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Federer, C.A.; Schloss, A.L. Potential evaporation functions compared on US watersheds: Possible implications for global-scale water balance and terrestrial ecosystem modeling. J. Hydrol. 1998, 207, 147–169. [Google Scholar]
- Lu, J.; Sun, G.; Mcnulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the southeastern United States. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Hamon, W.R. Computation of Direct Runoff Amounts from Storm Rainfall; International Association of Scientific Hydrology Publication: Wallingford, DC, USA, 1963; pp. 52–62. [Google Scholar]
- Ponce, V.M.; Pandey, R.P.; Ercan, S. Characterization of drought across climatic spectrum. J. Hydrol. Eng. 2000, 5, 222–224. [Google Scholar] [CrossRef]
- Xiong, Z.; Fu, C.B.; Yan, X.D. Regional integrated environmental model system and its simulation of East Asia summer monsoon. Sci. Bull. 2009, 54, 4253–4261. [Google Scholar] [CrossRef]
- Zhao, D.M.; Fu, C.B.; Yan, X.D. Testing the ability of RIEMS2.0 to simulate multi-year precipitation and air temperature in China. Sci. Bull. 2009, 54, 3101–3111. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Henderson-Sellers, A.; Kennedy, P.J. Biosphere-Atmosphere Transfer Scheme (BATS) Version as Coupled to the NCAR Community Climate Model; NCAR Technical Report, NCAR/TN-387+STR; National Center for Atmospheric Research: Boulder, CO, USA, 1993. [Google Scholar]
- Grell, G.A. Prognostic evaluation of assumptions used by cumulus parameterizations. Mon. Weather Rev. 1993, 121, 764–787. [Google Scholar] [CrossRef]
- Fritsch, J.M.; Chappell, C.F. Numerical prediction of convectively driven mesoscale pressure systems. Part I: Convective parameterization. J. Atmos. Sci. 1964, 37, 198–202. [Google Scholar] [CrossRef]
- Kiehl, J.T.; Hack, J.J.; Bonan, G.B.; Boville, B.A.; Briegleb, B.P.; Williamson, D.L.; Rasch, P.J. Description of the NCAR Community Climate Model (CCM3); Technical Report, NCAR/TN-420+STR; National Center for Atmospheric Research: Boulder, CO, USA, 1996. [Google Scholar]
- Hannachi, A.; Jolliffe, I.; Stephenson, D. Empirical orthogonal functions and related techniques in atmospheric science: A review. Int. J. Climatol. 2007, 27, 1119–1152. [Google Scholar] [CrossRef]
- Liu, Y. Prediction of monthly-seasonal precipitation using coupled SVD patterns between soil moisture and subsequent precipitation. Geophys. Res. Lett. 2003, 30, 91–117. [Google Scholar] [CrossRef]
- Liu, Y. Spatial patterns of soil moisture connected to monthly-seasonal precipitation variability in a monsoon region. J. Geophys. Res. 2003, 108, 1981–1990. [Google Scholar] [CrossRef]
- Wu, H.; Wu, L. Methods for Diagnosing and Forecasting Climate Variability; Meteorological Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Zhang, Z.T.; Liu, Q. Rangeland Resources of the Major Livestock Regions in China and Their Development and Utilization; Science and Technology Press: Beijing, China, 1992; pp. 15–116. (In Chinese) [Google Scholar]
- Sa, W. Study on Dynamic of Grassland Productivities and Carring Capacity on the Alpine Grassland of Qinhai-Tibetan Plateau. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2012. [Google Scholar]
- Liu, Y.; Xiao, J.; Ju, W.; Xu, K.; Zhou, Y.; Zhao, Y. Recent trends in vegetation greenness in China significantly altered annual evapotranspiration and water yield. Environ. Res. Lett. 2016. [Google Scholar] [CrossRef]
- Angert, A.; Biraud, S.; Bonfils, C.; Henning, C.; Buermann, W.; Pinzon, J.; Tucker, C.; Fung, I. Drier summers cancel out the CO2 uptake enhancement induced by warmer springs. Proc. Natl. Acad. Sci. USA 2005, 102, 10823–10827. [Google Scholar] [CrossRef] [PubMed]
- Goetz, S.J.; Bunn, A.G.; Fiske, G.J.; Houghton, R. Satellite-observed photosynthetic trends across boreal north America associated with climate and fire disturbance. Proc. Natl. Acad. Sci. USA 2005, 102, 13521–13525. [Google Scholar] [CrossRef] [PubMed]
- Piao, S.; Wang, X.; Ciais, P.; Zhu, B.; Wang, T.; Liu, J. Changes in satellite-derived vegetation growth trend in temperate and boreal Eurasia from 1982 to 2006. Glob. Chang. Biol. 2011, 17, 3228–3239. [Google Scholar] [CrossRef]
- Wang, X.; Piao, S.; Ciais, P.; Li, J.; Friedlingstein, P.; Koven, C.; Chen, A. Spring temperature change and its implication in the change of vegetation growth in north America from 1982 to 2006. Proc. Natl. Acad. Sci. USA 2011, 108, 1240–1245. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Chen, H.; Levy, J.K. Spatiotemporal vegetation cover variations in the Qinghai-Tibet Plateau under global climate change. Chin. Sci. Bull. 2008, 53, 915–922. [Google Scholar] [CrossRef]
- Li, H.; Liu, G.; Fu, B. Response of vegetation to climate change and human activity based on NDVI in the Three-River Headwaters region. Acta Ecol. Sin. 2011, 31, 5495–5504. [Google Scholar]
- Niemand, C.; Köstner, B.; Prasse, H.; Grünwald, T.; Bernhofer, C. Relating tree phenology with annual carbon fluxes at tharandt forest. Meteorol. Z. 2005, 14, 197–202. [Google Scholar] [CrossRef]
- Wu, D.; Xiang, Z.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag effects of global vegetation responses to climate change. Glob. Chang. Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef] [PubMed]
- Rundquist, B.C.; Harrington, J.A., Jr. The effects of climatic factors on vegetation dynamics of tallgrass and shortgrass cover. Geocarto Int. 2000, 15, 33–38. [Google Scholar] [CrossRef]
- Edenhofer, O.; Pichsmadruga, R.; Sokona, Y.; Farahani, E.; Kadner, S.; Seyboth, K.; Adler, A.; Baum, I.; Brunner, S.; Eickemeier, P.; et al. IPCC, 2014: Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2015. [Google Scholar]
- Knapp, A.K.; Beier, C.; Briske, D.D.; Classen, A.T.; Luo, Y.; Reichstein, M.; Smith, M.D.; Smith, S.D.; Bell, J.E.; Fay, P.A. Consequences of more extreme precipitation regimes for terrestrial ecosystems. Bioscience 2008, 58, 811–821. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, J.; Ju, W.; Zhou, Y.; Wang, S.; Wu, X. Water use efficiency of china's terrestrial ecosystems and responses to drought. Sci. REP-UK 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.M. Analysis and assessment of the risk of snow and freezing disaster in China. Int. J. Disaster Risk Reduct. 2016. [Google Scholar] [CrossRef]
- Duan, A.; Wu, G.; Zhang, Q.; Liu, Y. New proofs of the recent climate warming over the Tibetan Plateau as a result of the increasing greenhouse gases emissions. Chin. Sci. Bull. 2006, 51, 1396–1400. [Google Scholar] [CrossRef]
- Li, C.; Kang, S. Review of studies in climate change over the Tibetan Plateau. Acta Geogr. Sin. 2006, 61, 327–335. (In Chinese) [Google Scholar]
- Liu, X.; Cheng, Z.; Yan, L.; Yin, Z. Elevation dependency of recent and future minimum surface air temperature trends in the Tibetan Plateau and its surroundings. Glob. Planet. Chang. 2009, 68, 164–174. [Google Scholar] [CrossRef]
- Adams, H.D.; Guardiolaclaramonte, M.; Barrongafford, G.A.; Villegas, J.C.; Breshears, D.D.; Zou, C.B.; Troch, P.A.; Huxman, T.E. Temperature sensitivity of drought-induced tree mortality portends increased regional die-off under global-change-type drought. Proc. Natl. Acad. Sci. USA 2009, 106, 7063–7066. [Google Scholar] [CrossRef] [PubMed]
- Griffin, D.; Anchukaitis, K.J. How unusual is the 2012–2014 California drought? Geophys. Res. Lett. 2014, 41, 9017–9023. [Google Scholar] [CrossRef]
- Williams, A.P.; Allen, C.D.; Macalady, A.K.; Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D. Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Chang. 2013, 3, 292–297. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; Mcdowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H. A global overview of drought and heat–induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Anthony, D.A.; Roger, P.P.; Chris, D.; Jiebu; Zhang, Y.; Lin, H. Livestock grazing, plateau pikas and the conservation of avian biodiversity on the Tibetan plateau. Biol. Conserv. 2008, 141, 1972–1981. [Google Scholar]
- Qin, Y.; Chen, J.; Yi, S. Plateau pikas burrowing activity accelerates ecosystem carbon emission from alpine grassland on the Qinghai-Tibetan plateau. Ecol. Eng. 2015, 84, 287–291. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Ji, X. Variations of glaciers in the Yeniugou watershed of Heihe River Basin from 1956 to 2003. J. Glaciol. Geocryol. 2007, 29, 100–106. [Google Scholar]
- Lin, L.; Jin, H.; Luo, D.; Lu, L.; He, R.X. Preliminary study on major features of alpine vegetation in the Source Area of the Yellow River (SAYR). J. Glaciol. Geocryol. 2014, 36, 230–236. [Google Scholar]
- Hu, B.; Cao, G.; Ma, Y.; Li, J.; Wei, J. The dynamic monitoring and analysis on driving force of wetland based on GIS and RS-Taking the Yeniugou river (upstream) as a case. Remote Sens. Inf. 2011, 6, 98–102. (In Chinese) [Google Scholar]
- Wu, J. The effect of ecological management in the upper reaches of Heihe River. Acta Ecol. Sin. 2011, 31, 1–7. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Hao, L.; Sun, G.; Liu, Y.; Gao, Z.; He, J.; Shi, T.; Wu, B. Effects of precipitation on grassland ecosystem restoration under grazing exclusion in inner Mongolia, China. Landsc. Ecol. 2014, 29, 1657–1673. [Google Scholar] [CrossRef]
- Xiang, Y.; Xiao, Z.; Liang, S.; Wang, J.; Song, J. Validation of Global Land Surface Satellite (GLASS) leaf area index product. J. Remote Sens. 2014, 18, 573–596. [Google Scholar]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global Land Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Gong, D.; Shi, P.; He, X. Spatial features of the coupling between spring NDVI and temperature over northern hemisphere. Acta Ecol. Sin. 2002, 57, 505–514. [Google Scholar]
- Dietz, M.E.; Clausen, J.C. Stormwater runoff and export changes with development in a traditional and low impact subdivision. J. Environ. Manag. 2008, 87, 560–566. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Chen, J.; Xia, J.; Li, L. Grazing and watering alter plant phenological processes in a desert steppe community. Plant Ecol. 2015, 216, 599–613. [Google Scholar] [CrossRef]














| Periods | Parameters | Mode 1 | Mode 2 |
|---|---|---|---|
| 1983–2010 | V 1 | 77.0% | 8.3% |
| CV 2 | 77.0% | 85.3% |
| Periods | Parameters | Mode 1 | Mode 2 | Mode 3 | Mode 4 |
|---|---|---|---|---|---|
| 1983–2000 | V 1 | 26.0% | 15.2% | 8.0% | 6.4% |
| CV 2 | 26.0% | 41.2% | 49.2% | 55.6% | |
| 2001–2010 | V 1 | 35.9% | 13.8% | 11.2% | 8.8% |
| CV 2 | 35.9% | 49.7% | 60.9% | 69.7% |
| Periods | Modes | 1 | SCF 2 | CSCF 3 | CLAI 4 | R 5 |
|---|---|---|---|---|---|---|
| 1983–2000 | 1 | 257.8 | 85.8 | 85.8 | 17.5 | 0.72 |
| 2 | 61.4 | 4.9 | 90.7 | 11.3 | 0.74 | |
| 2001–2010 | 1 | 337.5 | 80.9 | 80.9 | 31.1 | 0.83 |
| 2 | 106.1 | 8.0 | 88.9 | 10.0 | 0.89 |
| Periods | Modes | 1 | SCF 2 | CSCF 3 | CLAI 4 | R 5 |
|---|---|---|---|---|---|---|
| 1983–2000 | 1 | 135.5 | 91.0 | 91.0 | 16.2 | 0.39 |
| 2 | 24.9 | 3.1 | 94.0 | 6.1 | 0.41 | |
| 3 | 18.1 | 1.6 | 95.6 | 4.6 | 0.59 | |
| 2001–2010 | 1 | 117.7 | 80.7 | 80.7 | 17.1 | 0.36 |
| 2 | 41.5 | 10.0 | 90.7 | 4.8 | 0.55 | |
| 3 | 22.1 | 2.9 | 93.6 | 5.3 | 0.49 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, L.; Pan, C.; Liu, P.; Zhou, D.; Zhang, L.; Xiong, Z.; Liu, Y.; Sun, G. Detection of the Coupling between Vegetation Leaf Area and Climate in a Multifunctional Watershed, Northwestern China. Remote Sens. 2016, 8, 1032. https://doi.org/10.3390/rs8121032
Hao L, Pan C, Liu P, Zhou D, Zhang L, Xiong Z, Liu Y, Sun G. Detection of the Coupling between Vegetation Leaf Area and Climate in a Multifunctional Watershed, Northwestern China. Remote Sensing. 2016; 8(12):1032. https://doi.org/10.3390/rs8121032
Chicago/Turabian StyleHao, Lu, Cen Pan, Peilong Liu, Decheng Zhou, Liangxia Zhang, Zhe Xiong, Yongqiang Liu, and Ge Sun. 2016. "Detection of the Coupling between Vegetation Leaf Area and Climate in a Multifunctional Watershed, Northwestern China" Remote Sensing 8, no. 12: 1032. https://doi.org/10.3390/rs8121032
APA StyleHao, L., Pan, C., Liu, P., Zhou, D., Zhang, L., Xiong, Z., Liu, Y., & Sun, G. (2016). Detection of the Coupling between Vegetation Leaf Area and Climate in a Multifunctional Watershed, Northwestern China. Remote Sensing, 8(12), 1032. https://doi.org/10.3390/rs8121032