Two Decades of Terrestrial Water Storage Changes in the Tibetan Plateau and Its Surroundings Revealed through GRACE/GRACE-FO

Abstract

The Tibetan Plateau (TP) has the largest number of high-altitude glaciers on Earth. As a source of major rivers in Asia, this region provides fresh water to more than one billion people. Any terrestrial water storage (TWS) changes there have major societal effects in large parts of the continent. Due to the recent acceleration in global warming, part of the water environment in TP has become drastically unbalanced, with an increased risk of water disasters. We quantified secular and monthly glacier-mass-balance and TWS changes in water basins from April 2002 to December 2021 through the Gravity Recovery and Climate Experiment and its Follow-on satellite mission (GRACE/GRACE-FO). Adequate data postprocessing with destriping filters and gap filling and two regularization methods implemented in the spectral and space domain were applied. The largest glacier-mass losses were found in the Nyainqentanglha Mountains and Eastern Himalayas, with rates of −4.92 ± 1.38 Gt a⁻¹ and −4.34 ± 1.48 Gt a⁻¹, respectively. The Tien Shan region showed strong losses in its eastern and central parts. Furthermore, we found small glacier-mass increases in the Karakoram and West Kunlun. Most of the glacier mass change can be explained by snowfall changes and, in some areas, by summer rainfall created by the Indian monsoon. Major water basins in the north and south of the TP exhibited partly significant negative TWS changes. In turn, the endorheic region and the Qaidam basin in the TP, as well as the near Three Rivers source region, showed distinctly positive TWS signals related to net precipitation increase. However, the Salween River source region and the Yarlung Zangbo River basin showed decreasing trends. We suggest that our new and improved TWS-change results can be used for the maintenance of water resources and the prevention of water disasters not only in the TP, but also in surrounding Asian countries. They may also help in global change studies.

1. Introduction

The Tibetan Plateau (TP, Figure 1) is both the highest and the largest plateau in the world, and it contains many lakes and the largest ice fields outside of the Arctic and Antarctica. Therefore, it is regarded as ‘the water tower of Asia’. Any mass changes in Tibetan lakes and glaciers and other hydrological components (i.e., soil moisture, snow water, permafrost, and groundwater) are very sensitive to climate changes. The accurate monitoring of these basin-wide terrestrial water storage (TWS) changes and the analysis of their causes are indispensable for the proper utilization of regional water resources and understanding the global water cycle and the regional responses to climate change not only in the TP, but also its surrounding areas [1].

The climatic conditions in the TP and its surroundings experienced severe changes in recent decades due to global warming and changes in the atmospheric circulation patterns that are characterized by the Indian monsoon and the westerlies in the summer and winter, respectively, as well as the East Asian monsoon [2,3]. These led to changes in the TWS components, such as lake expansion [4,5], glacier retreat [6,7], permafrost degradation [8], and groundwater increases [9].

Figure 1. Map of the Tibetan Plateau and adjacent areas with topography based on Shuttle Radar Topography Mission (SRTM)’s digital elevation data [10]. Boundaries delineated by irregular shapes are glacier mascons and water basins based on the elevation basemap in this figure, provided by Xiang et al. [9]. White pixels denote glaciers taken from the Randolph Glacier Inventory 6.0 [11]. The glacier areas are divided into 14 mascons (mass-concentration blocks, black lines with black numbers): mascon 1, Nyainqentanglha; mascons 2 and 3, Eastern Himalayas; mascons 4 and 5, Western Himalayas; mascon 6, Karakoram; mascon 7, Hindukush; mascon 8, Pamir; mascons 9 to 12, Tien Shan; mascon 13, West Kunlun; and mascon 14, Qilian Mountains. Gray lines delimit water basins. ENDR is the endorheic region of the Tibetan Plateau (TP). White numbers mark river sources: (1) Yellow River, (2) Yangtze River, (3) Mekong River, (4) Salween River, and (5) Yarlung Zangbo River. Lakes are blue.

Figure 1. Map of the Tibetan Plateau and adjacent areas with topography based on Shuttle Radar Topography Mission (SRTM)’s digital elevation data [10]. Boundaries delineated by irregular shapes are glacier mascons and water basins based on the elevation basemap in this figure, provided by Xiang et al. [9]. White pixels denote glaciers taken from the Randolph Glacier Inventory 6.0 [11]. The glacier areas are divided into 14 mascons (mass-concentration blocks, black lines with black numbers): mascon 1, Nyainqentanglha; mascons 2 and 3, Eastern Himalayas; mascons 4 and 5, Western Himalayas; mascon 6, Karakoram; mascon 7, Hindukush; mascon 8, Pamir; mascons 9 to 12, Tien Shan; mascon 13, West Kunlun; and mascon 14, Qilian Mountains. Gray lines delimit water basins. ENDR is the endorheic region of the Tibetan Plateau (TP). White numbers mark river sources: (1) Yellow River, (2) Yangtze River, (3) Mekong River, (4) Salween River, and (5) Yarlung Zangbo River. Lakes are blue.

Many hydrological studies from the last decade focused on the components of TWS changes with various data and methods. However, due to its harsh weather conditions and challenging geography, in situ hydrology observations have rarely been made in the TP. Eventually, the Gravity Recovery and Climate Experiment (GRACE) twin-satellite mission became a very reliable tool to determine TWS changes [12]. Dedicated studies have been facilitated by the time-variable gravity measurements of GRACE since 2002. These are used to investigate general TWS changes at the whole-plateau scale and to compare the results from different GRACE solutions or post-processing filters [13,14] or monitor the regional mass changes individually [15,16,17,18]. The studies revealed that the TWS changes in the TP have changed not only dramatically but also inconsistently [14], whereas the nature of the heterogeneity of the TWS changes is still poorly understood [19]. An approach to increasing understanding is an investigation of TWS changes at the basin scale. The quantification of basin TWS changes would also be beneficial for the maintenance of local water resources.

Since the successful GRACE mission retired in 2017, 15 years after its launch, due to battery problems, the GRACE Follow-on (GRACE-FO) satellite mission launched in May 2018 has continued to provide gravity-field data. Unfortunately, an 11-month gap between GRACE (whose last product was obtain in June 2017) and GRACE-FO (whose first product was obtained in June 2018) emerged, impeding the continuous analysis of 20-year-long mass changes. Of the many efforts to bridge the gap [20,21,22,23,24], the Singular Spectrum Analysis (SSA) by Yi and Sneeuw [23] is considered the most appropriate for our purpose. The SSA is a non-parametric and data-adaptive method, which samples time series into time-lagged segments, obtains the correlation information, and then reconstructs the time series based on the temporal correlation. Hence, an analysis of a 20-year-long series of mass changes is enabled.

In this study, we investigate the TWS changes in the TP and its surroundings at the basin scale (Figure 1) and examine the spatio-temporal characteristics from 2002 to 2021, combining GRACE and GRACE-FO data with SSA-based gap filling. We therefore subdivide our study area into 700 mass-concentration blocks (mascons), some of which are of different sizes and shapes. Next to 14 glacier mascons (Figure 1), we analyze TWS changes in 10 water basins: Northwest India (NWIA), the Bengal basin (BBN), the Tarim basin (TRM), the Qaidam basin (QDM), the endorheic region (ENDR) of the TP, the Yellow River source (YLRS) region, the Yangtze River source (YZRS) region, the Mekong River source (MKRS) region, the Salween River source (SWRS) region, and the Yarlung Zangbo River (YZBR) basin. We thereby follow the postprocessing recommendations provided by Xiang et al. [14], who determined the best-performing filters for reliable TWS change results in the TP and its surroundings. In the next section, the data and processing-solution-filter combinations, as well as the calculation methodology, are briefly introduced. In Section 3, the results are presented with a corresponding detailed analysis, followed by a further discussion in Section 4. Finally, we summarize our findings in Section 5.

2. Data and Methodology

2.1. GRACE Data

More than 20 different monthly GRACE solutions, including spherical harmonics (SH) solutions and mascon models, have been released by different institutions. For extraction of the signal of interest, the SH solutions must be post-processed by the user before interpretation. Unwanted noise, especially because of so-called NS-directed stripes related to the orbital configuration of the GRACE satellite mission, can be reduced by adequate filtering. Following the recommendations of Xiang et al. [14] we use the SH solutions from the Institute of Geodesy (ITSG) at Graz University of Technology, Austria [25], and the Center for Space Research (CSR) at University of Texas, Austin [26], together with the ‘Duan P4M8’, ‘S&W P2M8’, and ‘S&W P3M8’ destriping filters (see Section 2.3).

The CM reference frame, with its origin at the Earth’s center of mass (CM), was used in the GRACE gravity-field determination [12]. In this frame, the degree one Stokes coefficient is undefined, and it can be defined with respect to the CF frame, with its origin at the center of figure (CF) of the Earth’s outer surface. The GRACE SH solution’s monthly Stokes coefficients are from 2 to 96 degrees. The degree-one Stokes coefficients can be estimated with the GRACE-OBP approach [27]. The C20 and C30 Stokes coefficients are subject to large uncertainties [28], presumably due to tide-like aliases, and thus need to be replaced with estimates from satellite laser ranging (SLR). Due to large higher degree/order (d/o) errors of Stokes coefficients [14], we set the d/o maximum to 60. In addition, the glacial isostatic adjustment (GIA) effects were removed from the monthly Stokes coefficients of the SH solutions, in accordance with the ICE-6G_C(VM5a) GIA model [29].

2.2. GLDAS Data

We used precipitation, snowfall, evaporation, and air temperature data of monthly and 1-degree-spatiotemporal-resolution Global Land Data Assimilation System (GLDAS)-Noah version 2.1 for climate-change analysis [30]. We verified the validity of GLDAS-Noah climate data by comparing precipitation parameters with Global Precipitation Climatology Project (GPCP) and Global Precipitation Climatology Centre (GPCC) data and found very consistent results.

The TP is far inland, with harsh weather conditions and challenging geography. In situ observations are rarely performed in this region. Although soil moisture data are provided by GLDAS, given that the glaciers are distributed on the alpine mountains, where effective monitoring is much scarcer and, thus, the soil-moisture changes from hydrological model are highly uncertain, we made a compromise and took those from GLDAS as uncertainty, and did not consider soil-moisture changes when estimating glacier-mass balance.

2.3. Gap Filling within GRACE Missions

After the GRACE data availability ended in June 2017, the GRACE-FO satellites provided the first product in June 2018, resulting in an 11-month gap. There were also isolated or paired small gaps, for various reasons, which created disturbances during the two missions, spanning a total of 24 months. These 35 months of gaps in total seriously impeded the continuous analysis of the 20-year-long observation of GRACE and GRACE-FO [23]. Therefore, we used the non-parametric and data-adaptive SSA technique of Yi and Sneeuw [23] to produce reasonable gap-filling results in the form of spherical harmonic coefficients (SHCs). The SSA first samples a time series into time-lagged segments. Next, the temporal correlation is determined, and it is used in the reconstruction of the time series.

2.4. Destriping Filters

We used the destriping methods proposed by Duan et al. [31] (Duan) and Swenson and Wahr [32] (S&W), namely filters ‘Duan P4M8’, ‘S&W P2M8’, and ‘S&W P3M8’, in combination with the two GRACE SH solutions of ITSG and CSR. They are found to perform best in the determination of TWS variations as they remove spatially correlated errors effectively [14]. The CSR with ‘S&W P2M8’ combination has a somewhat worse performance than the other five [14]; therefore, we applied five combinations in total.

2.5. Computation of Mass Changes

2.5.1. Calculation of SHCs-Derived TWS Change

If we denote the Stokes coefficients with their averages removed by $∆c_{lm}$ and $∆s_{lm}$, according to Wahr et al. [12], the mass change in equivalent water thickness (EWT) at any time and at an arbitrary site with co-latitude $\theta$ and longitude $\phi$ can be calculated by a synthesis of spherical harmonics,

$$∆EWT(\mathsf{\theta },\mathsf{\phi })=\frac{a{\rho }_{ave}}{3{\rho }_w}{\sum }_{l=0}^{l\mathrm{m}\mathrm{a}\mathrm{x}}{\sum }_{m=0}^l\frac{2l+1}{1+k_l}\times (∆c_{lm}\cos (m \phi )+∆s_{lm}\sin (m \phi )){\tilde{P}}_{lm}(\cos \theta ),$$

(1)

where $k_l$ is the degree $l$ elastic load Love number for potential perturbation. If a Gaussian filter is used, ${2\mathsf{\pi }\omega }_l$ should be inserted just before the second fraction. The ${\omega }_l$ is the degree coefficient of Jekeli’s Gaussian averaging function for Legendre expansion [33], ${\tilde{P}}_{lm}(\cos \theta )$ is the lth degree and mth order normalized associated Legendre polynomial $lmax=60$, the ${\rho }_{ave}$ is the average density of the Earth (5.517 g/cm³), ${\rho }_w$ is the water density (1 g/cm³), and $a$ is the average radius of the Earth.

2.5.2. Mascon Inverted Solution

Our study area contains a total number of $M$ = 700 independent mascons. The 14 glacier mascons with unregular shapes cover the large glacier mountains (Figure 1), based on the Randolph Glacier Inventory 6.0 (RGI) [11]. The other regions in the study area were divided into regular $2°\times 2°$ mascons, except the regions connecting the regular grid with the glacier mascons, which were also unregular mascons. Note that GRACE-derived mass changes in the glacier and non-glacier mascons were assumed to have been due to changes in glaciers only and all the hydrology components together, respectively.

If each mascon was covered by a uniformly distributed unit EWT ($m_j$), which can be decomposed into SH coefficients $\Delta {c\prime }_{lm}^j$ and $\Delta {s\prime }_{lm}^j$ ($j=1, 2, \cdots , M$) with Equations (3) and (4) by Xiang et al. [9] (except that $\Omega$ now represents the mascon region considered), according to Jacob et al. [34], the mass change (by EWT) can be computed for each mascon at any time with the spectral domain inverse (SEDI) [34,35] and the space domain inverse (SADI) [35].

The SEDI and SADI can be concisely expressed as

$$min{‖A^G-Bm‖}_2^2,$$

(2)

or

$$min{‖{YSA}^G-YSBm‖}_2^2,$$

(3)

where $A^G$ is a group of the changes in Stokes coefficient for a month or the secular trend of GRACE and GRACE-FO data, rewritten as ${({∆c}_{\mathrm{1,0}},∆c_{\mathrm{1,1}},\cdots ,{∆c}_{l,l},{∆s}_{\mathrm{1,1}},{∆s}_{\mathrm{2,1}},\cdots ,{∆s}_{l,l})}^{\mathrm{T}}$, excluding the coefficient for $l=0$, with a length of ${(l+1)}^2-1$, which is 3720 for the maximum $lmax$ = 60. $B$ is the matrix, with $B_{.,j}=A_j^{mas}$, and $A_j^{mas}$ is a column vector like $A^G$ but for the Stokes coefficients decomposed from the jth mascon. The $Y_{i,.}=({\tilde{P}}_{\mathrm{1,0}}^i, cos(1\phi ){\tilde{P}}_{\mathrm{1,1}}^i,\cdots , sin(1\phi ){\tilde{P}}_{11}^i,\cdots , sin(n\phi ){\tilde{P}}_{n,n}^i)$. The S is a diagonal matrix independent of observation with $S_{j,j}(l)=\frac{M_E}{a^2}{\omega }_l\frac{2l+1}{1+k_l}$. The ${\omega }_l$ is the degree coefficient of Jekeli’s Gaussian averaging function for Legendre expansion [33]; here, we use a 340 km averaging radius Gaussian smoothing filter to process the Stokes coefficients of the SH solutions, which basically correspond to the maximum d/o of 60 of GRACE data. The m is the column vector of M mascons with the mass of each mascon as $m_j$ ($j=1, 2, \cdots , \mathrm{M}$).

In the geophysical inversion, singularity is always a reverse problem, resulting in unstable and meaningless direct solutions. Thus, regularization methods are usually applied, such as the regularized iterative algorithm (RIA) method [36,37] and the Tikhonov regularization method [35,38].

For the RIA method, we build the regularization equation:

$$(B^{T}B+\alpha I)m^k=B^T{A}^G+\alpha m^{k-1},$$

(4)

where, $\alpha$ is a nonzero smoothing constant, $I$ is a unit matrix (in the same order as $B^{T}B$), and $k (=1,2,3,...)$ represents number of iterations. The vector m is assumed to converge to the true solution [37].

For the Tikhonov regularization method, we have

$$min\{{‖Bm-A^G‖}_2^2+{\alpha }^2{‖Im‖}_2^2\}.$$

(5)

Note that we also took into account the effect of a 340 km averaging radius Gaussian smoothing filter when implementing the inversion process with SEDI, by integrating ${\omega }_l$ with $A^G$ and $A_j^{mas}$ in the form of ${({{\omega }_1∆c}_{\mathrm{1,0}}, {\omega }_1∆c_{\mathrm{1,1}},\cdots ,{\omega }_l{∆c}_{l,l},{{\omega }_1∆s}_{\mathrm{1,1}}, {{\omega }_2∆s}_{\mathrm{2,1}},\cdots ,{{\omega }_l∆s}_{l,l})}^T$ and ${({\omega }_1∆{c\prime }_{\mathrm{1,0}}^j, {\omega }_1∆{c\prime }_{\mathrm{1,1}}^j,\cdots ,{\omega }_l∆{c\prime }_{l,l}^j,{\omega }_1∆{s\prime }_{\mathrm{1,1}}^j, {\omega }_2∆{s\prime }_{\mathrm{2,1}}^j,\cdots ,{\omega }_l∆{s\prime }_{l,l}^j)}^T$, respectively.

Taking the regularization methods of Equations (4) and (5) with SEDI, we can compute stable and appropriate solutions. Similarly, we can also implement regularization with SADI using Equations (6) and (7),

$$[{(YSB)}^{T}YSB+\alpha I]m^k={(YSB)}^T{YSA}^G+\alpha m^{k-1},$$

(6)

$$min\{{‖YSBm-YS{A}^G‖}_2^2+{\alpha }^2{‖Im‖}_2^2\}.$$

(7)

According to Yi and Sun [35], the SEDI contains all signals over the whole sphere, while the SADI filters out the signals outside the study region. To avoid this, a synthesis of TWS changes in study area was implemented and then decomposed into SH coefficients up to degree/order 60, providing $A^G$ used in Equations (4) to (7), referring to Xiang et al. [9]. We enlarged the area of concern outwards by 5 degrees, assuring that the data directly used for the inversion included as few leakage signals from outside of our study area as possible. Therefore, we calculated the TWS changes in TP and its surroundings using the RIA and Tikhonov regularization methods with both SEDI and SADI for the five selected SH solution-filter combinations mentioned above, for a total of 20 cases, to analyze the differences between them and to provide new, improved, and reliable TWS-change estimates.

2.6. Uncertainty Calculation

The errors of the trend results were determined from the measurement and inversion process. Therefore, the error can be given by four cases: (1) Since the accuracy of the GRACE solutions is mainly influenced by the measurements, the effects of the measurement-noise error were estimated by using the calculated mass change in the ocean at the same latitude but excluding ocean areas 1000 km from the continents to avoid land-signal leakage [39]. We mark this as ${\sigma }_{solution}$ here. (2) The secular trends were obtained by linear regression, which also provides corresponding regression errors, marked as ${\sigma }_{fit}$. (3) For the glacier mascons, we did not precisely separate soil moisture when estimating glacier-mass balance due to the extremely high uncertainty of soil moisture derived from hydrological models at alpine mascons covered by glaciers. For assessment of glacier change, we took the average soil-moisture-change rates from the three GLDAS models, NOAH, CLSM, and VIC, as errors, making corresponding estimates more robust. They are marked as ${\sigma }_{SM}$. (4) The five solution-filter combinations and two regularization methods were used with SEDI and SADI to determine the monthly mass changes and their trends. The average of the 20 different results was taken as the most effective result. To evaluate the uncertainty of the most effective results more robustly, we also considered the error of the inversion and average process and calculated the standard deviation of the 20 cases, marked as ${\sigma }_{process}$. Next, we applied the error sigma ($\sigma$) twice for uncertainty.

Finally, the error variance (${\sigma }_{TWS}^2$) for trend estimates of TWS changes can be calculated by

$${\sigma }_{TWS}^2={\sigma }_{solution}^2+{\sigma }_{fit}^2+{\sigma }_{SM}^2+{\sigma }_{process}^2,$$

(8)

where ${\sigma }_{TWS}$ represents the error in TWS changes in basins, as well as the errors in glacier-mass changes in glacier mascons. However, note that ${\sigma }_{SM}$ does not exist when evaluating the uncertainties in water basins, and ${\sigma }_{process}$ exists only for the averaged most effective results.

3. Results

The validity of the calculated monthly mass changes is discussed through an analysis of the similarities and differences between the destriping approaches, data sets, and regularization methods implemented in the spectral (SEDI) and the space domains (SADI). Note that the results are generally shown in gigatons per year (Gts a⁻¹) or millimeter EWT per year (mm a⁻¹) for the trends, and in gigatons (Gts) and by year (a) or month for the time series.

3.1. Effects of Destriping Filters and GRACE Data on SH Synthetic-Mass Changes

Due to signal-leakage effects, it is not encouraged to consider SH-synthetic-solution results as the most reliable. However, they perfectly represent GRACE-observed gravity changes after destriping, and thus play a decisive role in estimating the most accurate mascon solutions. Furthermore, it is very convenient to use SH-synthetic-solution results to show the effectiveness of destriping filters. In Figure 2, we show the mass-change trends in the TP and its surroundings derived from the monthly SH solutions for the five different destriping approaches to the processing of the ITSG and CSR SH solutions.

The N-S stripes were effectively depressed in the GRACE-derived trends. The results of the five GRACE solution-filter combinations showed strong agreement in their pattern and magnitude. For example, the negative signal of −45 to −49 mm a⁻¹ in Northwest India confirmed the excessive use of groundwater (e.g., Rodell et al. [40]; Long et al. [41]), while the negative signal of −19 mm a⁻¹ in the Tien Shan area (mascons 9–12) was caused by glacier melting [35,39]. The positive signal up to 16 mm a⁻¹ in the Three Rivers source region (south of mascon 14) is most likely to have been due to groundwater increase [9]. The anomalous gain in mass for Karakoram (mascon 6) [42,43,44,45,46] and the glacier-mass gain in West Kunlun (mascon 13) [47,48,49,50,51] are also clearly shown.

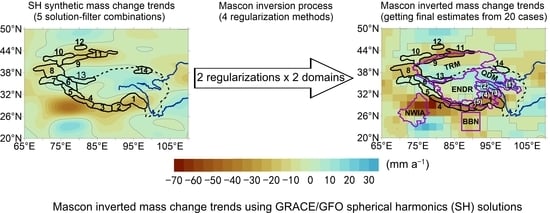
3.2. Effects of Inversion Processing on Mascon Inverted Mass Changes

Since the five combinations agreed very well and supported the post-processing suggestions of Xiang et al. [14], we applied the two regularization approaches both in the spectral (SEDI) and in the space domain (SADI) from Section 2.5.2 and calculated the mass changes from April 2002 to December 2021 at the mascon level. The results are shown in Figure 3, Figure 4, Figure 5, Figure A1 and Figure A2.

Figure 3 demonstrates that the 20 selected cases (2 regularizations × 2 domains × 5 solution-filter combinations) showed great similarities in signal pattern and magnitude, which was further confirmed with the Pearson’s correlation coefficient (PCC) values in

Table A1. Pearson’s correlation coefficients (PCC) among mass change trends from mascon inverted solutions shown in Figure 3.

PCC	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	p	q	r	s	t
a	1.00	0.98	1.00	0.99	0.98	0.96	0.98	0.98	0.97	0.95	0.97	0.97	0.99	0.96	0.99	0.98	0.97	0.94	0.97	0.96
b		1.00	0.97	0.99	0.96	0.98	0.95	0.97	0.94	0.97	0.94	0.95	0.97	0.99	0.96	0.97	0.95	0.97	0.94	0.96
c			1.00	0.99	0.98	0.95	0.98	0.97	0.97	0.94	0.97	0.96	0.99	0.95	0.99	0.97	0.97	0.94	0.98	0.96
d				1.00	0.98	0.97	0.97	0.98	0.96	0.95	0.95	0.97	0.99	0.97	0.98	0.98	0.97	0.95	0.96	0.97
e					1.00	0.98	1.00	0.99	0.99	0.96	0.98	0.98	0.97	0.94	0.97	0.96	0.99	0.96	0.99	0.98
f						1.00	0.97	0.99	0.96	0.99	0.95	0.97	0.95	0.97	0.95	0.96	0.97	0.99	0.96	0.97
g							1.00	0.99	0.98	0.96	0.99	0.98	0.97	0.93	0.98	0.95	0.99	0.95	0.99	0.97
h								1.00	0.98	0.97	0.97	0.98	0.97	0.95	0.97	0.97	0.99	0.97	0.98	0.98
i									1.00	0.98	1.00	0.99	0.96	0.93	0.96	0.95	0.98	0.94	0.98	0.96
j										1.00	0.97	0.98	0.94	0.96	0.94	0.95	0.96	0.97	0.95	0.96
k											1.00	0.99	0.96	0.92	0.97	0.94	0.98	0.94	0.98	0.96
l												1.00	0.96	0.94	0.96	0.95	0.98	0.95	0.97	0.97
m													1.00	0.97	1.00	0.99	0.98	0.96	0.98	0.97
n														1.00	0.96	0.99	0.96	0.98	0.95	0.97
o															1.00	0.98	0.98	0.95	0.98	0.97
p																1.00	0.97	0.97	0.96	0.98
q																	1.00	0.97	1.00	0.99
r																		1.00	0.96	0.99
s																			1.00	0.98
t																				1.00

Note: a–t for 20 cases are defined in Table 1.

. All the PCC values were larger than 0.90. The mascon inverted mass-change trends (Figure 3) confirmed the general signal features found in the SH solutions (Figure 2; see Section 3.1).

We investigated the effects of the regularization methods on the TWS time series of each selected glacier region and water basin. Figure 4 highlights the lack of an apparent difference between the time series from the four regularization cases for almost all the mascons. In mascon 14, Qilian Shan, the difference was slightly enhanced. This is likely to have been due to its small but fluctuating values around 0 in the time series and its location at the edge of a large signal pattern in the Tibetan Plateau (Figure 2 and Figure 3), which affected the mascon inverted solution here. The time series for the water basins in Figure 5 confirm the agreement between the different regularization methods.

We also obtained time-series results from the five solution-filter combinations, but only using the RIA regularization method with SEDI experiments (Figure A1 and Figure A2). There were visibly more, but still very minor differences in the time series. This confirmed that the destriping filters and GRACE data affected the results more than the chosen regularization method. This held for the trends, as well as the annual and semi-annual amplitudes.

3.3. Improved Mass Changes in Mascon Inverted Solutions

We show the results for every solution-filter-regularization combination in

Table 1. Mass-change trends in the 14 glacier mascons for the 20 solution-filter-regularization-combination cases (a–t) and their averaged trends (AVE). Units are in Gt a⁻¹.

No.		a	b	c	d	e	f	g	h	i	j	k
1	Nyainqentanglha	−4.77 ± 1.44	−4.73 ± 1.15	−4.82 ± 1.43	−4.73 ± 1.37	−5.09 ± 1.44	−5.05 ± 1.15	−5.15 ± 1.44	−5.05 ± 1.37	−4.76 ± 1.44	−4.74 ± 1.15	−4.80 ± 1.43
2	E. Himalayas	−2.21 ± 0.52	−2.09 ± 0.22	−2.24 ± 0.53	−2.08 ± 0.55	−1.89 ± 0.52	−1.79 ± 0.22	−1.92 ± 0.53	−1.77 ± 0.55	−1.72 ± 0.52	−1.62 ± 0.23	−1.75 ± 0.53
3		−2.10 ± 1.23	−2.16 ± 0.87	−2.09 ± 1.24	−2.18 ± 1.17	−2.36 ± 1.23	−2.46 ± 0.87	−2.35 ± 1.24	−2.48 ± 1.17	−2.88 ± 1.23	−2.95 ± 0.87	−2.88 ± 1.24
4	W. Himalayas	−2.08 ± 0.90	−1.96 ± 1.01	−2.14 ± 0.90	−1.93 ± 0.90	−1.91 ± 0.90	−1.79 ± 1.01	−1.93 ± 0.90	−1.79 ± 0.90	−1.88 ± 0.91	−1.77 ± 1.01	−1.93 ± 0.90
5		−0.45 ± 0.31	−0.46 ± 0.23	−0.43 ± 0.30	−0.48 ± 0.26	−0.26 ± 0.30	−0.24 ± 0.23	−0.24 ± 0.30	−0.26 ± 0.26	−0.16 ± 0.27	−0.17 ± 0.24	−0.14 ± 0.26
6	Karakoram	1.09 ± 0.29	1.08 ± 0.30	1.07 ± 0.29	1.11 ± 0.27	0.97 ± 0.30	0.93 ± 0.30	1.30 ± 0.30	0.95 ± 0.27	1.41 ± 0.29	1.37 ± 0.31	1.41 ± 0.29
7	Hindukush	0.43 ± 0.41	0.53 ± 0.33	0.38 ± 0.42	0.54 ± 0.38	−0.37 ± 0.42	−0.37 ± 0.33	−0.19 ± 0.43	−0.38 ± 0.38	0.06 ± 0.40	0.16 ± 0.34	−0.01 ± 0.41
8	Pamir	−2.13 ± 0.53	−2.29 ± 0.54	−2.11 ± 0.54	−2.20 ± 0.59	−1.68 ± 0.53	−1.82 ± 0.55	−1.52 ± 0.54	−1.71 ± 0.60	−1.83 ± 0.54	−2.03 ± 0.55	−1.78 ± 0.54
9	Tien Shan	−1.84 ± 0.35	−1.81 ± 0.24	−1.83 ± 0.34	−1.78 ± 0.34	−1.80 ± 0.36	−1.74 ± 0.24	−1.64 ± 0.35	−1.72 ± 0.34	−1.79 ± 0.37	−1.76 ± 0.24	−1.78 ± 0.37
10		−0.52 ± 0.57	−0.35 ± 0.51	−0.54 ± 0.56	−0.41 ± 0.52	−0.85 ± 0.57	−0.71 ± 0.51	−0.25 ± 0.57	−0.80 ± 0.52	−0.45 ± 0.60	−0.27 ± 0.51	−0.48 ± 0.60
11		−2.45 ± 0.35	−2.37 ± 0.08	−2.50 ± 0.36	−2.35 ± 0.16	−2.49 ± 0.35	−2.39 ± 0.08	−2.52 ± 0.36	−2.37 ± 0.16	−2.52 ± 0.37	−2.44 ± 0.08	−2.58 ± 0.37
12		−0.24 ± 0.12	−0.23 ± 0.06	−0.23 ± 0.12	−0.22 ± 0.03	−0.17 ± 0.11	−0.16 ± 0.06	−0.16 ± 0.11	−0.16 ± 0.03	−0.18 ± 0.10	−0.16 ± 0.06	−0.17 ± 0.10
13	West Kunlun	0.63 ± 0.16	0.64 ± 0.13	0.64 ± 0.16	0.60 ± 0.12	0.73 ± 0.17	0.80 ± 0.12	0.69 ± 0.17	0.77 ± 0.11	0.65 ± 0.16	0.69 ± 0.13	0.67 ± 0.15
14	Qilian	0.16 ± 0.05	0.13 ± 0.07	0.18 ± 0.05	0.10 ± 0.06	−0.03 ± 0.05	−0.03 ± 0.06	0.11 ± 0.05	−0.06 ± 0.06	0.04 ± 0.06	0.03 ± 0.06	0.08 ± 0.07
No.		l	m	n	o	p	q	r	s	t	AVE
1	Nyainqentanglha	−4.74 ± 1.37	−5.06 ± 1.44	−4.93 ± 1.16	−5.12 ± 1.43	−4.91 ± 1.38	−4.99 ± 1.43	−4.91 ± 1.16	−5.08 ± 1.43	−4.90 ± 1.38	−4.92 ± 1.38
2	E. Himalayas	−1.60 ± 0.55	−2.12 ± 0.52	−1.97 ± 0.23	−2.18 ± 0.53	−1.91 ± 0.55	−1.66 ± 0.52	−1.50 ± 0.23	−1.69 ± 0.53	−1.46 ± 0.55	−1.86 ± 0.65
3		−2.95 ± 1.17	−2.01 ± 1.24	−2.13 ± 0.87	−2.00 ± 1.24	−2.16 ± 1.17	−2.79 ± 1.24	−2.92 ± 0.87	−2.78 ± 1.24	−2.94 ± 1.17	−2.48 ± 1.33
4	W. Himalayas	−1.76 ± 0.90	−2.19 ± 0.90	−1.99 ± 1.01	−2.12 ± 0.90	−2.00 ± 0.90	−1.85 ± 0.90	−1.81 ± 1.01	−1.91 ± 0.90	−1.82 ± 0.90	−1.92 ± 0.96
5		−0.19 ± 0.26	−0.42 ± 0.28	−0.30 ± 0.25	−0.28 ± 0.28	−0.35 ± 0.27	0.03 ± 0.27	−0.03 ± 0.25	−0.08 ± 0.27	−0.08 ± 0.27	−0.24 ± 0.41
6	Karakoram	1.40 ± 0.28	1.19 ± 0.28	1.04 ± 0.31	1.03 ± 0.28	1.09 ± 0.28	1.40 ± 0.29	1.37 ± 0.31	1.40 ± 0.29	1.42 ± 0.28	1.18 ± 0.48
7	Hindukush	0.18 ± 0.39	0.22 ± 0.41	0.53 ± 0.34	0.37 ± 0.42	0.54 ± 0.38	0.06 ± 0.42	0.16 ± 0.34	−0.02 ± 0.42	0.19 ± 0.39	0.15 ± 0.76
8	Pamir	−1.94 ± 0.60	−2.03 ± 0.54	−2.35 ± 0.54	−2.14 ± 0.54	−2.26 ± 0.59	−1.84 ± 0.54	−2.06 ± 0.55	−1.79 ± 0.54	−1.99 ± 0.60	−1.99 ± 0.70
9	Tien Shan	−1.73 ± 0.34	−1.74 ± 0.35	−1.76 ± 0.24	−1.81 ± 0.35	−1.69 ± 0.34	−1.74 ± 0.36	−1.68 ± 0.24	−1.74 ± 0.35	−1.63 ± 0.35	−1.76 ± 0.35
10		−0.33 ± 0.52	−0.65 ± 0.56	−0.30 ± 0.51	−0.52 ± 0.56	−0.36 ± 0.52	−0.42 ± 0.57	−0.24 ± 0.51	−0.47 ± 0.56	−0.31 ± 0.52	−0.48 ± 0.68
11		−2.43 ± 0.16	−2.64 ± 0.33	−2.42 ± 0.09	−2.53 ± 0.35	−2.42 ± 0.17	−2.57 ± 0.33	−2.51 ± 0.08	−2.62 ± 0.35	−2.51 ± 0.17	−2.47 ± 0.38
12		−0.16 ± 0.03	−0.23 ± 0.11	−0.24 ± 0.06	−0.25 ± 0.11	−0.23 ± 0.03	−0.19 ± 0.10	−0.17 ± 0.06	−0.19 ± 0.10	−0.17 ± 0.03	−0.20 ± 0.13
13	West Kunlun	0.65 ± 0.12	0.57 ± 0.15	0.61 ± 0.13	0.61 ± 0.15	0.54 ± 0.12	0.63 ± 0.16	0.65 ± 0.13	0.63 ± 0.16	0.60 ± 0.12	0.65 ± 0.21
14	Qilian	0.04 ± 0.06	0.20 ± 0.05	0.16 ± 0.07	0.24 ± 0.06	0.13 ± 0.06	0.06 ± 0.05	0.03 ± 0.07	0.11 ± 0.06	0.01 ± 0.06	0.08 ± 0.17

Note: a–t in this table correspond to the 20 sub-figures in Figure 3, respectively. AVE represents the average of 20 cases. The uncertainties of AVE were evaluated with Equation (8) rather than the law of error propagation.

and

Table 2. As in Table 1, but with mass-change trends at 10 selected areas. Units are in Gt a⁻¹. NWIA: Northwest India; BBN: Bengal basin; TRM: Tarim basin; QDM: Qaidam basin; ENDR: endorheic region of the TP; YLRS: Yellow River source region; YZRS: Yangtze River source region; MKRS: Mekong River source region; SWRS: Salween River source region; YZBR: Yarlung Zangbo River basin.

Area	a	b	c	d	e	f	g	h	i	j	k
NWIA	−8.69 ± 0.47	−8.73 ± 0.48	−8.67 ± 0.47	−8.72 ± 0.47	−8.59 ± 0.48	−8.67 ± 0.48	−8.60 ± 0.48	−8.62 ± 0.49	−9.48 ± 0.48	−9.56 ± 0.48	−9.51 ± 0.48
BBN	−2.99 ± 0.35	−3.00 ± 0.35	−3.05 ± 0.35	−2.99 ± 0.35	−3.10 ± 0.33	−3.09 ± 0.33	−3.15 ± 0.33	−3.07 ± 0.33	−2.93 ± 0.37	−2.93 ± 0.37	−2.98 ± 0.37
TRM	−1.66 ± 0.73	−1.71 ± 0.74	−1.65 ± 0.73	−1.77 ± 0.74	−2.22 ± 0.70	−2.27 ± 0.69	−2.22 ± 0.70	−2.32 ± 0.70	−1.92 ± 0.69	−1.92 ± 0.71	−1.93 ± 0.69
QDM	2.00 ± 0.23	1.97 ± 0.21	1.99 ± 0.22	1.97 ± 0.22	2.08 ± 0.25	2.05 ± 0.24	2.07 ± 0.24	2.05 ± 0.24	1.85 ± 0.25	1.82 ± 0.22	1.84 ± 0.25
ENDR	0.85 ± 0.45	0.64 ± 0.46	0.86 ± 0.45	0.68 ± 0.46	0.62 ± 0.42	0.44 ± 0.43	0.63 ± 0.42	0.49 ± 0.42	1.77 ± 0.40	1.60 ± 0.40	1.76 ± 0.39
YLRS	0.66 ± 0.12	0.77 ± 0.13	0.65 ± 0.12	0.74 ± 0.12	0.77 ± 0.12	0.88 ± 0.12	0.75 ± 0.12	0.85 ± 0.13	0.77 ± 0.13	0.87 ± 0.14	0.76 ± 0.13
YZRS	1.37 ± 0.12	1.38 ± 0.11	1.39 ± 0.12	1.37 ± 0.11	1.30 ± 0.11	1.31 ± 0.11	1.31 ± 0.11	1.30 ± 0.11	1.06 ± 0.10	1.06 ± 0.10	1.07 ± 0.10
MKRS	0.17 ± 0.07	0.20 ± 0.08	0.16 ± 0.08	0.22 ± 0.07	0.19 ± 0.07	0.23 ± 0.07	0.19 ± 0.07	0.24 ± 0.08	0.13 ± 0.06	0.16 ± 0.06	0.12 ± 0.06
SWRS	−0.83 ± 0.12	−0.84 ± 0.13	−0.83 ± 0.12	−0.84 ± 0.12	−0.86 ± 0.11	−0.87 ± 0.12	−0.86 ± 0.11	−0.87 ± 0.12	−1.01 ± 0.11	−1.02 ± 0.12	−1.02 ± 0.10
YZBR	−4.03 ± 0.21	−4.01 ± 0.21	−4.08 ± 0.21	−3.98 ± 0.22	−3.99 ± 0.21	−3.98 ± 0.21	−4.03 ± 0.21	−3.95 ± 0.21	−3.95 ± 0.22	−3.93 ± 0.21	−4.00 ± 0.22
Area	l	m	n	o	p	q	r	s	t	AVE
NWIA	−9.50 ± 0.48	−8.74 ± 0.47	−8.85 ± 0.47	−8.73 ± 0.47	−8.84 ± 0.47	−8.61 ± 0.47	−8.72 ± 0.47	−8.61 ± 0.47	−8.70 ± 0.47	−8.86 ± 0.82
BBN	−2.91 ± 0.37	−3.00 ± 0.36	−3.01 ± 0.36	−3.06 ± 0.35	−3.00 ± 0.36	−3.15 ± 0.34	−3.16 ± 0.35	−3.20 ± 0.34	−3.15 ± 0.34	−3.05 ± 0.38
TRM	−2.00 ± 0.71	−1.65 ± 0.80	−1.69 ± 0.82	−1.66 ± 0.81	−1.75 ± 0.81	−2.21 ± 0.77	−2.23 ± 0.76	−2.22 ± 0.77	−2.29 ± 0.78	−1.96 ± 0.89
QDM	1.82 ± 0.23	2.04 ± 0.20	1.99 ± 0.18	2.01 ± 0.19	1.97 ± 0.19	2.12 ± 0.21	2.08 ± 0.20	2.09 ± 0.21	2.06 ± 0.20	1.99 ± 0.29
ENDR	1.67 ± 0.39	0.91 ± 0.38	0.71 ± 0.40	0.91 ± 0.39	0.74 ± 0.39	0.69 ± 0.36	0.51 ± 0.36	0.69 ± 0.35	0.56 ± 0.36	0.89 ± 0.94
YLRS	0.84 ± 0.14	0.68 ± 0.13	0.81 ± 0.13	0.67 ± 0.13	0.78 ± 0.12	0.80 ± 0.13	0.93 ± 0.13	0.79 ± 0.13	0.90 ± 0.13	0.78 ± 0.20
YZRS	1.05 ± 0.10	1.47 ± 0.10	1.48 ± 0.09	1.52 ± 0.10	1.48 ± 0.10	1.41 ± 0.09	1.41 ± 0.09	1.45 ± 0.09	1.41 ± 0.09	1.33 ± 0.31
MKRS	0.18 ± 0.06	0.21 ± 0.06	0.22 ± 0.06	0.21 ± 0.07	0.24 ± 0.06	0.22 ± 0.06	0.22 ± 0.06	0.22 ± 0.06	0.24 ± 0.06	0.20 ± 0.09
SWRS	−1.02 ± 0.11	−0.86 ± 0.09	−0.88 ± 0.10	−0.86 ± 0.09	−0.88 ± 0.09	−0.87 ± 0.09	−0.89 ± 0.09	−0.87 ± 0.09	−0.89 ± 0.09	−0.89 ± 0.16
YZBR	−3.90 ± 0.22	−4.12 ± 0.21	−4.07 ± 0.22	−4.17 ± 0.21	−4.04 ± 0.21	−4.06 ± 0.20	−4.03 ± 0.21	−4.10 ± 0.20	−4.00 ± 0.21	−4.02 ± 0.24

and Figure A3 and Figure A4. Since the results of the 20 different cases were similar to each other, they reflected the TWS changes at each mascon level very well. This allowed us to use the average results (AVE in Table 1 and Table 2) from mascon inverted solutions as new and improved estimates of monthly and secular mass changes in the TP and its surroundings.

Mainly declining mass-change trends were found for the glacier areas from 2002 to 2021 (Table 1). The largest decrease, of −4.92 ± 1.38 Gt a⁻¹, in a glacier mascon was found in East Nyainqentanglha. The mountains in the Himalayas and Tien Shan also suffered from severe glacier melting of −6.50 ± 1.81 Gt a⁻¹ and −4.91 ± 0.86 Gt a⁻¹, respectively. Pamir–Karakoram–Hindukush showed a weaker rate of glacier melting, of −0.66 ± 1.14 Gt a⁻¹, although there was a notable negative trend in the Pamir region (Figure 2 and Figure 3), which was almost balanced by the obvious positive mass changes in the Hindukush and Karakoram. In addition, small mass increases were also found in the West Kunlun Mountains, whose positive mass balance was suggested in previous papers [2,42,48]. There was also a very weak positive signal in the Qilian region, but with rather large uncertainty given the signal strength. A total decline of −16.26 ± 2.70 Gt a⁻¹ was found in the High Mountain Asia glaciers without glaciers in the inner TP.

Figure 6 shows the glacier-mass changes in each of the 14 mascons over time. For a seasonal comparison with precipitation, snowfall, and temperature, we averaged the results for each month of the year, as shown in Figure 7. We found that the glaciers along the Himalayas (mascons 2 to 5) melted steadily and strongly in the last two decades, except for a relatively small mass-loss trend (but with greater uncertainty) in mascon 5, in the Northwest Himalayas.

For eastern Nyainqentanglha, the glacier-mass change mainly followed the snowfall, and the rainfall in summer had little effect (Figure 6a and Figure 7a). Although the rainfall increased in summer, the glacier mass decreased. The glacier mass therefore showed strong seasonality in this case.

The four regions of mascons 6 (Karakoram), 7 (Hindukush), 8 (Pamir), and 13 (West Kunlun) are closely linked (Figure 1) and directly under the control of, or strongly affected by westerlies [2]. They bring sufficient snowfall to these regions. Hence, the glaciers there show mass increases during periods of rich snowfall and air temperatures below 0 $°\mathrm{C}$ in the winter and spring months, as well as mass decreases during periods of reduced snowfall and high air temperatures (Figure 6f–h,m and Figure 7f–h,m). For Karakoram and West Kunlun, air temperatures below zero and snowfall caused glacier increases before summer. The low monthly temperature average in the winter months (Karakoram, −18.82 $°\mathrm{C}$; West Kunlun, −15.70 $°\mathrm{C}$) and summer months (Karakoram, 3.13 $°\mathrm{C}$; West Kunlun, 4.95 $°\mathrm{C}$), as well as in all months (Karakoram, −7.98 $°\mathrm{C}$; West Kunlun, −5.14 $°\mathrm{C}$) (Figure A5), provided very good conditions for the accumulation of glacier mass, which is the key factor in the formation of the eye-catching ‘Karakoram Anomaly’ and the positive mass balance in West Kunlun [42,48]. However, for Hindukush and Pamir, the air temperature rises above 0 $°\mathrm{C}$ in April, much earlier than in Karakoram and West Kunlun, and the average temperature in summer is also much higher.

The Tien Shan region is divided into four glacier mascons: central part (mascon 9), western part (mascon 10), eastern part (mascon 11), and northern part (mascon 12). Under the influence of westerlies, these four parts have similar glacier-mass-change patterns to Hindukush, Karakoram, Pamir, and West Kunlun. We found that the glacier mass increased when snow fell and the temperature was below zero, and that it decreased when the snowfall ceased and the temperature rose above zero (Figure 6i–l and Figure 7i–l), although these parts did not show positive secular trends like Karakoram and West Kunlun. At mascon 14 (Qilian Shan), the glacier mass underwent frequent changes of small magnitude, with no obvious cyclical effects related to snowfall or precipitation (Figure 6n and Figure 7n).

To further investigate the relationship between the TWS changes and the changes in the climate factors, we calculated the PCCs (see

Table A2. PCCs between seasonal-averaged glacier anomalies/seasonal-averaged TWS anomalies and the seasonal-averaged snowfall or net precipitation.

Glacier Mascons	1	2	3	4	5	6	7	8	9	10	11	12	13	14
PCC	0.60	0.83	0.90	0.76	0.75	0.77	0.86	0.87	0.52	0.78	0.45	0.71	0.48	0.06
Water basins	NWIA	BBN	TRM	QDM	ENDR	YLRS	YZRS	MKRS	SWRS	YZBR	-	-	-	-
PCC	0.89	0.91	0.42	−0.04	0.82	0.24	0.60	0.69	0.74	0.77	-	-	-	-

Note: For glacier mascons, PCCs are between seasonal-averaged glacier anomalies and seasonal-averaged snowfall except for mascon 2, 3 and 4 where PCCs are between seasonal-averaged glacier anomalies and net precipitation. For water basins, PCCs are between TWS seasonal-averaged TWS anomalies and seasonal-averaged net precipitation except for TRM where PCCs are between seasonal-averaged TWS anomalies and seasonal-averaged snowfall. The numbers 1–14 in header indicate the 14 mascons, and the abbreviations mark 10 selected water basins as defined in the main text.

) between the season-averaged glacier anomalies and the season-averaged snowfall, with three exceptions, in the East Himalayas (mascons 2 and 3) and West Himalayas (mascon 4), because they were strongly influenced by net precipitation rather than snowfall (Figure 6b–d and Figure 7b–d). We found that the PCCs were generally larger than 0.5, showing a strong correlation between glacier melting and relevant climatic factors. An exception was Qilian Shan (mascon 14), with a very low correlation. However, its TWS changes were associated with high uncertainty, as stated above.

The water basins surrounding the TP lost water at a significant rate, while most of the water basins in the TP acquired water mass, with two exceptions: SWRS and YZBR (Table 2). The largest decrease, of −8.86 ± 0.82 Gt a⁻¹, was observed in NW India (NWIA), followed by −3.05 ± 0.38 Gt a⁻¹ in the Bengal basin (BBN) and −1.96 ± 0.89 Gt a⁻¹ in the Tarim basin, surrounding the TP.

Compared with the mass balance in the glacier-mascon regions, the local TWS changes in the water basins in the TP and its surroundings were mainly affected by net precipitation. For NWIA and BBN, which are controlled by Indian monsoon, abundant precipitation in summer was the main source of TWS changes, while the nearly year-round high temperatures above 0 °C; resulted in high levels of evaporation (Figure 8a,b and Figure 9a,b). Therefore, the TWS decreased during non-summer months as the rainfall was insufficient, while temperature was highly conducive to evaporation. In summer, the TWS increased due to the abundant rainfall until autumn, when the rainfall decreased to a level comparable to that of evaporation. The differences between two regions are: (1) that the annual amplitude of the TWS in NW India was about 22.4 mm and, thus, much smaller than that of 74.9 mm in the Bengal basin (Figure 8a,b); and (2) that the beginning of the TWS increase to positive levels in NW India was in late June, with the turning point and the start of the negative levels in August and late September, while these phenomena occurred in late April, July, and late September, respectively, in the Bengal basin (Figure 9a,b). This probably resulted in the continuous water loss in the two regions and a stronger loss trend in NW India than in the Bengal basin. The decreasing TWS trends in these two regions (Table 2; Figure 8a,b) mainly due to excessive groundwater depletion for agricultural irrigation, according to reports [40,41,52].

The Tarim basin (TRM) is a large basin partly encircled by the Tian Shan, Pamir, West Kunlun, and Altun mountains. The TWS is decreased over the long term (Figure 8c). The dry climate and high air temperature in the Tarim basin leads to evaporation that mitigates any positive rainfall effects. The basin’s TWS change is also affected by snowfall (Figure 8c and Figure 9c), as it is surrounded by many mountain glaciers (Figure 1). The TWS increases when snow falls before summer and decreases during summer, when the evaporation is larger than the rainfall.

The water basins in the TP, the Qaidam basin (QDM), and the endorheic region (ENDR) gained water in the last 20 years (Figure 8d,e). While the gain in the Qaidam basin was reported strongly influenced by the increasing precipitation combined with the decreasing evaporation [15,53], an increase in the thickness of the active layer due to permafrost degradation provided more unsaturated zones storing water from the increased precipitation and snow/ice melting, and thus provided more opportunity for their infiltration into the shallow and deep aquifers, which can explain the increase in the TWS [9,15]. The TWS increase in the endorheic region was mainly due to lake volume and groundwater increase driven by the enhanced precipitation [4,9]. Figure 9d,e also show that TWS increased in summer, with relatively high levels of rainfall. In addition, we found a delay of about one month in the TWS-change response to the net precipitation changes in the two basins.

The TWS increased in the Three Rivers source region consisting of YLRS, YZRS, and MKRS, which was in accordance with the results presented by Xiang et al. [9]. The TWS changes showed an increasing trend (Figure 8f–h). Summer rainfall was the main cause of the TWS increase (Figure 8f–h and Figure 9f–h). Lakes are not the main water-storage systems in the Three Rivers source region. The increase in the active layer due to permafrost degradation may be one of the reasons for the TWS increase, but another important reason could be the increase in groundwater here, reported by Xiang et al. [9]. In contrast, the TWS values in SWRS and YZBR showed decreasing trends (Figure 8i,j), while the short-term TWS increases mainly occurred during the summer rain. Water discharge is principally related to river runoff and evaporation. Like the Tarim basin, YZBR contains glaciers in Nyainqentanglha, so the TWS increased slightly before summer when snowfall occurred, but the glaciers then rapidly melted from mid-summer onward, causing significant mass loss despite large amounts of net precipitation (Figure 9j). As in the water basins of Qaidam and the endorheic region in the TP, we also found a delayed response of the TWS to precipitation in the river basins of about one month (Figure 9f–i) in the eastern TP. This confirms the results of previous studies [54,55,56] which discussed the possibility of a theoretically delayed response between TWS and precipitation, whereas the delay time varied from days to months as the situation varied.

We also calculated the PCCs (see Table A2) between the TWS season-average anomalies and season-average net precipitation, except for the Tarim basin (TRM). As stated above, the many glaciers surrounding this basin cause the strong glacier melting effects there. Most of the PCCs were generally larger than 0.6, showing a high correlation between TWS changes and net precipitation. There were two lower correlations of 0.42 for TRM and 0.24 for YLRS. For TRM, the TWS changes were strongly influenced by the glacier changes in Tien Shan and West Kunlun, but they were also affected by precipitation coupled with strong evaporation (Figure 8c and Figure 9c). For YLRS, the TWS changes occurred with weak periodicity and at small amplitudes (Figure 8f), which may have concealed their relation to precipitation. However, in QDM, the precipitation was weakly positive to and sometime balanced with strong evaporation (Figure 8d). The TWS changes may also have been driven by permafrost degradation and surrounding glacier melting, which may partly explain the weak correlation with the net precipitation.

4. Discussion

4.1. Comparison with Previous Studies

In previous studies on TWS changes in the TP area, ICESat and ASTER data were used to estimate the ice-mass balance. We summarize the results of four studies in Table 3. To compare our results with those in previous studies, we calculated the TWS changes for the different observation time spans used in these four studies. Given the lower temporal resolution of the ICESat and ASTER data, we first calculated the annually averaged results based on monthly variation and then performed a linear regression to obtain the inter-annual trends.

Our results on the glacier-mass changes match those from the ICESat and ASTER analyses of most glacier mascons. The exceptions are mascon 5 to 7. Our results for mascon 5 (Spiti Lahaul) show significantly less glacier ablation than those from the ICESat and ASTER analyses at different time spans, which may be partly due to the significant upward load displacement [57] offsetting the effects of the glacier ablation, which cannot be distinguished by GRACE. Another cause may be the effect of the westerlies on the snowfall accumulation in winter. Since it is located in the northwest of the Himalayas, mascon 5 is strongly affected by westerlies. Precipitation (as snowfall) in winter and spring accounts for a large proportion of the annual precipitation, sometimes reaching up to 50% [58], and the winter snowfall is mainly influenced by the westerlies [59]. Unlike those of mascons 2 to 4 (Himalayas other than Spiti Lahaul), the glacier mass of mascon 5 is strongly affected by snowfall and increases in the winter and spring months. In summer, glaciers decrease quickly when the temperature rises above zero and snowfall turns into rainfall, until the late autumn, when snow falls, and the temperature drops below zero again (Figure 7e). For mascon 7 (Hindu Kush), Bajracharya et al. [60], using Landsat data, suggested much slower but more steadily retreating glaciers than in the Himalayas, which is not supported by the results from ICESat and ASTER analyses listed in Table 3. Our results instead match the suggestion of Bajracharya et al. [60].

Regarding mascons 6 and 13, we found anomalous gains in glacier mass in Karakoram and West Kunlun, respectively, while the ICESat and ASTER data provide negative values for Karakoram. However, many previous studies support our results: Gardelle et al. [42,43] identified a slight mass gain or balanced mass budget in glaciers during the first decade of the 21st century in Karakoram; Hewitt [61] showed evidence of glacier expansion in central Karakoram from 1997 to 2001; Bhambri et al. [62] pointed out that the glaciers in Karakoram remained stable or increased slightly from the 1970s; and Scherler et al. [63] found that more than 50% of the observed glaciers in Karakoram were advancing or stable between 2000 and 2008, implying positive mass balance. Investigating the causes, Bashir et al. [64] attributed the Karakoram anomaly to increased humidity, cloud cover, precipitation, and decreased net radiation and near-surface wind speed; Forsythe et al. [65] tried to use the ‘Karakoram vortex’ to explain the Karakoram anomaly; Chao et al. [66] investigated the contribution of Middle East irrigation to the growth of the Karakoram glaciers and found that it increases the amount of evaporated moisture that is transferred to Karakoram, increasing the precipitation there. Nonetheless, in view of the controversy, the actual mass balance of Karakoram glaciers and their causes still require further study.

Some studies investigated larger areas that include Karakoram. Yao et al. [2] reported minor glacial retreat but positive mass balance in Karakorum and West Kunlun; Farinotti et al. [44] also showed that Karakoram glaciers are at least balanced or have slightly positive glacier budgets, and that this anomalous glacier behavior partially extends to nearby West Kunlun and Pamir; Liang et al. [46] even referred to the expression of a ‘Kunlun–Pamir–Karakoram’ anomaly and showed mass increase and positive glacier-elevation changes over the period of 2000–2013. These studies strongly suggest that the positive mass balance of glaciers in Karakoram and West Kunlun occur simultaneously under similar climatic conditions.

Focusing on West Kunlun alone, Yasuda and Furuya [49] used Landsat and SAR images from 1972 to 2014 and identified surge-type glaciers that were widely distributed in West Kunlun. Bao et al. [48] found that the glaciers in West Kunlun gained in mass at a rate of 0.23 ± 0.24 m a⁻¹ (in EWT) from 2003. Muhammad and Tian [50] used ASTER DEM, ICESat, and a differential global positioning system to indicate glacier advances and a positive glacier-mass balance in the Guliya ice cap in West Kunlun. Gardner et al. [47], Wang et al. [51], and Shen et al. [45] also reported a positive mass balance in West Kunlun.

For mascons 9 to 12 (Tien Shan), Kääb et al. [67] provided a value of −5.33 ± 4.36 Gt a⁻¹ from 2003 to 2008 based on ICESat data, while our result of −9.64 ± 1.86 Gt a⁻¹ is much larger. On another note, our results match other results based on both ICESat [47,51] and ASTER data [7] over different time spans in Tien Shan, which suggests more confidence in our estimate.

Our results for the TWS trends in the water basins also matched those of previous studies. The TWS-trend rates for ENDR and YZBR from 2003 to 2017 were 0.44 ± 1.14 mm a⁻¹ and −18.80 ± 1.12 mm a⁻¹, respectively, which support the values of 2.15 mm a⁻¹ and −13.18 mm a⁻¹, respectively, reported by Jia et al. [68]. The magnitude for YZBR was slightly larger in this study because the basin boundary of YZBR in our study was slightly larger than that in the study by Jia et al. [68]. Our calculated trend from 2005 to 2013 for ENDR was 5.00 ± 1.59 mm a⁻¹, which is close to the result of 6.199 ± 0.813 mm a⁻¹ obtained by Qiao et al. [69] and matches well within the uncertainties. Similarly, our result for the Qaidam basin from 2003 to 2012 was 2.73 ± 0.21 Gt a⁻¹, which is very close to the 2.24 ± 0.28 Gt a⁻¹ reported by Jiao et al. [15]. In turn, our results for YZRS, YLRS, and YZBR from 2003 to 2014 were 12.36 ± 0.93 mm a⁻¹, 7.38 ± 1.69 mm a⁻¹, and −17.28 ± 1.63 mm a⁻¹, respectively, at least twice as large as the 5.95 mm a⁻¹, 3.78 mm a⁻¹, and −7.59 mm a⁻¹, respectively, reported by Meng et al. [70]. We can only speculate about the reasons for this large difference, but we can note that our results (Figure 2 and Figure 3) match the results of the precipitation trends from the meteorological stations and the China Meteorological Administration and net precipitation (P-E) trends better than those of Meng et al. [70] (see their Figures 7 and 9), which gives more support to our results.

For High Mountain Asia (HMA), including the TP and the Tien Shan region, Chen et al. [71] reported a trend of $-5.6 \pm 4.2$ Gt a⁻¹ from 2002 to 2019, which is much smaller than our trend of $-15.74 \pm 2.92$ Gt a⁻¹. However, our result is very close to −15.6 Gt a⁻¹, which is a sum of the TWS decrease of −10.2 Gt a⁻¹ during the period of 2002–2017 in the TP reported by Li et al. [72] and the glacier-melting trend of −5.4 ± 2.5 Gt a⁻¹ from 2003 to 2019 in Tien Shan reported by Wang et al. [51]. Our result is also supported by Wang et al. [73], who reported −9.55 Gt a⁻¹ in the TP during the period of 2002–2017. If we follow Beveridge et al. [74] and divide the HMA into just four regions, i.e., the Himalayas, Pamir, Qilian, and Tien Shan, to estimate the mass balance of glaciers (see their Figure 1) from April 2002 to May 2016, our results are −17.13 ± 2.29 Gt a⁻¹, −0.74 ± 1.16 Gt a⁻¹, 4.66 ± 1.08 Gt a⁻¹, and −5.69 ± 0.86 Gt a⁻¹, respectively. Beveridge et al. [74] reported −11 ± 3 Gt a⁻¹ for the Himalayas, −0.57 ± 2 Gt a⁻¹ for Pamir, 7.9 ± 2 Gt a⁻¹ for Qilian, and −6.4 ± 1 Gt a⁻¹ for Tien Shan. The results for Pamir and Tien Shan were similar because glaciers are widely distributed in these two regions, which do not have water basins, and the mass changes mainly take the form of glacier melting. In turn, we speculate that the differences between the results for the Himalayas and for Qilian might have been due to the mixed mass changes from the water basin and glacier melting in a mascon, whose performance characteristics are not especially consistent. If we follow Wang et al. [75] and divide the TP into two parts, north and south, the northern part includes QDM, YLRS, YZRS, the northern half of ENDR, the Qilian mascon, and the West Kunlun mascon, while the southern part includes MKRS, SWRS, YZBR, Nyainqentanglha, and the Himalayas, without Spiti Lahaul (mascon 5). Wang et al. [75] reported a positive TWS-change trend of 2.59 mm a⁻¹ (4.20 Gt a⁻¹) for the northern part and a negative trend of −8.65 mm a⁻¹ (−11.73 Gt a⁻¹) for the south, for a total trend of −2.76 mm a⁻¹ (−8.22 Gt a⁻¹) from 2004 to 2015, in the TP. This pattern of slight increase in the north along with a strong decrease in TWS changes in the south supports our results, shown in Section 3, albeit with slightly different values. Our corresponding results were 5.64 Gt a⁻¹, −16.66 Gt a⁻¹, and −11.01 Gt a⁻¹, respectively, which are slightly stronger trends. However, our trend result for the TP was closer to the trend of −10.2 Gt a⁻¹ during the 2002–2017 period reported by Li et al. [72].

Surrounding the TP, our results for the TWS trends for TRM, NWIA, and BBN are consistent with those of previous studies. Our TWS trend of −1.40 ± 0.74 mm a⁻¹ for TRM from 2002 to 2015 matches the −1.4069 ± 0.5060 mm a⁻¹ reported by Zhao and Li [76], and it is very close to the −1.6 ± 1.1 mm a⁻¹ described by Yang et al. [77]. Similarly, for NWIA, considering the soil moisture (SM) increase of 0.36 ± 0.70 Gt a⁻¹ (0.82 ± 1.59 mm a⁻¹), our calculated TWS trend from 2005 to 2010 of −12.2 ± 1.81 Gt a⁻¹ (−27.73 ± 4.11 mm a⁻¹) is close to the groundwater depletion rate of −14 ± 0.4 Gt a⁻¹ (−31 ± 1 mm a⁻¹) presented by Long et al. [41], and also conforms very well to the groundwater-depletion rate of ~16 mm a⁻¹ from 2003 to 2015 reported by Vissa et al. [78] (our results were: TWS, −13.75 ± 2.39 mm a⁻¹; SM, 2.48 ± 0.50 mm a⁻¹). Our TWS trend for BBN from 2003 to 2007 is −6.02 ± 3.90 Gt a⁻¹, which is more than twice that of −2.83 ± 0.42 Gt a⁻¹ given by Shamsudduha et al. [52]. However, the area of BBN we used is twice the size of that used by Shamsudduha et al. [52].

Table 3. Comparison between yearly glacier-mass-change rates in glacier mascons in this study and in previous studies.

Mascon	Glacier Mass Change Trend Rates (Gt a−1)
	ICESat		ASTER	ICESat	GRACE
	2003–2008	2003–2009	2000–2016	2003–2019	2003–2008	2003–2009	2002–2016	2003–2019
1	−8.1 ± 1.9	−4.5 ± 3.3	−4.9 ± 1.8	−7.1 ± 1.4	−6.63 ± 3.60	−7.11 ± 2.54	−5.45 ± 0.76	−5.47 ± 0.64
2	−3.1 ± 0.8	−5.5 ± 1.6	−1.2 ± 0.6	−2.4 ± 0.5	−2.39 ± 1.06	−6.47 ± 1.18	−2.34 ± 0.30	−2.03 ± 0.28
3	−3.1 ± 1.0		−1.9 ± 1.2	−3.0 ± 1.0	−3.55 ± 1.04		−2.79 ± 0.34	−2.57 ± 0.24
4	−3.2 ± 1.1	−3.1 ± 1.8	−1.9 ± 0.5	−3.0 ± 1.0	−1.59 ± 1.44	−1.91 ± 1.06	−1.84 ± 0.36	−1.92 ± 0.34
5	−4.6 ± 1.6	−4.4 ± 1.6	−2.9 ± 0.7	−3.8 ± 1.4	−0.59 ± 2.70	−0.63 ± 1.84	−0.43 ± 0.60	−0.03 ± 0.38
6	−2.1 ± 2.2	−2.6 ± 4.4	−0.7 ± 1.5	−3.0 ± 3.9	1.71 ± 4.28	1.82 ± 4.24	1.39 ± 0.76	1.17 ± 0.52
7	−2.7 ± 1.7		−1.2 ± 0.7	−2.0 ± 1.8	−0.41 ± 4.42		0.15 ± 0.70	0.05 ± 0.50
8	−3.1 ± 2.3	−2.1 ± 4.1	−0.7 ± 0.7	−1.9 ± 1.7	−3.48 ± 4.70	−3.22 ± 3.24	−1.60 ± 0.96	−1.72 ± 0.74
9 + 10 + 11 + 12	−5.33 ± 4.36	−7.5 ± 3.4	−4.0 ± 2.9	−5.4 ± 2.5	−9.64 ± 1.86	−8.54 ± 1.74	−5.27 ± 0.84	−4.57 ± 0.78
13	0.6 ± 1.4	1.5 ± 1.7	1.6 ± 0.9	1.6 ± 2.1	0.57 ± 1.14	0.50 ± 0.78	0.84 ± 0.24	0.74 ± 0.16
14		−0.6 ± 0.8				−0.16 ± 0.17
Source	* Kääb et al. [67]	Gardner et al. [47]	* Brun et al. [7]	Wang et al. [51]	This study

Note: the table values in columns marked with * also refer to Table S2 in the Supporting Information of Wang et al.’s study [51]. Larger differences in previous results are underlined.

Table 3. Comparison between yearly glacier-mass-change rates in glacier mascons in this study and in previous studies.

Mascon	Glacier Mass Change Trend Rates (Gt a−1)
	ICESat		ASTER	ICESat	GRACE
	2003–2008	2003–2009	2000–2016	2003–2019	2003–2008	2003–2009	2002–2016	2003–2019
1	−8.1 ± 1.9	−4.5 ± 3.3	−4.9 ± 1.8	−7.1 ± 1.4	−6.63 ± 3.60	−7.11 ± 2.54	−5.45 ± 0.76	−5.47 ± 0.64
2	−3.1 ± 0.8	−5.5 ± 1.6	−1.2 ± 0.6	−2.4 ± 0.5	−2.39 ± 1.06	−6.47 ± 1.18	−2.34 ± 0.30	−2.03 ± 0.28
3	−3.1 ± 1.0		−1.9 ± 1.2	−3.0 ± 1.0	−3.55 ± 1.04		−2.79 ± 0.34	−2.57 ± 0.24
4	−3.2 ± 1.1	−3.1 ± 1.8	−1.9 ± 0.5	−3.0 ± 1.0	−1.59 ± 1.44	−1.91 ± 1.06	−1.84 ± 0.36	−1.92 ± 0.34
5	−4.6 ± 1.6	−4.4 ± 1.6	−2.9 ± 0.7	−3.8 ± 1.4	−0.59 ± 2.70	−0.63 ± 1.84	−0.43 ± 0.60	−0.03 ± 0.38
6	−2.1 ± 2.2	−2.6 ± 4.4	−0.7 ± 1.5	−3.0 ± 3.9	1.71 ± 4.28	1.82 ± 4.24	1.39 ± 0.76	1.17 ± 0.52
7	−2.7 ± 1.7		−1.2 ± 0.7	−2.0 ± 1.8	−0.41 ± 4.42		0.15 ± 0.70	0.05 ± 0.50
8	−3.1 ± 2.3	−2.1 ± 4.1	−0.7 ± 0.7	−1.9 ± 1.7	−3.48 ± 4.70	−3.22 ± 3.24	−1.60 ± 0.96	−1.72 ± 0.74
9 + 10 + 11 + 12	−5.33 ± 4.36	−7.5 ± 3.4	−4.0 ± 2.9	−5.4 ± 2.5	−9.64 ± 1.86	−8.54 ± 1.74	−5.27 ± 0.84	−4.57 ± 0.78
13	0.6 ± 1.4	1.5 ± 1.7	1.6 ± 0.9	1.6 ± 2.1	0.57 ± 1.14	0.50 ± 0.78	0.84 ± 0.24	0.74 ± 0.16
14		−0.6 ± 0.8				−0.16 ± 0.17
Source	* Kääb et al. [67]	Gardner et al. [47]	* Brun et al. [7]	Wang et al. [51]	This study

Note: the table values in columns marked with * also refer to Table S2 in the Supporting Information of Wang et al.’s study [51]. Larger differences in previous results are underlined.

4.2. Other Factors Introducing Uncertainty

The GIA process represents the ongoing response of the solid Earth to Late Pleistocene deglaciation. Global GIA models usually describe this process accurately, with GIA predominant in the geodetic observations, like North America and Scandinavia, while the TP is far from these regions. Both the GIA and any rebound effects from the Little Ice Age (LIA) in the TP are controversial and very uncertain. Thus, they are not considered here.

The uplift of the TP is mostly cancelled out by the denudation in its periphery [35], while the broad-scale tectonic uplift in High Mountain Asia is isostatically compensated by increasing mass deficiency at depth [79]. Hence, they are not considered in this study.

For the accurate estimation of the glacier-mass balance, we carefully identified the glacier distribution and designed 14 glacier mascons by considering the location and extent of glaciers in previous studies [39,47,67]. Given that the glaciers are distributed on the alpine mountains, where monitoring is scarce and hydrological model results are highly uncertain, we omitted soil moisture from the GLDAS. This may also have introduced errors into the estimates, but we included this effect in our uncertainties.

Another factor is the resolution of satellite gravity. Higher d/o numbers (such as 90 or 120) mean better resolution but cause more errors. We adopted a commonly accepted compromise [14] and used GRACE/GRACE-FO SH solutions up to d/o 60.

5. Conclusions

We determined basin-scale terrestrial water storage (TWS) changes in the Tibetan Plateau and its surroundings from April 2002 to December 2021. We therefore employed three destriping filters (i.e., Duan P4M8, S&W P2M8, and S&W P3M8) together with the latest ITSG and CSR solutions of the Gravity Recovery and Climate Experiment (GRACE) and its follow-on (GRACE-FO) satellite mission, which were recommended in an earlier study. The missing epochs between the GRACE and the GRACE-FO were filled using a singular spectrum analysis. The regularized iterative algorithm and Tikhonov regularization methods were used with the spectral domain inverse method and the space domain inverse method to properly determine the secular and monthly changes for 14 glacier areas and 10 water basins.

The largest mass loss found was that in the glaciers in the Nyainqentanglha mountains and the Eastern Himalayas, with rates of −4.92 ± 1.38 Gt a⁻¹ and −4.34 ± 1.48 Gt a⁻¹, respectively. Tien Shan showed spatial differences in its glacier variations, with the eastern and central parts exhibiting strong negative glacier-mass balance. Although most of the glaciers in the TP showed mass loss, we found small glacier-mass gains of 1.18 ± 0.48 and 0.65 ± 0.21 Gt a⁻¹ in Karakoram and West Kunlun, respectively. We also found nearly balanced glacier-mass changes in Hindukush and Qilian. These glacier changes can be explained by changes in precipitation (especially snowfall).

The TWS changes in the water basins showed that the basins surrounding the TP lost water. The highest water-loss rate, of −8.86 ± 0.82 Gt a⁻¹, occurred in Northwest India, which is in line with previous studies. A rate of −3.05 ± 0.38 Gt a⁻¹ was found in the Bengal basin, and a rate of −1.96 ± 0.89 Gt a⁻¹ was found in the Tarim basin, while most of the water basins in the TP acquired water mass. The endorheic region and the Qaidam basin showed TWS gains at rates of 0.89 ± 0.94 Gt a⁻¹ and 1.99 ± 0.29 Gt a⁻¹, respectively, and the Three Rivers source region also showed obvious increases in TWS changes of 2.31 ± 0.38 Gt a⁻¹. However, the Salween River source region and the Yarlung Zangbo River basin showed decreasing trends. These TWS changes were closely related to precipitation and the melting of ice/snow in and around the basins.