1. Introduction
The panoramic image services provided by Google cover all seven continents, with images of areas inhabited by 98% of the world’s population [
1,
2]. Panoramic images have a wider perspective than typical perspective images, contain more comprehensive buildings and a stronger sense of reality, and have richer scene details [
3]. Owing to the abundant resources and wide field of view (FOV), panoramic images have considerable advantages over perspective images in large-scale, three-dimensional (3D) scene reconstruction [
4,
5]. Three-dimensional scene reconstruction [
6,
7,
8,
9] has been comprehensively studied and applied to digital cities, virtual reality [
10], and SLAM [
11,
12] because of its significant advantages in terms of model accuracy, realism, and ease of modeling. The key problem that needs to be solved to achieve 3D scene reconstruction is image matching [
13,
14,
15]. Image matching is a core technology in digital photogrammetry [
16] and computer vision and is mainly divided into two parts: feature extraction and feature matching. Only when robust and accurate image matching results are obtained can more complex work be performed with good results and continued in-depth research.
Owing to the characteristics of panoramic images, there are problems with image matching. As shown in
Figure 1, most high-resolution panoramic images are obtained using combined lens cameras for various reasons, such as the imaging mechanism and perspective, resulting in significant nonlinear aberrations in different directions of the panoramic image [
17]. This aberration is equivalent to adding a geometric transformation to a perspective image and increases with the distance from the center of the image. To solve the problem of panoramic image matching, numerous experiments have been performed. Most of the current panoramic image matching algorithms still rely on SIFT [
18] because of its invariance to rotation, scale scaling, and grayscale changes. Therefore, the SIFT algorithm is robust for panoramic images with nonlinear distortions. However, the SIFT algorithm takes a lot of time to compute because of the scale space constructed. Additionally, the SURF [
19] algorithm is an improvement on the SIFT algorithm, which greatly improves the computation speed of the SIFT algorithm and is more suitable for panoramic images with large amounts of data. The ORB [
20] algorithm is faster than both the SIFT and ORB algorithms, but it is not rotation-invariant or scale-invariant because it is actually improved on the basis of the BRIEF [
21] algorithm. The ASIFT [
22] algorithm is improved on the basis of the SIFT algorithm. It is a fully affine-invariant algorithm, and SIFT only defines four parameters, while ASIFT defines six parameters, which is better for the adaptation of panoramic images. Most of these algorithms use distance-based methods, such as FLANN [
23], for feature matching. However, the existence of obvious nonlinear distortion in a panoramic image leads to unsatisfactory results for distance-based matching methods between features. The CSIFT [
24] algorithm, on the other hand, proposes SIFT-like descriptors while using kernel line constraints to improve the matching effect. These algorithms still apply the feature extraction and matching algorithms of perspective images directly or in an improved way to panoramic images and cannot adapt to the obvious nonlinear distortion of panoramic images.
In recent years, with the advancement of artificial intelligence, the convolutional neural network (CNN) [
25,
26], based on deep learning [
27,
28], has developed rapidly in the field of computer vision. For image feature extraction and matching, algorithms such as LIFT [
29], SuperPoint [
30], DELF [
31], and D2-Net [
32] have been proposed. With regard to feature extraction, the SP algorithm has the advantages of extracting a large number of features and fast computation and is widely used. With regard to feature matching, the traditional FLANN algorithm only considers the distance between features. The SuperGlue matching algorithm [
33] surpasses the traditional FLANN algorithm by introducing an attentional graph neural network mechanism for both feature matching and mismatch rejection.
The Traditional Cube Projection Model [
34] reprojects the panoramic image into six faces, but there is only one line connecting each face, resulting in poor continuity of the cube model, and each face corresponds to another for matching, and some faces may have a poor overlap rate and an unsatisfactory matching effect.
In this study, the deep learning method was applied to panoramic image matching, and the panoramic image obtained was used for experimental research. We present a practical approach for increasing the speed of deep feature extraction and matching and the number of features extracted through correction and sharing using the Improved Cube Projection Model. Our research provides a new perspective for panoramic image matching. The primary contributions of this study are summarized as follows:
- (1)
The CNN is introduced to the field of panoramic image matching. We aimed to solve the problems of traditional algorithms, which do not have a strong generalization ability and have unsatisfactory applicability to panoramic images. Good results were obtained by matching the images using a CNN.
- (2)
The Traditional Cube Projection Model was improved. To eliminate the characteristics of the discontinuity of the image in each split-frame image of the Traditional Cube Projection Model, the model was extended. Correction of the panoramic image distortion and accelerated matching were achieved using the Improved Cube Projection Model.
- (3)
We propose a dense matching algorithm for panoramic images. It can accurately and efficiently achieve matching between such images, solving the challenge of matching panoramas with significant distortions.
The remainder of the paper is organized as follows:
Section 2 presents the main process and principles of the proposed algorithm.
Section 3 presents multiple sets of experiments, along with an analysis of the experimental results. Finally,
Section 4 describes the limitations of the proposed algorithm and concludes the paper.
2. Principles and Method
2.1. Solution Framework
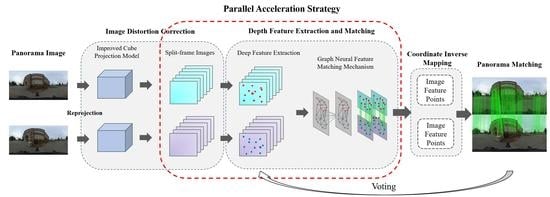
Considering the problems of the nonlinear distortion of panoramic images and the considerable time consumption of deep learning methods, the panoramic images are first mapped to virtual panoramic spheres [
35] through the Equirectangular Projection Model. Then, the Improved Cube Projection Model is used to transform the panoramic sphere in different directions and reproject the panoramic image onto the perspective image with slight distortion in six directions (front, back, left, right, top, and bottom) to realize the correction of the panoramic image. The Superpoint (SP) deep feature extraction algorithm is used to extract features from all directions, and the graph neural network Superglue (SG) matching algorithm is used to search and match the extracted features. The best matching-point pairs are output, and the algorithm is accelerated by processing six split-frame images simultaneously. Finally, the matching points on the image in each direction are mapped back to the panoramic image via coordinate inverse mapping. The solution framework of the matching algorithm is shown in
Figure 2.
2.2. Panoramic Projection Model
2.2.1. Equirectangular Projection
The latitude and longitude coordinates on the virtual panoramic sphere are mapped to the vertical and horizontal coordinates on the plane. After the panoramic image has been unfolded into a plane, its width is twice its height, and there is a one-to-one mapping relationship between any point
p on the spherical panoramic image and the corresponding
P point on the flat panoramic image, as shown in
Figure 3.
Formula (1) presents the relationship between the spherical polar coordinates of point
(
,
,
R) and the flat panoramic image pixel coordinates of
p (
x,
y). Formula (2) describes the correspondence between the spherical polar coordinate system and the spherical right-angle coordinate system [
36].
where
R is the radius of the sphere,
W is the length of the plane image,
is the angle between
and
plane, and
is the angle between the
pendant and
.
Through a simple derivation based on Formulas (1) and (2), the relationship between the flat panoramic image pixel coordinates
p(
x,
y) and the spherical panoramic image space coordinate system coordinates
P(
X,
Y,
Z) on the sphere can be obtained as follows:
2.2.2. Improved Cube Projection Model
The Traditional Cube Projection Model [
37] maps the virtual panoramic sphere onto the six surfaces of the externally cut cube to generate six perspective images, as shown in
Figure 4. The virtual panorama sphere is first mapped to the cube surface using the geometric relationship, and then the cube surface is converted into a perspective image through coordinate transformation. Finally, the mapping relationship between the virtual panoramic sphere and the perspective image is established.
The key to finding the virtual panoramic spherical image points corresponding to the cube image points is to determine which surface of the cube each virtual panoramic spherical image point should be mapped to. Formula (4) is the judgment formula.
,
, and
must have values of +1 or −1, and the virtual panoramic spherical image point must be located in the cube image of one of the six sides. For example, if
= +1, the virtual spherical point should be mapped to the positive
Y, which is the right face of the cube [
38].
where
, which means the maximum absolute value of the three coordinates
X,
Y, and
Z.
In the traditional model, the origin of the cube mapping coordinate system is the center of the image, whereas in the improved model, the upper left corner of the image is the origin. The coordinates in this coordinate system are recalculated, and the cube mapping is converted into a perspective image. The standard mapping relationship of the geometric mapping from the spherical panoramic image to the ordinary image is determined.
As shown in
Figure 5, if the length and width of the plane image are
W and
H, respectively, Formula (5) presents the correspondence between the pixel coordinates (
u,
v) and the plane rectangular coordinates (
x,
y) [
39].
Formula (6) presents the correspondence among the spherical panoramic image point coordinates (X,Y,Z), the cube image point coordinates (,,), and the coordinates of each plane pixel (u,v) (using the front example).
When
= +1, the points on the virtual sphere are mapped to the front [
40].
However, the Traditional Cube Projection Model has problems. It is discontinuous between split-frame images. Therefore, after two panoramic images have been reprojected, the split-frame images are matched one-by-one. Some of the split-frame images may not have high overlap rates, and the matching effect may be unsatisfactory, as shown in
Figure 6.
To address this situation, the Traditional Cube Projection Model was extended to increase the overlap rate between the split-frame images after reprojection, which can result in a better matching effect when the split-frame images are matched one-by-one, as shown in
Figure 7a.
As shown in
Figure 7b, following the above idea, the vertical FOV remains unchanged and the horizontal FOV is increased, so that better matching results can be obtained for the split-frame images with low overlap rates and difficult matching.
2.3. Split-Frame Image Feature Extraction Algorithm
The Split-Frame Image Feature Extraction algorithm achieves the simultaneous extraction of features in six split-frame images, each extracted independently using the SP algorithm. The structure of local feature keys and descriptors is shown in
Figure 8. The SP Extract Feature Network algorithm consists of three modules: the Encoder, Interest Point Decoder, and Descriptor Decoder. The Encoder is built from a lightweight fully convolutional network modified by
[
41], which replaces the fully connected layer at the end of the traditional network with a convolutional layer. The main function of the Encoder is to extract features after the dimensionality reduction of the image, reducing the number of subsequent mesh calculations. Through the Encoder, the input image
is encoded as the intermediate tensor
.
The Interest Point Decoder consists mainly of point-by-point convolutional layers, Softmax activation functions, and tensor transformation functions. In the Interest Point Decoder, the main function of the convolutional layer is to transform the intermediate tensor output of the decoder into a feature graph and then use the Softmax activation function to obtain a feature image of . Using the tensor transformation function, the subpixel convolution method is substituted for the traditional upsampling method, which has the advantage of reducing the calculation workload of the model while restoring the resolution of the feature image. The characteristic curve of can be directly flattened to the thermal map tensor of the eigencurve, and each channel vector in the eigencurve corresponds to the thermal value of the 8 × 8 region of the thermal map. Finally, each value of the heat map tensor characterizes the probability magnitude of the pixel as a feature point.
The Descriptor Decoder is used to generate semi-dense descriptor feature maps, first through the convolutional layer output , as semi-dense descriptors (that is, one output for every eight pixels). Semi-dense descriptors can significantly reduce the memory consumption and computational burden while maintaining the operational efficiency. The decoder then double-triple-interpolates the descriptor to achieve pixel-level accuracy, and finally, the dense feature map is obtained via normalization.
Because the SP algorithm uses Homographic Adaption to improve the generalization ability of the network during training, it has good adaptability to rotation, scaling, and certain distortions. It obtains good feature extraction results on six split-frame images.
2.4. Attentional Graph Neural Network Feature Matching
The six split-frame images of the two panoramic images after the SP algorithm has extracted the deep features are matched using the SG algorithm for deep features. The framework of the SG algorithm is shown in
Figure 9.
The SG is a feature matching and outer point culling network, which enhances the features of key points using a GNN and transforms feature matching problems into solutions for differentially optimized transfer problems. The algorithm consists of two main modules: the Attentional Graph Neural Network and the Optimal Matching Layer. The Attentional Graph Neural Network integrates the location information of the feature points with the description subinformation after coding and then interweaves the L wheel through the attention layer and the cross attention layer, aggregating the context information within the image and between the images to obtain a more specific feature matching vector f for matching.
The Optimal Matching Layer calculates the internal product between the feature matching vectors
f using Formula (7) to obtain the matching degree score matrix
, where
M and
N represent the numbers of feature points in images
A and
B, respectively.
where
represents the inner product, and
and
are the feature matching vectors of images
A and
B, respectively, which are output by the feature enhancement module.
Because some feature points are affected by problems such as occlusion and there is no matching point, the algorithm uses the garbage-bin mechanism, as indicated by Formula (8). The garbage bin consists of a new row and column based on the score matrix, which is used to determine whether the feature has a matching point. SuperGlue treats the final matching result as an allocation problem, constructs the optimization problem by calculating the allocation matrix
and the scoring matrix
S, and solves
P by maximizing the overall score
,
,
. The optimal feature assignment matrix
P is quickly and iteratively solved using the Sinkhorn algorithm; thus, the optimal match is obtained.
where
N and
M represent the bins in
A and
B, respectively. The matching number of each bin is identical to the number of key points in the other group.
2.5. Coordinate Inverse Mapping Algorithm
As shown in
Figure 10a, the coordinates of the corresponding
P on the virtual panoramic sphere are calculated using the split-frame image coordinates (
i,
j).
Then, the
P coordinates are used to calculate the corresponding latitude and longitude.
According to the latitude and longitude, the index coordinates of
P (
I,
J) of the panoramic image corresponding to the latitude and longitude are found in the panorama using the Equirectangular Projection Model. Using Formula (11), the coordinates of the feature points of the perspective image can be mapped back to the panoramic image.
In the Improved Cube Projection Model, because we increase the overlap of adjacent split-frame images, split-frame images in multiple directions may match a pair of image points with the same name at the same time. Therefore, we employ a simple voting mechanism [
42] in the process of mapping the binning image coordinates back to the panoramic image.
When multiple coordinates mapped back to the panoramic image are within a certain threshold, these points are considered to be the same image point, and the voting mechanism is triggered. The Euclidean distance between the midpoint of the original split image and the image center point is calculated separately. A shorter distance to the image principal point corresponds to a smaller aberration. Therefore, a shorter distance corresponds to a higher score, and the panoramic coordinate is selected as the final coordinate.
where
is the center of image.
3. Results and Discussion
The details regarding the experimental data are presented in
Table 1. Three types of test data were used: indoor panoramic images, outdoor panoramic images, and underground panoramic images. The resolutions were identical, but the types of images differed, giving very representative data for the test algorithm.
Figure 11 shows thumbnails of the test images. The first group was taken indoors, and the image displacement was small, but the aberration was large. The second group was shot outdoors. The image displacement was larger than that for the first group, and the aberration was slightly smaller than that for the first group. The third group was shot in an underground garage, and some areas were shadowed or poorly lit.
To validate the proposed algorithm, multiple sets of panoramic image data were used to conduct experiments, and the results were compared with those of other algorithms. The deep learning model was implemented using the PyTorch framework. The SP and SG models adopted the official pretraining weight file. The computer used for the test was a Lenovo Y9000K Notebook. The CPU was i7-10875H, and the graphics card was GeForce RTX 2080. The implementation language was Python, the operating system was Ubuntu 20.04 64-bit, and the CUDA Toolkit version was 11.3. Relevant experiments were conducted for all aspects of the proposed framework, and the experimental results were analyzed using different evaluation metrics.
3.1. Distortion Correction Effect
The reprojection of the panoramic image into the split-frame images in six directions is a process similar to perspective transformation.
Figure 12 shows the transformation of the image after reprojection. From the experimental results, it can be seen that the reprojected image satisfies the basic characteristics of the perspective image. The nonlinear distortion of the key buildings is basically eliminated, and the shapes of the key buildings and objects conform to their spatial geometric characteristics, which is convenient for subsequent feature extraction and matching.
3.2. Extension-Angle Test
The Traditional Cube Projection Model was used to perform an experimental verification of the proposed algorithm, and the results are shown in
Figure 13a.
As shown in
Figure 13a, the split-frame images in all directions are discontinuous, which led to difficulty in extracting the building features at the junction. Therefore, we adopted the strategy of model extension to enhance the continuity between the directions. Experimental validation was performed for different extension angles.
As shown in
Figure 13b, the buildings that were not successfully matched before were well matched with the Improved Cube Projection Model, resulting in a more uniform and dense distribution of matching points.
We used the number of correct matching points obtained and the matching time as the main evaluation indexes. We selected extension angles of 5°, 10°, and 15° and then conducted a comparison test. The experimental results are presented in
Table 2, and the experimental effect graph is shown in
Figure 14. A comprehensive analysis indicated that the 10° extension angle achieved better results for image matching than the 5° extension angle at the expense of a lower time efficiency. The 15° extension angle increased the number of matching points slightly compared with the 10° extension angle, but the time efficiency decreased significantly. Therefore, in subsequent experiments, the 10° extension angle was adopted.
3.3. Voting Mechanism Effect
The matching experiments were first performed directly using the Traditional Cube Projection Model after applying the extension angle, and the problem of duplicate matching points appeared in four regions, as shown in
Figure 15. The details are shown in
Figure 16a. There are many duplicate matching points.
As shown in
Figure 16b, the voting mechanism designed in this study solves this problem perfectly. The feature points of the remapped panoramic image are accurate, and no duplicate matching points are generated.
3.4. Adaptability of the Algorithm
As shown in
Figure 17, several other algorithms do not extract features or extract fewer feature points in the region with large indoor distortion. The proposed algorithm extracted uniform and dense feature points in the area with large indoor distortion and performed well.
The red box in
Figure 18 shows an environment with poor lighting conditions, and the other algorithms in the test experiments were unable to extract features in this area. In contrast, the proposed algorithm performed well because of the SP and SG deep learning approach with a strong generalization ability and good adaptability to different environments.
3.5. Feature Matching Number and Precision
The correct matching point was determined as shown in the formula:
where
is the true location of the feature point.
is the actual position of the feature point calculated by the algorithm.
The proposed method was compared with the SIFT, ASIFT, and Improved ASIFT [
43] algorithms using three sets of experimental data, and the experimental results are shown in
Table 3. The experimental results of various algorithms for image feature extraction and matching are shown in
Figure 19.
Table 3 shows that SIFT matching takes the longest amount of time, eight times longer than the ASIFT algorithm and thirty times longer than the improved ASIFT algorithm and the algorithm in this paper. The algorithm in this paper has the highest accuracy with the shortest matching elapsed time. It is 5% higher than the improved ASIFT, 20% higher than the ASIFT algorithm, and 55% higher than the SIFT algorithm.
Figure 19 and
Figure 20 shows that the SIFT algorithm obtained a small number of matching points with an uneven distribution. The ASIFT algorithm obtained the largest number of matching points, but the distribution was not uniform, and the distortion area could not extract enough feature points. The Improved ASIFT algorithm had a more uniform distribution of matching points but a smaller number. Our algorithm extracted more matching points than the Improved ASIFT with a more uniform and reasonable distribution.
4. Conclusions and Discussion
Panoramic image matching is a challenging task. Faced with the interference caused by the large nonlinear distortion of panoramic images, it is difficult to achieve results comparable to those for perspective images using traditional feature extraction and matching algorithms. Therefore, we used the Improved Cube Projection Model for aberration correction to improve the matching effect of panoramic images. The image matching time was reduced via the acceleration strategy of processing split-frame images simultaneously.
We extended the Traditional Cube Projection Model to address the shortcomings of discontinuity among the split-frame images of the Traditional Cube Projection Model. More uniform and robust matching was achieved on the basis of sacrificing time efficiency. Using the SP and SG deep learning approach, the powerful generalization ability of the deep learning network was utilized to maintain good results in cases of large distortions or poor lighting conditions.
We confirmed the feasibility of using CNNs for panoramic image matching and made targeted improvements to address shortcomings in the application process, which yielded good matching results. This study provides new ideas and methods for large-scale 3D scene reconstruction using panoramic images. In this paper, the CNN was used to achieve a good matching effect and was shown to accurately describe the relative position relationship between images and has important potential value in several fields. It provides an accurate viewpoint and position relationship for building digital cities and facilitates the construction of more complete and detailed digital city models. At the same time, it can acquire a large number of image points with the same name in the image, which provides a large number of virtual control points for SLAM and improves its accuracy when building maps.
Although the proposed method in this paper achieved a good performance level, there are still several limitations in our method. Because the proposed algorithm reprojects the panoramic image onto split-frame images in different directions, the corresponding directional split-frame images are matched one-by-one. Therefore, it is not suitable for images with different imaging modes. When composing a panoramic image, one imaging mode is that the image captured by the forward-facing lens is in the center of the panoramic image; the other imaging mode is that the image captured by the forward-facing lens is at the edge of the panoramic image. When the proposed algorithm was tested on such images, the results were unsatisfactory.
The idea of converting panoramic images to perspective images is still used to implement CNNs for panoramic images. In future research, we will explore the idea of using panoramic image datasets directly to train CNN networks to achieve a better matching performance. We will also continue to study other work after matching, so as to play a more important role in digital city or 3D reconstruction.