Water Body Extraction from Sentinel-2 Imagery with Deep Convolutional Networks and Pixelwise Category Transplantation
Abstract
:1. Introduction
- 1.
- Although previous works have studied the performance of FCNs in the task of water body extraction, there were insufficient discussions on the impacts of band selection on model performance. To address this, we evaluated several state-of-the-art FCNs and compared their performances on RGB, NIR, and multispectral features.
- 2.
- Water body extraction based on machine learning is frequently subject to class imbalance in the dataset. This is often due to the category of interest occupying only a small portion of an image. The traditional solution to this problem is to design the loss function to place greater emphasis on the minority class. Thus, we examined a variety of previously proposed loss functions and provided a thorough analysis of their relative performances on our dataset.
- 3.
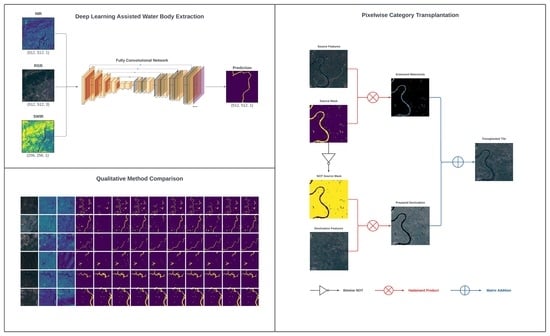
- While FCNs have already demonstrated promising results in water body detection, the training of such models requires access to large quantities of accurately labelled data. Unfortunately, a sizeable database of appropriately labelled images, such as ImageNet [22], is not presently available for remotely sensed data [23]. Furthermore, water is often underrepresented in many datasets due to occupying only a small portion of an image. To address these issues, we introduced PCT, a novel form of data augmentation applicable to both water body extraction and image segmentation in general.
2. Materials and Methods
2.1. Data Source and Preparation
2.1.1. Characteristics and Exploratory Analysis
2.1.2. Data Generation Pipeline
2.2. Methodology
2.2.1. Loss Function
2.2.2. Spectral Contribution in Water Body Detection
2.2.3. Experimental Procedure
2.3. Pixelwise Category Transplantation
3. Results
3.1. Loss Function Evaluation
3.2. Baseline Model Evaluation
3.3. Various Spectral Band Contribution in Water Body Detection
3.4. Pixelwise Category Transplantation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shao, Z.; Fu, H.; Li, D.; Altan, O.; Cheng, T. Remote sensing monitoring of multi-scale watersheds impermeability for urban hydrological evaluation. Remote Sens. Environ. 2019, 232, 111338. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H. A Review on Applications of Remote Sensing and Geographic Information Systems (GIS) in Water Resources and Flood Risk Management. Water 2018, 10, 608. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Zhang, Y.; Ling, X.; Huang, X. Automatic and Unsupervised Water Body Extraction Based on Spectral-Spatial Features Using GF-1 Satellite Imagery. IEEE Geosci. Remote Sens. Lett. 2019, 16, 927–931. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Li, L.; Yan, Z.; Shen, Q.; Cheng, G.; Gao, L.; Zhang, B. Water Body Extraction from Very High Spatial Resolution Remote Sensing Data Based on Fully Convolutional Networks. Remote Sens. 2019, 11, 1162. [Google Scholar] [CrossRef] [Green Version]
- Feng, W.; Sui, H.; Huang, W.; Xu, C.; An, K. Water Body Extraction From Very High-Resolution Remote Sensing Imagery Using Deep U-Net and a Superpixel-Based Conditional Random Field Model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 618–622. [Google Scholar] [CrossRef]
- Miao, Z.; Fu, K.; Sun, H.; Sun, X.; Yan, M. Automatic Water-Body Segmentation From High-Resolution Satellite Images via Deep Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 602–606. [Google Scholar] [CrossRef]
- Yuan, K.; Zhuang, X.; Schaefer, G.; Feng, J.; Guan, L.; Fang, H. Deep-Learning-Based Multispectral Satellite Image Segmentation for Water Body Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7422–7434. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. arXiv 2018. [Google Scholar] [CrossRef] [Green Version]
- Alom, M.Z.; Yakopcic, C.; Taha, T.M.; Asari, V.K. Nuclei Segmentation with Recurrent Residual Convolutional Neural Networks based U-Net (R2U-Net). In Proceedings of the NAECON 2018—IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 23–26 July 2018; pp. 228–233. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-Unet: Unet-like Pure Transformer for Medical Image Segmentation. arXiv 2021, arXiv:2105.05537. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Lin, T.Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 936–944. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation; Springer: Cham, Switzerland, 2018; pp. 833–851. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Xing, M.; Sun, G.C.; Chen, J.; Li, M.; Hu, Y.; Bao, Z. Water Body Detection in High-Resolution SAR Images With Cascaded Fully-Convolutional Network and Variable Focal Loss. IEEE Trans. Geosci. Remote Sens. 2021, 59, 316–332. [Google Scholar] [CrossRef]
- Kang, J.; Guan, H.; Peng, D.; Chen, Z. Multi-scale context extractor network for water-body extraction from high-resolution optical remotely sensed images. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102499. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]
- Schmitt, M.; Ahmadi, S.A.; Hansch, R. There is No Data Like More Data - Current Status of Machine Learning Datasets in Remote Sensing. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 1206–1209. [Google Scholar] [CrossRef]
- Ulamm. Map of Sichuan Basin. 2013. Available online: https://commons.wikimedia.org/w/index.php?curid=30096268" (accessed on 10 December 2013).
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Cardoso, M.J. Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer International Publishing: Cham, Switzerland, 2017; pp. 240–248. [Google Scholar] [CrossRef] [Green Version]
- Salehi, S.S.M.; Erdogmus, D.; Gholipour, A. Tversky Loss Function for Image Segmentation Using 3D Fully Convolutional Deep Networks. In Proceedings of the Machine Learning in Medical Imaging; Springer International Publishing: Cham, Switzerland, 2017; pp. 379–387. [Google Scholar] [CrossRef] [Green Version]
- Abraham, N.; Khan, N.M. A Novel Focal Tversky Loss Function With Improved Attention U-Net for Lesion Segmentation. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 683–687. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]











| Loss Function | Performance (mIoU) | Precision (%) | Recall (%) |
|---|---|---|---|
| Weighted BCE | 62.007 | 30.596 | 92.019 |
| BCE | 73.537 | 77.830 | 57.299 |
| Focal | 73.403 | 76.872 | 57.724 |
| Focal Tversky | 73.900 | 61.504 | 75.802 |
| Tversky | 74.131 | 62.422 | 76.111 |
| Jaccard | 74.509 | 70.218 | 65.538 |
| Dice | 74.943 | 70.809 | 68.818 |
| Dice + BCE | 75.235 | 72.673 | 67.492 |
| Jaccard + BCE | 75.420 | 73.066 | 68.026 |
| Model | RGB (mIoU) | NIR (mIoU) | Multispectral (mIoU) |
|---|---|---|---|
| NDWI [3] | - | - | 3.280 |
| MNDWI [4] | - | - | 10.440 |
| FPN [18] | 63.888 | 69.562 | 71.408 |
| DeepLabV3+ [19] | 65.674 | 71.737 | 72.032 |
| Swin-Unet [16] | 67.726 | 70.675 | 73.264 |
| U-Net [13] | 71.952 | 73.849 | 74.532 |
| U-Net++ [14] | 71.309 | 73.308 | 74.551 |
| Attention U-Net [17] | 71.061 | 72.870 | 74.763 |
| DeepLabV3+ (ImageNet) [19] | 72.955 | 74.791 | 75.403 |
| R2U-Net [15] | 73.267 | 73.570 | 75.420 |
| Model | Baseline (mIoU) | PCT (mIoU) | Best (%) | Gain (mIoU) |
|---|---|---|---|---|
| FPN [18] | 71.408 | 72.130 | 5% | 0.722 |
| DeepLabV3+ [19] | 72.032 | 73.334 | 15% | 1.302 |
| Swin-Unet [16] | 73.264 | 74.267 | 5% | 1.003 |
| Attention U-Net [17] | 74.763 | 75.269 | 5% | 0.506 |
| DeepLabV3+ (ImageNet) [19] | 75.403 | 75.728 | 15% | 0.325 |
| R2U-Net [15] () | 74.828 | 75.657 | 10% | 0.829 |
| U-Net++ [14] | 74.551 | 75.445 | 5% | 0.894 |
| U-Net [13] | 74.532 | 75.546 | 10% | 1.014 |
| R2U-Net [15] () | 75.424 | 75.710 | 10% | 0.286 |
| R2U-Net [15] () | 75.420 | 76.024 | 15% | 0.604 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billson, J.; Islam, M.S.; Sun, X.; Cheng, I. Water Body Extraction from Sentinel-2 Imagery with Deep Convolutional Networks and Pixelwise Category Transplantation. Remote Sens. 2023, 15, 1253. https://doi.org/10.3390/rs15051253
Billson J, Islam MS, Sun X, Cheng I. Water Body Extraction from Sentinel-2 Imagery with Deep Convolutional Networks and Pixelwise Category Transplantation. Remote Sensing. 2023; 15(5):1253. https://doi.org/10.3390/rs15051253
Chicago/Turabian StyleBillson, Joshua, MD Samiul Islam, Xinyao Sun, and Irene Cheng. 2023. "Water Body Extraction from Sentinel-2 Imagery with Deep Convolutional Networks and Pixelwise Category Transplantation" Remote Sensing 15, no. 5: 1253. https://doi.org/10.3390/rs15051253
APA StyleBillson, J., Islam, M. S., Sun, X., & Cheng, I. (2023). Water Body Extraction from Sentinel-2 Imagery with Deep Convolutional Networks and Pixelwise Category Transplantation. Remote Sensing, 15(5), 1253. https://doi.org/10.3390/rs15051253