The Early Identification and Spatio-Temporal Characteristics of Loess Landslides with SENTINEL-1A Datasets: A Case of Dingbian County, China
Abstract
:1. Introduction
2. Study Area
3. Datasets and Methodology
3.1. Datasets
3.2. Methodology
3.2.1. Tropospheric Delay Correction
3.2.2. The Optimization of Interferograms Selection
3.2.3. Evaluation of Landslide Activity
3.2.4. Correlation between Landslide Deformation and Rainfall
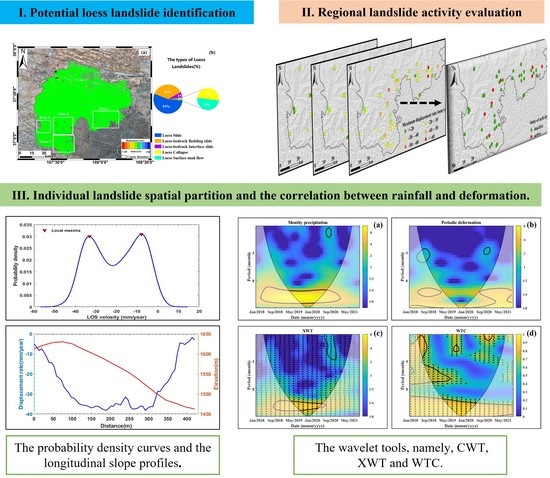
4. Results
4.1. The Identification of Potential Loess Landslides
4.2. Characteristics of the Detected Loess Landslides
4.3. The Activity of Detected Loess Landslides
5. Discussion
5.1. Landslide Spatial Kinematics Analysis
5.2. Landslide Temporal Kinematics Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Method | Individual Interferograms of Dataset from Frame 120 | Individual Interferograms of Dataset from Frame 115 | ||
|---|---|---|---|---|
| Number of Reduced Std | Std Mean [rad] | Number of Reduced Std | Std Mean [rad] | |
| No correction | 748 | 3.524 | 1105 | 2.629 |
| LM | 748 | 2.594 | 1105 | 2.319 |
| LM−DT | 748 | 1.840 | 1105 | 1.500 |
| QT−SP | 748 | 1.245 | 1105 | 1.138 |
Appendix B

Appendix C


References
- Wang, L.; Shao, M.; Wang, Q.; Gale, W.J. Historical changes in the environment of the Chinese Loess Plateau. Environ. Sci. Policy 2006, 9, 675–684. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Wang, G.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in Loess Plateau: A case study in Shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Derbyshire, E. Geological hazards in loess terrain, with particular reference to the loess regions of China. Earth-Sci. Rev. 2001, 54, 231–260. [Google Scholar] [CrossRef]
- Peng, J.; Wang, S.; Wang, Q.; Zhuang, J.; Huang, W.; Zhu, X.; Leng, Y.; Ma, P. Distribution and genetic types of loess landslides in China. J. Asian Earth Sci. 2019, 170, 329–350. [Google Scholar] [CrossRef]
- Duan, Z.; Cheng, W.-C.; Peng, J.-B.; Wang, Q.-Y.; Chen, W. Investigation into the triggering mechanism of loess landslides in the south Jingyang platform, Shaanxi province. Bull. Eng. Geol. Environ. 2018, 78, 4919–4930. [Google Scholar] [CrossRef]
- Li, T.; Wang, C.; Li, P. Loess Deposit and Loess Landslides on the Chinese Loess Plateau. In Progress of Geo-Disaster Mitigation Technology in Asia; Environmental Science and Engineering Book Series; Springer: Berlin/Heidelberg, Germany, 2013; pp. 235–261. [Google Scholar] [CrossRef]
- Shi, X.; Xu, Q.; Zhang, L.; Zhao, K.; Dong, J.; Jiang, H.; Liao, M. Surface displacements of the Heifangtai terrace in Northwest China measured by X and C-band InSAR observations. Eng. Geol. 2019, 259, 105181. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Onn, F.; Zebker, H.A. Correction for interferometric synthetic aperture radar atmospheric phase artifacts using time series of zenith wet delay observations from a GPS network. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Liao, M.; Gong, J. Improved correction of seasonal tropospheric delay in InSAR observations for landslide deformation monitoring. Remote Sens. Environ. 2019, 233, 111370. [Google Scholar] [CrossRef]
- Liao, M.; Jiang, H.; Wang, Y.; Wang, T.; Zhang, L. Improved topographic mapping through high-resolution SAR interferometry with atmospheric effect removal. ISPRS J. Photogramm. Remote Sens. 2013, 80, 72–79. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Q.; Pepe, A.; Mastro, P.; Zhao, C.; Lu, Z.; Zhu, W.; Yang, C.; Zhang, J. Analysis of Groundwater Depletion/Inflation and Freeze–Thaw Cycles in the Northern Urumqi Region with the SBAS Technique and an Adjusted Network of Interferograms. Remote Sensing 2021, 13, 2144. [Google Scholar] [CrossRef]
- Meng, Q.; Xu, Q.; Wang, B.; Li, W.; Peng, Y.; Peng, D.; Qi, X.; Zhou, D. Monitoring the regional deformation of loess landslides on the Heifangtai terrace using the Sentinel-1 time series interferometry technique. Nat. Hazards 2019, 98, 485–505. [Google Scholar] [CrossRef]
- Crippa, C.; Valbuzzi, E.; Frattini, P.; Crosta, G.B.; Spreafico, M.C.; Agliardi, F. Semi-automated regional classification of the style of activity of slow rock-slope deformations using PS InSAR and SqueeSAR velocity data. Landslides 2021, 18, 2445–2463. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.B.; Rossini, M.; Allievi, J. Activity and kinematic behaviour of deep-seated landslides from PS-InSAR displacement rate measurements. Landslides 2018, 15, 1053–1070. [Google Scholar] [CrossRef]
- Meng, Q.; Confuorto, P.; Peng, Y.; Raspini, F.; Bianchini, S.; Han, S.; Liu, H.; Casagli, N. Regional Recognition and Classification of Active Loess Landslides Using Two-Dimensional Deformation Derived from Sentinel-1 Interferometric Radar Data. Remote Sens. 2020, 12, 1541. [Google Scholar] [CrossRef]
- Xu, Y.; Allen, M.B.; Zhang, W.; Li, W.; He, H. Landslide characteristics in the Loess Plateau, northern China. Geomorphology 2020, 359, 107150. [Google Scholar] [CrossRef]
- Li, Y.; Mo, P. A unified landslide classification system for loess slopes: A critical review. Geomorphology 2019, 340, 67–83. [Google Scholar] [CrossRef]
- Liang, J.; Dong, J.; Zhang, S.; Zhao, C.; Liu, B.; Yang, L.; Yan, S.; Ma, X. Discussion on InSAR Identification Effectivity of Potential Landslides and Factors That Influence the Effectivity. Remote Sens. 2022, 14, 1952. [Google Scholar] [CrossRef]
- Kang, Y.; Zhao, C.; Zhang, Q.; Lu, Z.; Li, B. Application of InSAR Techniques to an Analysis of the Guanling Landslide. Remote Sens. 2017, 9, 1046. [Google Scholar] [CrossRef]
- Kang, Y.; Lu, Z.; Zhao, C.; Xu, Y.; Kim, J.-w.; Gallegos, A.J. InSAR monitoring of creeping landslides in mountainous regions: A case study in Eldorado National Forest, California. Remote Sens. Environ. 2021, 258, 112400. [Google Scholar] [CrossRef]
- Pepe, A. Multi-Temporal Small Baseline Interferometric SAR Algorithms: Error Budget and Theoretical Performance. Remote Sens. 2021, 13, 557. [Google Scholar] [CrossRef]
- Tomás, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using wavelet tools to analyse seasonal variations from InSAR time-series data: A case study of the Huangtupo landslide. Landslides 2015, 13, 437–450. [Google Scholar] [CrossRef] [Green Version]
- Ikuemonisan, F.E.; Ozebo, V.C.; Olatinsu, O.B. Investigation of Sentinel-1-derived land subsidence using wavelet tools and triple exponential smoothing algorithm in Lagos, Nigeria. Environ. Earth Sci. 2021, 80, 722. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Tomás, R.; Pastor, J.L.; Béjar-Pizarro, M.; Bonì, R.; Ezquerro, P.; Fernández-Merodo, J.A.; Guardiola-Albert, C.; Herrera, G.; Meisina, C.; Teatini, P.; et al. Wavelet analysis of land subsidence time-series: Madrid Tertiary aquifer case study. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 353–359. [Google Scholar] [CrossRef] [Green Version]
- Bekaert, D.P.S.; Handwerger, A.L.; Agram, P.; Kirschbaum, D.B. InSAR-based detection method for mapping and monitoring slow-moving landslides in remote regions with steep and mountainous terrain: An application to Nepal. Remote Sens. Environ. 2020, 249, 111983. [Google Scholar] [CrossRef]
- Xu, L.; Dai, F.; Tu, X.; Tham, L.G.; Zhou, Y.; Iqbal, J. Landslides in a loess platform, North-West China. Landslides 2013, 11, 993–1005. [Google Scholar] [CrossRef]
- Wang, G.; Li, T.; Xing, X.; Zou, Y. Research on loess flow-slides induced by rainfall in July 2013 in Yan’an, NW China. Environ. Earth Sci. 2014, 73, 7933–7944. [Google Scholar] [CrossRef]
- Zhao, C.; Kang, Y.; Zhang, Q.; Lu, Z.; Li, B. Landslide Identification and Monitoring along the Jinsha River Catchment (Wudongde Reservoir Area), China, Using the InSAR Method. Remote Sens. 2018, 10, 993. [Google Scholar] [CrossRef]
- Li, L.; Lan, H.; Strom, A. Automatic generation of landslide profile for complementing landslide inventory. Geomat. Nat. Hazards Risk 2020, 11, 1000–1030. [Google Scholar] [CrossRef]
- Wang, H.; Sun, P.; Zhang, S.; Han, S.; Li, X.; Wang, T.; Guo, Q.; Xin, P. Rainfall-induced landslide in loess area, Northwest China: A case study of the Changhe landslide on September 14, 2019, in Gansu Province. Landslides 2020, 17, 2145–2160. [Google Scholar] [CrossRef]
- Gu, T.; Wang, J.; Lin, H.; Xue, Q.; Sun, B.; Kong, J.; Sun, J.; Wang, C.; Zhang, F.; Wang, X. The Spatiotemporal Relationship between Landslides and Mechanisms at the Heifangtai Terrace, Northwest China. Water 2021, 13, 3275. [Google Scholar] [CrossRef]















| Parameter | L1 | L2 | L3 | L4 | L5 |
|---|---|---|---|---|---|
| Activity Index | 0.49 | 0.62 | 0.13 | 0.07 | 0.15 |
| Mean deformation rate | −20.4 | −28.9 | −9.7 | −9.1 | −12.1 |
| Maximum deformation rate | 0.03 | 0.03 | 0.00 | 0.02 | 0.03 |
| Minimum deformation rate | 46.9 | 64.5 | 38.8 | 25.2 | 28.1 |
| Median deformation rate | −19.3 | −27.8 | −8.1 | −8.1 | −10.3 |
| 25 percentile of deformation rate | −32.1 | −45.2 | −13.1 | −13.7 | −16.9 |
| 50 percentile of deformation rate | −19.3 | −27.9 | −8.1 | −8.1 | −10.3 |
| 70 percentile of deformation rate | −8.8 | −11.9 | −2.3 | −3.6 | −7.4 |
| Deformation rate standard deviation | 1.3 | 1.6 | 1.0 | 0.9 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Zhao, C.; Yan, M.; Wang, B.; Liu, X. The Early Identification and Spatio-Temporal Characteristics of Loess Landslides with SENTINEL-1A Datasets: A Case of Dingbian County, China. Remote Sens. 2022, 14, 6009. https://doi.org/10.3390/rs14236009
Jiang Z, Zhao C, Yan M, Wang B, Liu X. The Early Identification and Spatio-Temporal Characteristics of Loess Landslides with SENTINEL-1A Datasets: A Case of Dingbian County, China. Remote Sensing. 2022; 14(23):6009. https://doi.org/10.3390/rs14236009
Chicago/Turabian StyleJiang, Zhuo, Chaoying Zhao, Ming Yan, Baohang Wang, and Xiaojie Liu. 2022. "The Early Identification and Spatio-Temporal Characteristics of Loess Landslides with SENTINEL-1A Datasets: A Case of Dingbian County, China" Remote Sensing 14, no. 23: 6009. https://doi.org/10.3390/rs14236009