1. Introduction
Most of the concrete structures in service have various kinds of defects, such as voids, cracks, delamination, and untightness, which are caused by environmental factors, inadequate construction, or poor maintenance. To prevent these defects from jeopardizing the security of concrete structures, it is necessary to conduct routine inspections and assessments. Ground penetrating radar (GPR), a non-destructive testing method, has been extensively used in concrete-structure inspection because of its desirable reliability and effectiveness [
1,
2,
3,
4,
5,
6]. As a near-surface-level geophysical detection technique, GPR deduces the subsurface’s condition by transmitting high-frequency electromagnetic waves into the structure and receiving echoes in which there are electromagnetic property contrasts. Several received echoes form a GPR B-scan image (radargram), and hereafter the technicians deduce the structure of the subsurface medium according to the characteristics of the reflected waveforms. However, the interpretation of GPR data is a challenging task. The obtained GPR data are reflected electromagnetic waveforms of the subsurface, which are difficult to interpret. This makes the experience and expertise of technicians essential to identify targets from GPR images correctly [
7]. Furthermore, when the amount of data is enormous, the interpretation of GPR data becomes a time- and labor-consuming task. Automatic identification methods for GPR data are urgently needed to improve the efficiency and accuracy.
With the emergence of convolutional neural networks (CNNs) [
8,
9], the deep learning (DL) methods have achieved state-of-art performance in signal and image processing and have been applied to GPR data interpretation [
10]. Liu et al. [
11] proposed an automatic detection and localization method using DL and migration. This method can locate rebars in real time with acceptable accuracy. In order to predict the sizes, shapes, and locations of the subsurface defects, Yang et al. [
12] used a segmentation network named Segnet to map the tunnel-lining internal defects. Segnet can segment the defects in a tunnel lining with better performance than U-net and DeepLab V3+. Qin et al. [
13] introduced a Mask-RCNN based framework to identify steel ribs, voids, and the thicknesses of tunnel linings. This method recognized designated targets with high accuracy yet was not developed for interpreting the actural shapes. Liu et al. [
14] proposed a deep neural network referred to as GPRInvNet to tackle the challenges of mapping the GPR B-scan data to complex permittivity maps of subsurface structures. GPRInvNet can establish a spatial alignment between time-series B-scan data and spatial permittivity maps. Validation was conducted on both the finite-difference time-domain (FDTD) synthetic and physical model testing. The results show that the network is able to reconstruct high-quality relative permittivity maps of subsurface structure from GPR B-scan data. To make the DL network have the ability to invert GPR data with long survey lines, Wang et al. [
15] proposed GPRI2Net. GPRI2Net combines a DenseUnet and a recurrent neural network to exploit the contextual information contained between each data segment in a consecutive and long survey line.
Although the DL methods have demonstrated extraordinary abilities in GPR data interpretation, there are still challenges that hinder the further applications of deep learning methods. Since there are rebars in the near-surface of a concrete structure, the identification of subsurface defects is more difficult. The rebars in the concrete structure act as scatters that generate clutter in GPR profiles and mask the target signatures, making defect echoes beneath the rebars hard to distinguish. In addition, there are many different data processing schemes for GPR B-scan data, and each serves a different purpose. However, most of the existing DL methods only use the original GPR data with gain and noise reduction operations. The GPR data processing step is instrumental for interpreting GPR data. However, current methods cannot effectively utilize the various information contained in GPR data with different data processing methods.
To cope with these problems, many researchers have tried to use different signal processing methods to suppress rebar clutters and decode radargrams. Xiao et al. [
16] proposed a multi-bandpass filter technique to suppress clutters in GPR profiles caused by periodic elements in the near-surface. Wu et al. [
17] reduced rebar echoes in GPR data using hyper-curvelet transform. Wang et al. [
18] proposed a supervised deep learning network for rebar-clutter removal and defect-echo enhancement in GPR images. The results show that the DL-based method is promising for rebar-clutter removal according to its performance and processing speed. However, any supervised learning network has a high level of dependence on a paired dataset. Wang et al. [
19] proposed an unsupervised DL network called the RCE-GAN to remove rebar clutters. Compared to the network proposed by Wang et al. [
18], the RCE-GAN does not need a paired dataset to train the network. Hence, the RCE-GAN is easier to implement because of its lower demand on the training dataset. The detection accuracy of the YOLOv4 network on the RCE-GAN-processed data was improved by 11.9% compared to that on the unprocessed data. Dinh et al. [
20,
21] combined migration and DL to locate rebars in bridge decks. The migration method concentrates the rebar reflected energy to the vertices, which is beneficial to locating rebars in the concrete [
20]. To sum up, the GPR data processing step is instrumental and can improve detection accuracy significantly.
To jointly utilize the strengths of both conventional signal processing and deep learning methods, we proposed a deep learning network to invert processed GPR data to their dielectric properties. The proposed network has three encoder paths and uses the information of three types of GPR data simultaneously. In this work, we first introduce the design of inversion network. Then, we present the three kinds of GPR data and their functions in GPR data inversion. Next, we describe the training and validation of the performance of the network using synthetic GPR data. A comparison study is also reported between the proposed network and a network with a single-path encoder. Finally, we describe a physical experiment that validates the applicability of the proposed network.
2. Methodology
The proposed network
G utilizes the original GPR data
O, the migrated GPR data
M, and the encoder–decoder-processed GPR data
E to infer the permittivity map
P of the concrete structure, which can be denoted by the following expression:
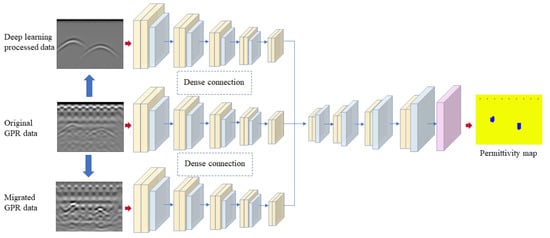
The network’s structure is illustrated in
Figure 1. Three categories of GPR data, including the original, migrated, and encoder–decoder-processed GPR data, are used as the input for the network. A three-path encoder is implemented to process the three kinds of GPR images simultaneously, which extracts three times more information than processing a single GPR image. Dense connections are set between the adjacent encoder paths and allow the network to take advantage of the spatially related information. Then, a decoder network is used to merge all the features obtained by the multi-path encoder and output a permittivity map in accordance with the GPR image.
2.1. Multi-Path Encoder
On the whole, the inversion network has an encoder–decoder structure with three encoder paths. Each encoder path is designed to process one kind of input data. In each encoder path, the input data are first resized to and then passed through a series of convolutional blocks and down-sampling layers. Each convolutional block consists of two convolutional layers, a batch-norm layer, a drop-out layer, and a rectified linear unit (ReLU) layer. All convolution operations apply spatial filters with 1 stride, a dropout rate, and the down-sampling factor of 2. In total, there are four convolutional blocks and four max-pooling layers in each encoder path.
The original, migrated, and encoder–decoder-processed GPR data are used as the inputs of the three encoder paths, respectively. Note that as the migrated and encoder–decoder-processed data are obtained from the original GPR data, the three kinds of GPR data are spatially related, although they are processed with different methods and have different roles. Therefore, we use dense connections between adjacent encoder paths to establish a lateral relationship among the three encoder paths [
22], as shown in
Figure 1b.
Let
denote the output of the
layer in the first encoder path,
be the mapping function, and
and
signify the output and mapping function of the adjacent encoder path. Thus, the output of the
layer can be expressed as
In this kind of connection, all feature outputs are concatenated in a feed-forward manner. Each convolutional block receives the results obtained from the previous one and its adjacent encoder paths. With the dense connections, the network can learn complex relationships between three different kinds of GPR data.
After a series of processing and feature-fusion steps, the encoder produces deep features. Then, a decoder is used to amplify the compressed features to a permittivity map with the same size as the original GPR images by the deconvolutional blocks and up-sampling layers. A total of four deconvolutional blocks with kernels of three and four up-sampling blocks are employed in the decoder network. There is a great deal of low-level information shared between the encoder and decoder, such as the locations of the objects [
23]. Therefore, we shuttle the outputs of the convolutional blocks in each layer of the encoder directly across the net to the corresponding layer of the decoder. After processing by the last layer of the decoder, we apply a convolutional layer to map the features to the number of output channels, followed by a anh function.
2.2. Adversarial Learning and Loss Function
In the training process, we calculate the difference between the outputs of the encoder–decoder network and the ground truth to optimize the network. The L1-distance loss is expressed as
where
x represents the input GPR data,
y represents the ground truth data,
G denotes the encoder–decoder network, and
G(
x) represents the network’s output. The L1-distance loss makes the data reconstructed by the network close to the ground truth in an L1 sense. However, in the process of training, we found that if we only applied L1-distance loss, the network generated blurry results with a roughly correct distribution of relative permittivity values, but the high-frequency details were missing. Thus, we introduced a discriminator to the network. The encoder–decoder network (generator) and the discriminator together form a generative adversarial network (GAN). Now the generator and discriminator are trained jointly, and loss function of the GAN is signified as follows:
In this loss function, the generator aims at minimizing this loss against an adversarial discriminator that tries to maximize it: the generator
G is trained to produce the permittivity map that is indistinguishable from the real distribution, and the discriminator
D is trained synchronously to discern the generator’s fake. As the generator has already generated blurry results, it is wise to make the discriminator only model high-frequency features. Like the method used in [
24], instead of taking the entire image as input, we make the GAN discriminator only classify if the
patches in an image are real or fake. This motivates the GAN discriminator to only model high-frequency features. We run this discriminator convolutionally across the image, averaging all responses to provide the ultimate output of
D. The structure of the GAN discriminator is shown in
Figure 2. The combination of the L1-distance loss and GAN loss is used as the loss function of our inversion network:
where the
is a balancing parameter that controls the relative importance of the two parts. In our study, to correctly reconstruct the permittivity map has higher priority, so the L1-distance loss should account for a larger share of the loss function. The
is taken as 10 in this study.
5. Laboratory Experiment
In this section, we demonstrate the effectiveness of our inversion approach using the GPR data acquired from a physical model experiment to validate the practicality of the proposed method on real-world GPR data.
As shown in
Figure 9a, we built a reinforced concrete model with dimensions of 1.0 m × 2.0 m (height × width). From the top to bottom, the model consisted of three layers, including reinforced concrete, plain concrete, and sand with thicknesses of 0.6, 0.25, and 0.15 m, respectively. Inside of the reinforced concrete layer, there were three voids denoted as V1, V2, and V3. The voids were made of cubic wooden boxes, and the side lengths were 0.2, 0.1, and 0.2 m, respectively. The burial depths of three voids were 0.37, 0.47, and 0.36 m, respectively. Inside this layer there were two rows of equally spaced rebars, 22 mm in diameter, and with a spacing of 33 cm. The depths of the two layers of rebars were 5 and 55 cm, respectively. We used the pulse EKKO PRO GPR system equipped with a 500 MHz center frequency antenna to obtain GPR data. The time window was set as 30 ns, the sampling rate was 100 trace/m, and the length of the survey line was 2.0 m.
As shown in
Figure 9b, we obtained a raw GPR image from the model experiment. Prior to inverting the GPR image using the proposed network, pre-processing was performed on the raw data. The pre-processing operations included time-zero correction, direct-current (DC) shift removal, time-varying gain, frequency filtering, and time window trimming. First, we adjusted the starting time of the GPR data to view the air–concrete surface. Then, we removed the DC component by subtracting the mean value of each trace. Next, we used the time-varying gain with the exponential function to compensate for the attenuation of GPR signals. After that, we suppressed the noise using a 1D band-pass filter with lower and upper cut-off frequencies of 200 and 650 MHz, respectively. Finally, we trimmed the time window to 20 ns.
After pre-processing, we obtained the original GPR data for the inversion plotted in
Figure 10a. Next, we migrated the original GPR data with migration velocity of 0.094 m/ns and achieved the minimum entropy value of 1.2866. The migrated GPR image is demonstrated in
Figure 10b. We also processed the original GPR data using the rebar elimination network and obtained the rebar clutter eliminated GPR image depicted in
Figure 10c.
We fed the three GPR images into the proposed network and obtained the inversion results shown in
Figure 10d. The relative positions of all three voids are almost identical to those in the ground truth. Additionally, all eight rebars were reconstructed in the correct locations. The sizes of the voids V1, V2, and V3 in the inverted permittivity map were
,
, and
cm (width × height), respectively. Compared with the inverted positions, the accuracy of the void sizes is lower, which is caused mainly by two reasons: (1) Limited by time, cost, and other factors, we only used the FDTD synthetic GPR data as the training data. The FDTD model we built is different from the real situation, due to the inhomogeneity of the concrete medium, the attenuation of the signal, electromagnetic interference, etc. (2) The quality of the deep-learning-processed GPR data is affected by rebar clutters in the original data. However, the result is still promising, since all the voids were successfully reconstructed in their correct positions. More high-quality and well-labeled training data are needed to improve the performance of the proposed network on real-world GPR data.
6. Conclusions
In this research, a novel deep learning network with a multi-path encoder was proposed for the interpretation of GPR data. The network takes three kinds of GPR data as the input and outputs the permittivity maps of the subsurface. With the multi-path encoder, the network makes use of the information contained in the three types of GPR data all at once. The dense connection between the adjacent encoder paths makes the network take advantage of the spatially related information. Compared to conventional neural networks that only utilize one type of data, the proposed network has improved the inversion accuracy. On the synthetic GPR dataset, the average IoUs of the proposed network were 0.6108, 0.4288, and 0.8397 for void, crack, and untightness detection, higher than those of the conventional single-path encoder network, which were 0.5088, 0, and 0.3699, respectively. We also verified the proposed network on real-world data obtained from a physical experiment, in which the network detected the near-surface rebars and voids precisely.
Limited by time and cost, we collected an insufficient amount of real-world GPR data. Future directions of this research include: (1) to design a physical model to obtain sufficient high-quality and well-labeled GPR data to train and validate the proposed network; and (2) to improve the FDTD simulation method to create synthetic GPR data with high fidelity.