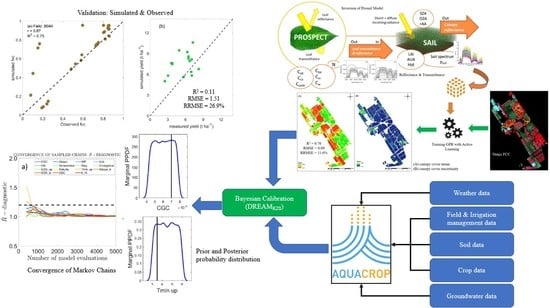
Bayesian Calibration of the Aquacrop-OS Model for Durum Wheat by Assimilation of Canopy Cover Retrieved from VENµS Satellite Data

Abstract

Crop growth models play an important role in agriculture management, allowing, for example, the spatialized estimation of crop yield information. However, crop model parameter calibration is a mandatory step for their application. The present work focused on the regional calibration of the Aquacrop-OS model for durum wheat by assimilating high spatial and temporal resolution canopy cover data retrieved from VENµS satellite images. The assimilation procedure was implemented using the Bayesian approach with the recent implementation of the Markov chain Monte Carlo (MCMC)-based Differential Evolution Adaptive Metropolis (DREAM) algorithm DREAM_(KZS). The fraction of vegetation cover (fvc) was retrieved from the VENµS satellite images for two years, during the durum wheat growing seasons of 2018 and 2019 in Central Italy. The retrieval was based on a hybrid method using PROSAIL Radiative Transfer Model (RTM) simulations for training a Gaussian Process Regression (GPR) algorithm, combined with Active Learning to reduce the computational cost. The Aquacrop-OS model was calibrated with the fvc data of 2017–2018 for the Maccarese farm in Central Italy and validated with the 2018–2019 data. The retrieval accuracy of the fvc from the VENµS images were the Coefficient of Determination (R²) = 0.76, Root Mean Square Error (RMSE) = 0.09, and Relative Root Mean Square Error (RRMSE) = 11.6%, when compared with the ground-measured fvc. The MCMC results are presented in terms of Gelman–Rubin R statistics and MR statistics, Markov chains, and marginal posterior distribution functions, which are summarized with the mean values for the most sensitive crop parameters of the Aquacrop-OS model subjected to calibration. When validating for the fvc, the R² of the model for year (2018–2019) ranged from 0.69 to 0.86. The RMSE, Relative Error (RE), Relative Variability (α), and Relative Bias (β) ranged from 0.15 to 0.44, 0.19 to 2.79, 0.84 to 1.45, and 0.91 to 1.95, respectively. The present work shows the importance of the calibration of the Aquacrop-OS (AOS) crop water productivity model for durum wheat by assimilating remote sensing information from VENµS satellite data.

1. Introduction

Spatial crop yield information is valuable both for crop management and for market forecasting [1]. These data only reside in the administrative units. The data is useful but does not provide information on the scale of the field nor on the variability within the field, which is essential to inform field-specific decision-making for the different sectors, including farmers, crop insurance companies, and food trading agencies [2]. Clear, large-scale yield estimates at the individual field level are therefore an important activity for research and application in agriculture [3].

Remote sensing-based crop yield estimation methods roughly fall into two categories: empirical or based on crop models, the latter including data assimilation approaches [4,5,6,7]. Empirical methods generally require training of parametric or non-parametric regression algorithms with in situ data, which are generally available at a coarse resolution. Thus, these methods provide yield data at a coarse resolution [2,8]. A few studies [2,9,10] attempted to produce fine-resolution yield maps using Landsat satellite data by training machine learning regression algorithms with the synthetic yield data; these methods were computationally efficient but suffered from potential bias, especially when the synthetic samples were not adequate representatives of the real-world conditions.

Simulation of crop growth models is an important tool for research and management in ecology, agriculture, and the environment. These models are used to simulate soil-cultivation system actions in response to climate and agricultural management [11,12,13]. Agricultural processes, crop interaction with the atmosphere, and soil over time are described by theoretically based mathematical equations and empirical studies. Such equations and parametrizations necessarily require truth assumptions, leading to confusion and inaccuracy of the output variables [14]. Regardless of the model used, the identification of the parameters that most affect the output is a fundamental problem for most of the environmental applications when great uncertainty is expected about their values, for example in regional applications [15,16,17]. The system parameters, therefore, need to be calibrated before they refer to regional scenarios. To this end, the integration of crop growth models and remote sensing data is attracting even greater interest in research [18]. Noteworthy, higher spatial and temporal resolution remote sensing data improves the predictive power of the calibrated model.

The most common approach for model calibration is based on optimization techniques. Various optimization methods have been used and the crop model parameters are typically obtained after the cost function between the simulations and the measured data has been minimized [18]. There have been different algorithms implemented for model calibration, e.g., particle swarm optimization, simplex, least square, genetic algorithms and shuffled complex evolution, and four-dimensional variational data assimilation (4D-Var) [18,19,20,21,22]. One of the drawbacks of these algorithms is that they can get trapped into local optima due to the complexity of the optimization problem. Additionally, they only provide point estimates of the parameters, without indications of their uncertainty, e.g., not providing confidence intervals. Calibration techniques that follow a Bayesian formalism, as an alternative optimization method, include a posterior distribution of the model parameters. These can be derived by conditioning the model’s spatio-temporal behavior on measurements of the system response observed [23]. If the prior distribution and the probability function have been established, the posterior distribution can be summarized by, for example, the mean, covariance, or percentiles of individual parameters. Summarizing the posterior distribution is not analytically feasible for complex dynamic system models, such as crop models, which are highly non-linear, and Monte Carlo (MC) simulation methods are needed to generate a sample of the posterior distribution [23].

The earliest Markov chain Monte Carlo (MCMC) method, i.e., the random walk Metropolis (RWM) algorithm, was developed by [24]. In this method, a candidate parameter value is initially sampled from a distribution of asymmetric proposals, centered around the current state of the Markov chain. The Metropolis probability is then computed for this candidate. When the candidate is approved, the chain must switch to the new candidate otherwise the chain must remain in the current state. By repeating this procedure, the Markov chain results in an equilibrium distribution of the parameter. In [25], the RWM algorithm was generalized by implementing an unequal probability density of the forward and backward jumps; it has become one of the most revolutionary algorithms in computational statistics and is called the Metropolis–Hastings (MH) algorithm [26].

In recent decades, much work has been dedicated to enhancing the performance of the MCMC methods and enhancing the original RWM and MH algorithms. These are multi-chain and single-chain approaches. Single-chain methods work a single trajectory and multi-chain methods use various parallel trajectories to investigate the posterior distributions of the targets. The most common single-chain approaches are adaptive proposals [27], adaptive Metropolis [28], and delayed rejection adaptive Metropolis [29]. The use of multiple chains provides robust protection against premature convergence and provides a wide range of statistical measures to test whether convergence has been achieved to a restrictive distribution [30]. The most widely used multiple-chain methods are the Shuffled Complex Evolution Metropolis algorithm (SCEM-UA) [31] and Differential Evolution Markov Chain (DE-MC) [32]. Using adaptive randomized subspace sampling, multiple chain pairs for proposal development, and explicit consideration of aberrant trajectories, the efficiency of the DE-MC approach has been increased. This new method called Differential Evolution Adaptive Metropolis (DREAM) [33] maintains the detailed balance and ergodicity and has demonstrated excellent performance on a wide range of issues, including nonlinearity, high dimensionality, and multimodality [34].

Some extensions were also developed based on DREAM, e.g., DREAM_(ZS) and MT-DREAM_(ZS), suitable for high-dimensional problems [34,35], as well as DREAM_(D) for discrete and combinatorial posterior distribution problems [36] and DREAM_(ABC) for diagnostic model evaluation [37], etc.

We use DREAM_(KZS) in the present work, which is an extension to DREAM_(ZS) and explicitly designed to accelerate the convergence of DREAM_(ZS) in exploring the high-dimensional target distributions. The new proposal distribution is based on the simpler ensemble updating scheme [38], which only updates the model parameters by assimilating all historical measurements. The information found in the model parameter covariance structure, the measurements, and model performance is used in the Kalman jump. So, the Kalman jump can generate a more directional update of the model parameters than the parallel direction jump and the snooker jump in DREAM_(KZS) [39]_.

Durum wheat is one of Italy’s key crops and therefore improving crop yield simulation efficiency is critical in addressing the challenges of precision farming, such as managing fertilization and predicting yield before harvest. Previous studies have mainly focused on optimization methods with satellite data or ground data [40]. Integration with crop models, e.g., with the Aquacrop model [41], originally developed by the Food and Agriculture Organization (FAO) of the United Nations to simulate crop yield responses to water, has been shown to provide promising results [42]. Aquacrop simulates daily canopy cover, biomass, and yield as a function of water productivity. The open-source version of the Aquacrop model (AOS) was developed by [43], and recently a new version of the AOS, AOS v6.0a [44], has been made available.

Given the importance of model calibration, our interest was that of assessing the value of high temporal and spatial frequency remotely sensed data for the calibration of the AOS model on durum wheat. The aim of this study was thus to find the optimal values of the AOS model parameters for the study site and assess the Aquacrop-OS model performances by exploiting the fvc retrieved from high spatial and temporal resolution VENµS satellite images. We implemented the state-of-the-art Markov chain Monte Carlo-based DREAM algorithm, DREAM_(KZS), to get a Bayesian inference on the crop model parameters for durum wheat, which is the predominant crop in our study region of the Maccarese farm in Central Italy. Calibration and validation were carried out separately using the fvc from the VENµS images: The calibration was developed in 2017–2018 for the fvc while the validation was carried out in 2018–2019 for the fvc for the different fields of the farm.

2. Materials and Methods

The overall workflow is presented in Figure 1.

2.1. VENµS Satellite Data

VENµS (Vegetation and Environment monitoring micro-Satellite) is a joint Earth observation mission of Israel and France’s space agencies. It was launched in August 2017 with an expected life span of 3 years. VENµS satellite data is of high temporal (2 days) and spatial resolution (5.3 m) and is acquired on about 100 sites all around the world [45]. It operates in 12 spectral bands from visible to near-infrared, suitable for vegetation studies. Due to the signal-to-noise ratio, the Level 2A data, i.e., after atmospheric corrections, were provided at 10 m (https://theia.cnes.fr/). In this work, VENµS 10 m atmospherically corrected surface reflectance data were used to carry out the processing. This 10 m data for the period November 2017–June 2018 and November 2018–June 2019 were used for the retrieval of the fvc for our study site (see Section 2.2). Currently, the full archive is being re-processed to provide the data at 5 m. The VENµS satellite bands are reported in

Table 1. VENµS satellite bands information.

Bands	Central Wavelength (nm)	Bandwidth (nm)	Main Applications
B1	420	25	Atmospheric Correction Water
B2	443	40	Aerosols, Clouds
B3	490	20	Atmospheric Correction, Water
B4	555	20	Land
B5	638	24	Vegetation Indices
B6	638	24	DEM, Image Quality
B7	672	16	Red Edge
B8	702	24	Red Edge
B9	742	16	Red Edge
B10	782	16	Red Edge
B11	865	20	Vegetation Indices
B12	910	20	Water Vapor

.

2.2. Retrieval of fvc from VENµS Satellite Data

The PROSAIL model [46] is a widely used Radiative Transfer Model (RTM) for generating realizations of top of canopy reflectance by considering the measured biophysical variables of the crop of interest. The PROSAIL model’s parameter ranges, statistical distribution, and the number of classes were similar to those used in previous research on the biophysical variables for the same study area [47]. A total of 7 out of the 12 bands (band 4,5,7–11) were selected from the VENµS satellite data that best approximates the Sentinel-2 8 bands suitable for vegetation studies [48]. Resampling of the PROSAIL simulations of the VENµS satellite selected bands and the addition of Gaussian noise was performed to better represent the actual reflectance of the canopy, simulated by the RTM. The detailed process is described by [47], to which interested readers are referred.

In a previous comparative study of multiple hybrid machine learning algorithms based on PROSAIL simulations, for the biophysical variables retrieval from Sentinel-2, Gaussian Process Regression (GPR) with Active Learning (AL) was found to be the best algorithm [47]. We used here the same implementation with the sampling changed from Sentinel-2 to the VENµS bands for the retrieval of the fvc from VENµS satellite data.

2.3. Smoothing and Fitting fvc Time Series Data Retrieved From Venµs Satellite Data

The fvc time series was retrieved from the VENµS data for two years of the durum wheat growing seasons. Initially, the fvc time series were interpolated into daily time intervals using a 4253H twice filter [49], and then a double logistic function was used to fit the data [50]. The 4253H twice is a median filter that takes the running median of 4, then 2, then 5, and then 3 data points over the fvc time series followed by a running weighted average. This procedure is repeated with the residuals and then both the results are added together [51]. Finally, the peak values were retained by scaling the fvc time series to the maximum of the un-smoothed fvc time series (see Results section).

2.4. Study Site and Ground Validation Campaigns

The test site of Maccarese (Figure 2) was used in the present study. Maccarese (41.833° lat. N, 12.217° long. E, 8 m a.s.l.) is a private farm of 3200 ha in a flat area with large fields, located on the west coast of Central Italy, near Rome. Field campaigns to measure the LAI of the durum wheat (Triticum durum Desf.) crops were carried out for this location from January 2018 to April 2018 at dates close to the VENµS acquisitions. The variables were sampled according to an Elementary Sampling Unit (ESU) scheme, to capture the variability within and among the different fields. Each ESU consisted of a quadrat 20 m by 20 m in size, to easily accommodate the VENµS 10 m pixel resolution. A total of 15 ESUs, placed at different locations, were employed at the different sampling dates. Each of the ESUs contained nine points, where the LAI measurements were collected. The LAI was measured using a LAI-2000 or LAI-2200C Plant Canopy Analyzer (LI-COR, Lincoln, NE, USA). Since LAI 2000/220C measurements were not always acquired under diffuse light conditions, data were pre-processed by applying the recommended scattering correction procedure [52].

LAI 2000/2200C measurements were used to derive the fvc, by using the following equation [53]:

$$fvc= 0.94 \times {\left(1 -e^{-0.43 \times \mathrm{LAI}}\right)}^{0.52}$$

(1)

Table 2. Description of the calibration and validation datasets.

AOS Model Calibration Data	AOS Model Validation Data
fvc time series of 2017–2018 retrieved from VENµS data(20 pixels that represents yield variability)	fvc time series of 2018–2019 retrieved from VENµS data biomass measured on the ground for the years 2017–2018 yield observed from the combine for the years 2017–2018

presents the calibration and the validation datasets and

Table 3. VENµS acquisitions and ground measurements dates.

Date—Ground Measurements	Date—VENµS Acquisition	Difference (Days)
31 January 2018	28 January 2018	3
16 February 2018	13 February 2018	3
6 April 2018	8 April 2018	2
20 April 2018	20 April 2018	0

shows the dates of the VENµs satellite data acquisitions close to the ground data collection dates.

The aboveground biomass was collected on two different dates, 16 February and 20 April in the year 2018, in eight different ESUs in different fields (see Figure 2a). The samples were collected destructively at the center point of each ESU within an area of 1 m² and were subsequently oven-dried at 72 °C for three days. Finally, the dried samples were weighted and the biomass data was used to compare the results of the calibration. The yield data was obtained from a New Holland CX860 combine harvester, equipped with a yield mapping system. The data were pre-processed by removing the spatial outliers and points where the speed of the machine was less than 0.5 km h⁻¹. All points having a yield greater than 15 t ha⁻¹ and less than 0.2 t ha⁻¹ were also removed from the processing. Further, very low yielding values were removed among the adjacent high-yield passes, which indicated that the operator was not working at full cutting width. As a next step, block kriging was carried out using a local variogram option; this processing was completed in the open-source software Variogram Estimation and Spatial Prediction with Error (Vesper), developed by the Australian Center for Precision Agriculture [54]. The final yield map produced after corrections and processing was used for pixel-wise validation of the yield predictions obtained after calibration on the same year (2017–2018 cropping season).

2.5. Weather Data

The meteorological data used in this study to drive the model simulations were obtained from a weather station at about 3 km from the farm, from the Agrometeorological Service of the Lazio Region. For the period 2017–2019, the daily minimum and maximum temperature, relative humidity, wind speed, rainfall data, and daily solar radiation were provided. The measurement of the regular reference evapotranspiration was based on the FAO Penman–Monteith method, as described in [55], and the ET0 calculator [56]. Figure 3 shows the minimum and maximum temperature, rainfall, and reference evapotranspiration for the 2017–18 and 2018–19 durum wheat growing seasons (October to July) at the Maccarese site.

2.6. Aquacrop-OS Model and Sensitive Parameters

The Aquacrop crop water productivity model was introduced by [41]. It simulates the relationship between crop yield and crop transpiration under different conditions. Aboveground biomass is simulated daily by using the normalized crop water productivity (NCWP) concept. Biomass (bio) is obtained as the product of the NCWP to the ratio of crop transpiration (CT) and reference evapotranspiration (ET0; Equation (2)):

$$bio=NCWP \times \sum \frac{CT}{E{T}_o}$$

(2)

Grain yield (yld) is obtained by multiplying the harvest index (HI) by bio (Equation (3)):

$$yld=bio \times HI$$

(3)

The Aquacrop model originally developed by FAO includes a graphical user interface to run the model, but there have been different versions developed, including a command-line plug-in version and a GIS version (see http://www.fao.org/aquacrop). This model has been tested on different climates, geographical locations, and crops under different irrigation and field management practices [57,58,59,60,61]. To allow the customization of the model and to implement the model for different data demanding applications, an open-source Matlab version, Aquacrop-OS (OS), was developed by [62]. The latest version of AOS, Aquacrop-OS v6.0a, is used in the present study. Since AOS is slightly different from the original FAO version in terms of parameters, specific sensitivity analyses and calibrations should be carried out since the studies carried out on the standard FAO Aquacrop model cannot be directly applied to AOS.

In previous work on the AOS sensitivity analysis, [63] applied two different methods: the moment independent density-based PAWN and variance-based Extended Fourier Amplitude Sensitivity Test (EFAST). A common set of the most influential parameters was found with both methods, although the rankings of the parameter varied for the same study site. In the present work, we considered the same set of parameters and parameter ranges for the Bayesian calibration, using the DREAM_(KZS) version of the DREAM algorithm originally developed by [23].

2.7. Markov Chain Monte Carlo-Based DREAM_(KZS) Algorithm

The Bayesian estimation aims to update the distribution of the critical parameters by combining observations and prior values [64]. Bayes theorem states that, given the new observations, the posterior probability of a hypothesis is proportional to the product of the prior probability of the hypothesis and likelihood of the same hypothesis. By adopting a Bayesian formalism, the posterior distribution of the model’s parameters can be derived by conditioning the model’s spatio-temporal behavior on measurements of the system response observed:

$$p\left(x|\tilde{Y}\right)= \frac{p\left(x\right)p(\tilde{Y}|x)}{p\left(\tilde{Y}\right)}$$

(4)

where p(x) and p(x|$\tilde{Y}$) signify the prior and posterior parameter distribution, respectively, and L$\left(x|\tilde{Y}\right)$=p($\tilde{Y}$|$x$) denotes the likelihood function. If the parameters are well defined in the prior distribution, the key issue is the interpretation of the likelihood function. L$\left(x|\tilde{Y}\right)$ is used to summarize the difference between the simulations of the model and the data of the measurements. If the error residuals are assumed to be uncorrelated then the likelihood of the n-vector of residual error can be written as follows:

$$L\left(x|\tilde{Y}\right)=f_{{\tilde{y}}_1}\left(y_1\left(x\right)\right) \times f_{{\tilde{y}}_2}\left(y_2\left(x\right)\right)\times \dots \times f_{{\tilde{y}}_n}\left(y_n\left(x\right)\right)= {\displaystyle \prod }_{t=1}^n{f}_{{\tilde{y}}_t}\left(y_t\left(x\right)\right)$$

(5)

where ${\mathrm{f}}_{\mathrm{a}}\left(\mathrm{b}\right)$ signifies the probability density function of a evaluated at b, given that a and b represent the calculation of the likelihood function at each measurement. If we assume further that the residuals of the error are normally distributed, then Equation (5) can be written as

$$L\left(x|\tilde{Y}, {\widehat{\sigma }}^2\right)={\displaystyle \prod }_{t=1}^n\left(\frac{1}{\sqrt{2\pi {\widehat{\sigma }}^2}}exp\left[-\frac{1}{2}{\left(\frac{{\tilde{y}}_t-y_t\left(x\right)}{{\widehat{\sigma }}_t}\right)}^2\right]\right)$$

(6)

where an n-vector with standard deviations of the measurement error of the observations is ${\widehat{\sigma }}_t$={${\widehat{\sigma }}_1, \dots ., {\widehat{\sigma }}_n$}. This formulation allows for homoscedastic and heteroscedastic measurement errors.

The posterior distribution is often high dimensional and analytically intractable for complex crop models, and sampling methods are required to estimate the target, and then the desired description of the posterior distribution can be obtained from the sample [65]. To generate samples from the posterior distribution, a lot of iterative methods have been developed. In a way, all of these methods rely on Monte Carlo simulations. As already stated, we implemented the DREAM_(KZS) algorithm [39] for parameter estimation in this work.

2.8. Statistical Analysis and Validation

$\widehat{R}$ statistics, as proposed by [30], was used to determine when the convergence of the sample chains to a limiting distribution has been achieved. This analysis compares the within and between chain variance for each parameter using

$${\widehat{R}}_j= \sqrt{\frac{N+1}{N}\frac{{\widehat{\sigma }}_{+}^{2\left(j\right)}}{W_j}-\frac{T-2}{NT}}$$

(7)

where N is the number of chains, T implies the number of samples in each chain, Wj is the within chain variance, and ${\widehat{\sigma }}_{+}^{2j}$ is an estimate of the variance of the jth parameter of the target distribution

$${\widehat{\sigma }}_{+}^{2\left(j\right)}= \frac{T-2}{T} W_j+ \frac{2}{T} B_j$$

(8)

For each parameter j = {1, …, d}, to declare convergence, ${\widehat{R}}_j$ should be ≤ 1.2, or otherwise the value of T should be increased and the chains should run longer. Since the various N chains are launched from different starting points, the $\widehat{R}$ diagnostic is a relatively robust estimator [24] (see Results section).

The accuracy of the fvc retrieval using VENµS satellite data is computed in terms of Coefficient of Determination (R²), Root Mean Square Error (RMSE), and Relative Root Mean Square Error (RRMSE). Bayesian calibration of the AOS model was carried out using the fvc time series data for multiple pixels (center pixels of ESU) from eight fields for the years 2017–2018 (Figure 2a) and validation was carried out for seven fields for the years 2018–2019 (Figure 2b). Different metrics, namely, the RMSE, Relative Error (RE), Relative Variability (α), Relative Bias (β), Linear Correlation Coefficient (r), and Kling–Gupta Efficiency (KGE), were used to assess the performance of the validation. As indicated by [66], the significant metric Normalized Standard Error (NSE) can be divided down into three distinctive components: a linear correlation between simulations and observations, β normalized by the standard deviation in the observed values, and α as a measure of the relative variation in the simulated and observed values. In [66], KGE is defined as

$$\alpha = \frac{{\sigma }_s}{{\sigma }_o}$$

(9)

$$\beta = \frac{{\mu }_s}{{\mu }_o}$$

(10)

$$KGE= 1-\sqrt{{\left(r-1\right)}^2+{\left(\alpha -1\right)}^2+{\left(\beta -1\right)}^2}$$

(11)

where σ is the standard deviation and µ is the mean value (with the subscript “s” for simulations and “o” for observations), α is the relative variability, and β is the relative bias. For calibration, we have used the fvc time series of the years 2017–2018 and one simulation for each pixel and applied the process to multiple pixels in each field presented in Figure 2a. The pixels selected were the center point of each ESU where the biomass sample was collection on the ground. Parameter values obtained by the calibration process were used for fvc validation for the years 2018–2019 and we have a single simulation for validation (Figure 2b). The simulated biomass and yield for the years 2017–2018 were also validated with the ground-measured biomass and the yield data measured at the end of the season.

3. Results

3.1. fvc Retrieval

The advantage of using the GPR algorithm is that it also estimates associated uncertainty along with the mean values of predictions (fvc). The fvc time series of a pixel as an example is shown in Figure 4b; the shaded region represents the uncertainty in the estimation. It can also be visualized that the uncertainty is higher at the peak in comparison to the start or end of the growing season. The sudden dip in the fvc value (Figure 4b) at the peak represents the partial cloudy date and so it makes the smoothing and the fitting of the fvc time series necessary before further processing of assimilation. Figure 4c shows an example of the fvc time series of a pixel with the fvc retrieved from VENµS satellite data, which has partially the effects of the cloud; this original fvc time series was processed using a 4253H twice filter followed by fitting a double logistic function to this data to obtain smooth fvc time series data, which will be ingested in the assimilation procedure.

An example of fvc mean estimation maps with the associated uncertainty expressed as the standard deviation (SD) around the mean and the relative uncertainty expressed as the coefficient of variation (SD/mean) for four dates for the durum wheat fields, as shown in Figure 5a (mean fvc), Figure 5b (associated uncertainty), and Figure 5c (relative uncertainty).

It can be seen from Figure 5a,b that the uncertainty increases during the peak fvc mean estimates, which can also be assessed in Figure 4b. Relative uncertainty (Figure 5c) may provide a more meaningful interpretation. It can be observed that the fallow areas or bare soil retrievals have a rather high relative uncertainty. By applying a threshold, the more uncertain retrievals can be masked out. Hence, uncertainty can function as a spatial mask that enables displaying only pixels with a high certainty [67].

3.2. Parameters Identification

Figure 6a,b represents the evolution of the univariate and multivariate $\widehat{R}$ statistics of the 15 crop model parameters, as proposed by [30] for the analysis of the convergence. The threshold of 1.2 for convergence diagnosis is represented by the black dashed line.

To better explore the parameter space, we run N = 4 parallel chains in DREAM_(KZS). The length of the chain was set as 5000, which means that the total number of model evaluations became 20,000 (5000 × 4). We restrict the Kalman jump to the initial 20% of the simulation time as it cannot maintain a detailed balance and set the probabilities of using the Kalman jump, the parallel direction jump, and the snooker jump to 20%, 72%, and 8%, respectively, while in the remaining 80% simulation, these are set 0%, 90%, and 10% to sample the posterior, which can satisfy a detailed balance with diminishing adaptation [39]. When the $\widehat{R}$ statistic of all the 15 parameters is below 1.2, it can be concluded that the Markov chains converge to the equilibrium distribution. The number of chains and the number of generations for each chain is sufficient for the mixing of the chains and the exploration of the entire parameter space.

Figure 7 presents the marginal posterior probability density functions (PPDF) of the parameter estimates when the sampling process had achieved a stationary distribution at the end of the process. It can be visualized from Figure 7 that the prior distribution function has been transformed to the posterior distribution function for all the AOS model parameters subjected to the calibration.

Prior ranges of the model parameters (uniform distribution) and the final value after processing of the DREAM_(KZS) algorithm are presented in

Table 4. Prior ranges and parameter values computed from the posterior distribution (mean) of the 15 parameters of the AOS model used for calibration.

Parameter	Unit	AOS Standard	Prior Range	Estimated Parameter
CGC	fraction GDD	0.0050	(0.0042, 0.0078)	0.0060
HIstart	GDD	1250	(1090, 1395)	1243
WP	gm−2	15	(11, 22)	16.50
Kcb	-	1.10	(0.77, 1.43)	1.10
HI0	%	0.48	(0.32, 0.59)	0.46
Senescence	GDD	1700	(1090, 2250)	1670
Wpy	gm−2	100.00	(75, 125)	100.00
Emergence	GDD	150	(90, 230)	160
GDD_up	GDD	14	(9, 18)	13.50
Maturity	GDD	2400	(1590, 3150)	2370
Tmin_up	°C	5	(3, 6)	4.50
fshape_b	-	13.81	(9.6694, 17.9575)	13.81
GDD_lo	GDD	0	(0, 5)	2.5
CDC	fraction GDD	0.0040	(0.0028, 0.0052)	0.0040
b_HI	-	7	(3, 6)	4.50

. Since the output of the DREAM_(KZS) algorithm used for calibration is a posterior distribution, rather than a single point estimate, the mean value of all the 15 crop model parameters was extracted from the marginal posterior distribution function, as is most commonly used. Although the calibration was carried out using fvc data from eight different durum wheat fields for the years 2017–2018, the parameter values do not differ much among each field. The mean values of the posterior distribution across fields are thus presented in Table 4.

3.3. Calibration and Validation

3.3.1. fvc

Error metrics for the estimation of the fvc for the validation fields presented in Figure 2b, for the years 2018–2019, are presented in

Table 5. RMSE, RE, α, β, r, and KGE for validation of the fvc years 2018–2019.

Field Code	RMSE	RE	α	β	r	KGE
B031	0.16	0.25	1.11	1.03	0.87	0.18
B032	0.19	0.60	0.96	1.07	0.83	0.15
B044	0.20	0.44	1.11	1.13	0.87	0.22
B062	0.41	2.79	0.84	1.9	0.61	0.93
B069	0.44	2.29	0.88	1.95	0.52	0.97
B085	0.23	0.65	0.96	1.30	0.86	0.33
B109	0.15	0.19	1.45	0.91	0.93	0.47

. The calibration of the Aquacrop model was previously performed by [68] with two years of canopy cover data retrieved from MODIS LAI images and validated on one year of data for two farms in Italy; the error metrics have more or less similar values, but the linear correlation coefficient is higher in this work (Table 5).

From Table 5 it can be seen that r is close to 1, except for the two fields: Field B062 and Field B069, where it has a value of 0.61 and 0.52. This shows that the linear relation between the observed and simulated fvc time series is strong. Figure 2b shows the background image of the VENµS data on 12 March 2019, where the fields B062 and B069 can be seen clearly as fallow lands. The not so strong correlation for these two fields may be the difference between the sowing and planting dates in comparison to the other fields. This can also be understood from the RMSE and RE data from Table 5, where it has the highest error for these two fields on validation, i.e., 0.41 and 0.44 for RMSE and 2.79 and 2.29 for RE. α and β are the representative for the relative variability and relative bias, and their values range from 0.84 to 1.45 and 0.91 to 1.95, respectively. The value of α is close to 1 for almost all the fields, which is the ideal value for it; similarly, β also has values close to 1, to its ideal value except for the fields mentioned earlier. KGE, which combines α, β, and r in an equation to find out the efficiency of the validation, ranges from 0.15 to 0.93, which is higher than during the calibration (metrics not shown).

The calibrated values of the 15 AOS model parameters from Table 4 were used with the other model parameters set as default to generate the fvc, biomass, and yield time series data for the years 2018–2019. This simulated fvc time series is represented as a green curve in Figure 8. As can be seen, the curve is the same for all the fields; this is because we generated a single set of simulations for the years 2018–2019 that is representative of the average fvc in the study area (Figure 2b). The field-wise average fvc time series derived from the VENµS satellite images for the years 2018–2019 were plotted with this simulated fvc time series. The results are mentioned in Table 5; it can also be visually assessed from the Figure 8—the R² ranges from 0.69 to 0.86 and r from 0.83 to 0.93. There is a good agreement between the simulated fvc time series and VENµS satellite image-derived fvc time series.

3.3.2. Biomass and Yield

The biomass collected inside the ESU on two dates (16 February 2018 and 20 April 2018) and yield data collected by the combine on multiple pixels in different fields in 2018 were compared with the simulation predictions obtained after the pixelwise calibration carried out using VENµS fvc (Figure 9a,b). As can be seen visually, the simulated biomass is overestimated in comparison to the ground, and the pixelwise yield predictions shows low error when compared to the measured yield (RMSE of 1.51 t ha⁻¹), with a tendency towards overestimation that is less pronounced than for biomass. Although AOS overestimated biomass and to a lesser extent yield as compared to the ground measurements, it is in good agreement with the fvc (Figure 8), confirming the importance of the calibration.

4. Discussions

4.1. fvc Retrieval

The R² obtained was 0.76, the RMSE 0.09, and the Relative RMSE (RRMSE) was 11.6 (%), with an apparent overall slight overestimation of high values and underestimation of low values in the retrieval. Due to the Bayesian backbone of the GPR family algorithms, the advantage of using the GPR algorithm for the estimation of the fvc is that it provides uncertainty intervals associated with the mean predictions, which are reported as vertical bars in Figure 4a, whereas the horizontal bars show the variability (in terms of standard deviation) within single ESUs.

The original fvc data retrieved from the VENµS data using the GPR algorithm, which sometimes showed an erratic seasonal pattern (Figure 4c), were smoothed using the 4253H twice filter, fitted using a double logistic function [50] and then rescaled to the minimum and maximum of the original fvc time series retrieved using GPR. Since the goal of the present work was to get the Bayesian inference on the AOS crop model parameters subjected to calibration, we considered this retrieval of fvc from the VENµS satellite 10 m data to be acceptable. Maps of the fvc for the Maccarese farm were obtained for 15 cloud-free VENµS images acquired from 2017 to 2018 and 27 images acquired for the 2018–2019 wheat growing seasons. An example fvc mean estimation maps with associated uncertainty and relative uncertainty for four dates for the durum wheat fields is shown in Figure 5. The related uncertainty images (Figure 5b) indicate higher retrieval certainties from the trained model in the low-intensity blue color. When applied to any image, the generation of uncertainty estimates allows insight into the pixel-by-pixel approach. It thus enables the definition for which land covers are correlated with a high degree of certainty and also those areas in which additional sampling would gain land cover. [67].

Uncertainty (σ) is also correlated with the mean estimate (µ). Relative uncertainties (σ/µ) can give a more meaningful interpretation (Figure 5c). It can be observed that there is a relatively high relative uncertainty regarding fallow areas or bare soil retrievals. The application of a threshold will cover some more questionable retrievals. Uncertainty can, therefore, act as a spatial mask that only display pixels with a high degree of certainty [67].

A similar approach of biophysical variables retrieval utilizing Sentinel-2 data was implemented by [47]. The accuracy that they found was somewhat higher than in this work, possibly because in [47] a choice of optimal bands was made following the analysis discussed in [48]. Three different sources of data, namely LIDAR, aerial imagery, and spaceborne imagery, were used for the retrieval of canopy cover by [69], among which the accuracy of the retrieval was highest with spaceborne WorldView2 data with an R² = 0.58, followed by aerial imagery with an R² = 0.50, and then LIDAR data with an R² = 0.33. The accuracies were low in comparison to the present work; however, the data concerned forest vegetation. The authors in [70] used the Chinese satellite Huan Jing (HJ1A/B) and Landsat-8 Operational Land Imager (OLI) images to retrieve the canopy cover in wheat fields. The authors initially generated simulations on the PROSAIL model and then the simulated data was used to train an Artificial Neural Network (ANN). The retrieval was performed for three years: 2013, 2014, and 2015, and compared with the ground data of that year with the overall RMSE = 7.17 and RRMSE = 9%. The RRMSE is somewhat higher in the present work than reported in [70]; there could be two possible reasons for this, the first one may be the non-optimal band selection of the VENµS satellite data for fvc retrieval and the other could be the equation that was used to convert the measurements of LAI into fvc. The solution to the first issue can be the identification of the optimal bands of the VENµS satellite data for fvc retrieval, for example using GPR band analysis [71], and for the second issue, the conversion equation can be tested with multiple-year canopy cover data. Although, in the present work, the RRMSE is a little higher than the Global Monitoring for Environment and Security (GMES) goal accuracy, i.e., 10%. We consider this fvc retrieval further as the aim of the work is to calibrate the AOS crop model for the localized application. The method of retrieving biophysical variables from multispectral satellite images have proven effective to train machine learning models with the PROSAIL simulated data [42]. However, other machine learning methods do not provide the uncertainty estimates with the mean value of predictions as in the case of GPR.

4.2. Parameters Identification

It can be seen that the initial uniform prior distribution has been transformed into a posterior distribution by integrating the observations into the AOS crop growth model. From the distributions, the parameter estimates (mean values) have been derived and the confidence intervals of the parameters estimated can be quantified. Figure 7 shows the marginal pdf of all the 15 crop model parameters subjected to the calibration of the model. It can be visualized from Figure 7 that the prior values of the crop model parameters differ from the mean values of the posterior distribution, especially in the case of CGC, WP, Kcb, HI0, Senscence, Tmin_up, fshape_b, GDD_lo CDC, and b_HI, which also signifies the importance of the Bayesian calibration. In [68], the calibration of the Aquacrop model was performed by integrating the MODIS LAI images for wheat, considering a similar set of parameters as that in the present work. The study carried out by [72] on the Bayesian calibration of the Aquacrop model also find WP, CGC, Kcb, and CDC important for the calibration, with the high errors reported by using the default parameter values. The authors only considered 10 model parameters for the local calibration of the model, unlike the present study that evaluated 15 crop model parameters for calibration, which identified the most sensitive crop model parameters to yield from previous work on global sensitivity analyses [63].

4.3. Calibration and Validation

The fvc time series simulated for the years 2018–2019, using the calibrated parameter values, was compared with the fvc time series of 2018–2019, generated using VENµS images. A good fit was observed in all the simulations (Figure 8), in agreement with the comments by [60]. As can be seen from Table 5, in the present study the linear correlation is in the range of 0.81 to 0.93, with the exception of 0.52 and 0.61 for the fields B062 and B069; because of the phenological shift in the fvc, these metrics are better than as reported in [68]. The AOS model parameter values obtained by the calibration were used for the validation and Figure 8 shows the validation on the years 2018–2019 for the fvc. The R² for the validation of the fvc for the years 2018–2019 also ranges from 0.69 to 0.86 for the different fields, while the retrieval of fvc from VENµS satellite images when compared to the ground-measured fvc data was 0.76 (Figure 4a).

As can be visualized from Figure 9a, the RRMSE for the simulated biomass is much higher than the usually acceptable range of 0–30%. This is the clear interpretation that the calibrated parameters did not work well for the estimation of the biomass. Although, there are uncertainties in the observed biomass and its processing, from the destructed samples collected to the oven dried samples; this could be one reason for the uncertainty accounted. While simulating yield, the RRMSE was 26.9%, which is fair and acceptable. The accuracy may be improved if the model is spatially applied to the entire field. In the present study, our focus was to find the optimal crop model parameter for the study area, so the calibration was performed on a few pixels. We are convinced that if the model is applied spatially to the study area, the accuracy would be higher than reported in the present work.

It should also be noted that the calibration was performed using fvc as a target variable, so the results for the yield simulations might be affected by other factors not taken into account in the calibration. In [65], it was argued that the estimating parameters on one response may not necessarily improve the predictions for a different response, but rather points at reducing the overall error of the model. Moreover, AOS is a new recent version of Aquacrop, coded on a different platform (MATLAB). Even if its performances have been checked [62], the newly coded versions of Aquacrop may still require refinement and extensive testing [73].

In general, simulations performed after calibration showed lower values of biomass and yield with respect to values obtained with the standard AOS parameters, decreasing the simulation bias with respect to the measured values. For the years 2018–2019, the grain yield simulated using the standard parameters was 15.4 t ha⁻¹, while the yield obtained with the calibrated parameters (average of the pixelwise parameters estimated for the previous year) was 11.9 t ha⁻¹, closer to the yield range usually recorded by their combination (2–10 t ha⁻¹).

The advantages of calibrating the model using a Bayesian approach over classical methods is that the parameter estimation is a posterior probability distribution that can be used to implement uncertainty analysis. This distribution can be summarized with the mean estimate along with confidence intervals unlike a single point estimate as in the classical methods. These approaches are becoming increasingly popular for parameter estimation of complex mathematical models, such as crop models, as it provides a coherent framework for dealing with uncertainty [16]. A comparative study of Bayesian calibration and optimization method-based calibration for the Aquacrop model utilizing UAV multispectral images shows the improved performance with the Bayesian method [72]. The main reason of the poor performance in the optimization method was that it aimed at minimizing the error between the measurement data and model output data, when inappropriate observations are chosen. On the other side, in the case of Bayesian approach, even if no sufficient dataset is available, one can easily observe this by inspecting the parameter estimation confidence [72].

All this considered, the significant improvements in the estimation of fvc and yield and the calibration workflow that integrates the VENµS satellite imagery and AOS offer encouraging results for the combination of remote sensing and crop modeling to improve yield estimations.

5. Conclusions

In this work, we have used VENµS satellite data to retrieve the fvc using state-of-the-art hybrid machine learning algorithms, specifically, GPR trained on PROSAIL model simulations of the canopy reflectance. The GPR algorithm was then applied to the VENµS satellite data time series to obtain the fvc data with their mean value of prediction and uncertainty and these were used to calibrate the AOS model in a Bayesian framework.

Bayesian inferences were preferred for the calibration as they transform the initial prior distribution to the posterior distribution from which the mean and median values can be computed, which reflects the optimal value of the parameter computed from its prior distribution. We implemented the Monte Carlo Markov chain-based DREAM extension, DREAM_(KZS), which involves three jumps: a parallel direction jump, snooker jump, and also a Kalman jump to speed up the convergence of the algorithm; we found that the algorithm is efficient in computing the parameter values in a time-constrained manner.

The results show that the AOS model gives good estimations of the canopy cover development on durum wheat. VENµS satellite images were useful to integrate the in-season fvc data for durum wheat, due to the revisit frequency of the satellite. Although the fvc provided good estimations of the canopy cover development, biomass and yield were overestimated in comparison to the ground data.

This study, therefore, concludes that the AOS crop model calibration improved the fvc simulated though it overestimated biomass and yield. Overestimation of the yield was not completely minimized, but it was reduced and thus it would be important to calibrate the model before yield estimation applications. The fvc derived from the VENµS satellite images was useful to perform such a calibration, specifically with Bayesian methods.