For the validation of the proposed method, we performed the kinematic POD for Sentinel-3A and Swarm-A satellites using ZD ambiguities resolution epoch by epoch to simulate the real-time situation. We also calculated the ambiguity–float solution for comparison. In this section, we begin with the analysis of ambiguity fixing rate and the Time to First Fix (TTFF). Afterwards, we assess the POD accuracy in terms of difference with post-processed reduced dynamic orbit products and SLR residuals. The phase residuals are also analyzed to further illustrate the impact of ZD AR on kinematic POD.
4.1. Ambiguity Fixing Results
In this subsection, the ambiguity fixing performance is evaluated in terms of the following aspects: ambiguity residuals, fixing rate, and TTFF. The ambiguity residuals are defined as the difference between the UPD-corrected ambiguity and its nearest integer. After subtracting the satellite and receiver UPDs, the float WL and NL ambiguities should be close to integer numbers. Therefore, the residuals distribution is a common quality index for the estimated UPD. For the purpose of illustration, the distribution of WL (left) and NL (right) residuals for day-of-year (DOY) 213 of 2018 is displayed in
Figure 3. Both the two histograms are symmetric, bell-shaped and concentrate to around zero. It can be found that over 90% WL and 93% NL ambiguity residuals are within 0.15 cycles, which further confirms the high reliability of WL and NL UPD correction.
Ambiguity fixing rate is defined as the percentage of epochs with both WL and NL ambiguities fixed in the whole period, and the TTFF refers to the time consuming for the first ambiguity to be successfully fixed [
50,
51].
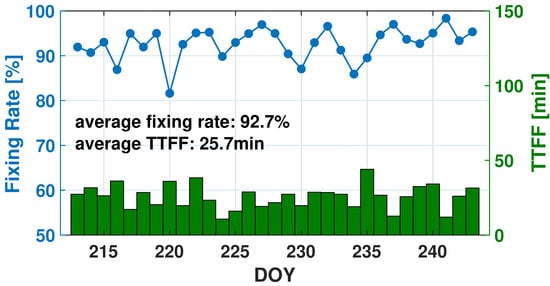
Figure 4 and
Figure 5 illustrate the daily ambiguity fixing rates and TTFF of Sentinel-3A and Swarm-A, respectively. It can be found that the fixing rates of Sentinel-3A are over 90% for most days with an average of 92.7%, while the mean TTFF is 25.7 min. The results are at a similar level compared with those of ground receivers [
23,
25]. Similar performance can also be observed for Swarm-A with an averaged fixing rate and TTFF of 90.7% and 29.7 min, respectively.
Generally, the majority of LEO missions are on altitudes of 300–1500 km. Below that level, a satellite’s orbit would rapidly decay due to the strong drag of the Earth’s atmosphere while the higher altitude is abandoned because of the impact of Van Allen Radiation Belts. As a result, the GNSS signals from GNSS satellites to LEO receivers won’t pass through the troposphere in most cases. The troposphere delay is thus ignored in the POD process. It contributes to an increase in the observation redundancy because of the reduction of estimated parameters, yielding a stronger solution strength. Moreover, considering that the LEO satellite’s orbital velocity is 3–7 km/s, the relative motion between the LEO and GNSS satellites would change much more rapidly than that of ground receivers, which leads to a relatively better geometry diversity for LEO POD. As a result, the multipath effects of LEO receivers would be mitigated effectively and the convergence time would be shortened in POD [
15]. However, as the side effect of the high dynamic, the signal passes (continuous tracking arcs) of LEO receivers are usually only around 15 min, which may hamper the NL ambiguity fixing [
25].
4.2. POD Results
In order to investigate the performance of proposed POD method, both the ambiguity–fixed solution and ambiguity–float solution are assessed from the following three aspects:
For the orbit difference comparison, the post-processed reduced dynamic orbit products from ESA are adopted as the reference orbits. This is because the kinematic orbits usually present inferior precisions than those of reduced dynamic orbits due to the absence of dynamical constraints [
30].
Figure 6 exhibits the orbit differences of Sentinel-3A satellite for ambiguity–fixed and ambiguity–float solutions in DOY 214, 2018, 12:00 a.m. to 6:00 a.m. The red dots refer to the ambiguity–fixed solution while the blue ones denote the ambiguity–float solution. For demonstration of the impact of GNSS satellites’ geometric distribution on LEO Kinematic POD, the visible satellite numbers, position dilution of precision (PDOP) values, and the latitude of LEO satellite ground tracks are also displayed. It can be found that the orbit errors of ambiguity–float solution in the along-track and radial components show dramatic and cyclic variations with a peak-to-peak value of approximately 20 cm. A similar phenomenon can also be observed in cross-track components, although it is less significant. Taking the LEO satellite’s latitude into consideration, we can recognize a potential correlation between the latitude change and periodic variation of orbit error: the LEO satellite shows inferior POD accuracy in high latitude while the POD accuracy is relatively better in low altitude. This may be attributed to the relatively less coverage of GNSS constellation in a high-latitude region (GPS satellites’ inclination is approximately
). As depicted in
Figure 6, the average PDOP value is 2.16 in middle and low latitudes (latitude <
) while it increases to 2.52 in high latitudes (latitude >
). In addition, due to the absence of dynamic constraint, kinematic orbit precisions are dominated by the observation quality. Thus, in case of observations’ sudden discontinuities and poor geometric distribution, the kinematic orbits usually present short-term systematic errors.
Compared with the float solution, the ambiguity–fixed solution provides a conspicuously smoother variation of the orbit errors. Once the undifferenced phase ambiguities are fixed to their integer values, the estimation would be strengthened immediately, which would offer additional geometric stiffness and ameliorate the orbit accuracy especially near the high latitude area. To mathematically demonstrate the impact of ambiguity fixing on the orbit errors’ cyclic variations, we calculated the Spearman’s correlation coefficients between latitudes of LEO ground tracks and the orbit errors. The statistics are listed in
Table 3. Spearman’s correlation coefficient is a statistical measure of the strength of a monotonic relationship between paired data [
52]. Unlike Pearson’s correlation, there is no requirement of the parameter’s normality, thus the Spearman’s correlation is more appropriate for the testing of latitudes and orbit errors. For Spearman’s correlation coefficient
, the closer
is to
indicates the stronger the monotonic relationship. In addition,
p-value refers to the significance test results. The smaller the
p-value is, the more confident we are to believe
. As shown in
Table 3, the
values of ambiguity–float solution are from 0.3 to 0.5 by magnitude, which indicate the moderate level monotonic relationships. After the ambiguity fixing, the
value for along-track orbit errors reduces to nearly zero with
p-value close to 1, strongly indicating the vanishing of the monotonic relationship. The cross-track orbit errors also show a smaller
value by magnitude. However, the radial orbit errors present even a worse
value compared with the ambiguity–float result, despite the fact that the ambiguity–fixed orbit error series achieves smaller variations. This is possibly attributed to the poor accuracy in radial components. Overall, the ambiguity fixing alleviates the correlation between orbit errors and latitudes i.e., the satellite geometric conditions. In practical cases, in order to obtain a maximum coverage of the Earth’s surface, the remote sensing satellites are usually injected into the polar or near-polar orbits. The superior performance of ambiguity–fixed solution thus indicates a high potential for improving diverse LEO-based geometric applications. Furthermore, an improvement on convergence time with ambiguity–fixed solution can also be recognized in
Figure 6, which is beneficial for the restart after the interrupted tracking in real-time POD.
Figure 7 shows the daily root mean square (RMS) values of real-time kinematic Sentinel-3A orbit differences for the ambiguity–fixed and ambiguity–float solutions. The along-track RMS values for ambiguity–float solution are around 4–6 cm while those for ambiguity–fixed are approximately 3–5 cm. Similar apparent improvement can also be noticed in cross-track and radial component for each day. The detailed statistics are summarized in
Table 4. It can be found that the RMS values of Sentinel-3A orbit for the ambiguity–fixed solution are 3.11, 2.19, and 3.59 cm in along-track, cross-track, and radial components, respectively, with an improvement of 30%, 28%, and 23% compared with the ambiguity–float solution. The 3D RMS value decreases from 7.15 cm to 5.23 cm by using ZD AR, which has met the precision requirement of most space missions in real-time situations.
Orbit differences of Swarm-A satellite in the same period are depicted in
Figure 8. Similar to Sentinel-3A, the mean PDOP values increase from 1.83 to 2.11 when the Swarm-A satellite passed the high-latitude areas (latitude >
). Again, the ambiguity–float solution shows evident and periodic variations over the orbital time scale with the peak-to-peak values about 12 cm. The orbit errors of the ambiguity–fixed solution, in the contrast, are remarkably smaller and more stable, particularly in the along-track and cross-track components. In addition, the Spearman’s correlation coefficients between latitudes of LEO ground tracks and the orbit errors for Swarm-A are also summarized. As presented in
Table 5, the
values for ambiguity–float orbit differences are 0.16 to 0.34, which implies the weak to moderate level monotonic relationships between orbit errors and latitudes. Due to the different orbit inclinations, Swarm-A shows opposite signs of
values to Sentinel-3A in the three components: the along-track and radial orbit errors show negative monotonic relationships with latitudes while that of cross-track is positive. In addition, the along-track orbit differences show the strongest correlation while the correlation in radial is the weakest. With the help of ZD AR, the
values can achieve 35–75% reductions and add up to around 0.1. Meanwhile, evident increments of
p-values are observed. In total, there is strong evidence to prove that the ambiguity fixing can strengthen the parameter estimation and alleviate the orbit errors caused by poor geometric distribution.
The daily RMS values of real-time kinematic Swarm-A orbit are presented in
Figure 9. It can be seen that the ambiguity–fixed solution presents a superior POD precision in three components compared with the ambiguity–float solution, with an improvement of around 25%. The 3D RMS value also reduces from 5.29 cm to 4.01 cm as a result of ambiguity resolution. It may be noticed that the Swarm-A orbits achieve 1–2 cm higher accuracy than those of Sentinel-3A. This is probably caused by the absence of Sentinel-3A’s precise attitude information and PCV values.
In addition to the comparison with post-processed reduced dynamic orbit, the ambiguity–fixed orbit and ambiguity–float orbit are also compared against SLR measurements. SLR can provide completely independent optical distance measurements between LEO satellite and ground stations with mm-to-cm-level precision. Thus, SLR residuals, i.e., differences between measured and modeled ranges, serve as a common figure of merit for validation of not only satellite orbits’ precision, but also accuracy [
53]. Both Sentinel-3A and Swarm-A are equipped with LRR, and their SLR observations are routinely provided by a worldwide network of the International Laser Ranging Service (ILRS) [
54]. However, the equations of motion for orbiting satellites refer to the satellite center of mass (CoM), so a rigorous correction is required to extrapolate the SLR measurements to the CoM. In this experiment, the CoM and LRR position information was from values recommended in [
30]. During the study period, the Sentinel-3A satellite was tracked by 17 ILRS stations and those of Swarm-A satellite was 19. Considering that the observation numbers of some ILRS stations are few (less than 50 normal points), two high-performance subsets of ILRS stations are selected for Sentinel-3A and Swarm-A orbit validation, respectively. The corresponding station IDs for Sentinel-3A are 1890, 7090, 7105, 7110, 7501, 7839, 7840, 7841, and 8834, while those for Swarm-A are 7090, 7105, 7237, 7501, 7821, 7825, 7827, 7839, and 7840. In addition, an empirical threshold of 0.2 m was used for deleting outliers in SLR validation.
SLR residuals for Sentinel-3A and Swarm-A are summarized in
Table 6 and
Table 7. In order to avoid the impact of station-specific ranging biases, the mean and standard deviation values of SLR residuals along with the number of normal points for individual ILRS stations are presented in the tables. For Sentinel-3A, all nine ILRS stations present notable smaller standard deviation values with an ambiguity–fixed solution w.r.t ambiguity–float solution. The reduction of standard deviation values are 0.4–1.8 cm, and the corresponding improvements are 8–40%. Statistics based on the full set of analyzed stations show that the mean and standard deviation values for ambiguity–float solution are −3.26 and 5.07 cm, while the ambiguity–fixed solution counterparts are −2.93 and 4.01 cm, with the standard deviation improvement of 21%.
Superior performances of ambiguity–fixed solution are also observed for Swarm-A SLR residuals. As presented in
Table 7, the ambiguity–fixed solution shows evident improvements in the standard deviation values for all the IRLS stations compared with the ambiguity–float solution. The improvements are most pronounced for station 7105, 7821, and 7827, whose standard deviation values reduce by 1–2 cm as a result of ambiguity fixing. The overall standard deviation value of ambiguity–fixed solution is 2.78 cm, with an improvement of 21% compared with the 3.53 cm of ambiguity–float solution. In addition, the overall mean value of SLR residuals also decreases by 0.7 cm in magnitude. The SLR residuals validate that ambiguity fixing could achieve not only higher precision, but also higher accuracy LEO orbit compared with ambiguity–float solution.
Apart from the assessment of LEO orbit precisions, the phase residuals are also analyzed to illustrate the impact of ZD AR on LEO POD. When the phase ambiguities are fixed to integer values, the observation equation and model precision will be notably strengthened. In this way, the integer phase ambiguities will be forcibly separated from other linear-correlated parameters and unmodeled errors, which used to be assimilated into float ambiguity estimates. As a consequence, the phase residuals will increase unavoidably. As exhibited in
Figure 10, the RMS values of Sentinel-3A phase residuals for the ambiguity–fixed solutions are 0.5–1.0 mm larger than those of the ambiguity–float solutions for each day. The analogous phenomenon can also be found in
Figure 11 for Swarm-A, the averaged RMS values of phase residuals are 6.33 mm for the ambiguity–float solution, while it is 6.79 mm for the ambiguity–fixed solution.