Deterministic Greedy Routing with Guaranteed Delivery in 3D Wireless Sensor Networks
Abstract
:1. Introduction



2. Construction of Unit Tetrahedron Cells

3. Routing at Internal UTCs: Face-Based Greedy Routing

4. Routing in 3D Sensor Network without Internal Holes
4.1. Theoretical Insights
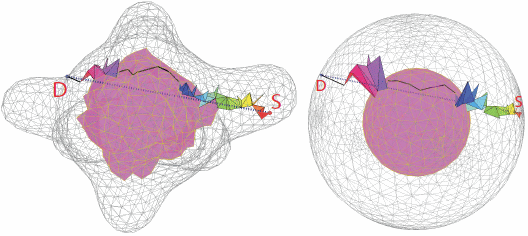
4.1.1. Volumetric Embedding
4.1.2. Volumetric Harmonic Function
4.1.3. Spherical Harmonic Function
4.2. Distributed Mapping Algorithm

4.2.1. Distributed Spherical Harmonic Map
4.2.2. Distributed Volumetric Harmonic Map
4.2.3. The Routing Algorithm
5. Routing in 3D Sensor Network with Internal Holes
5.1. 3D Sensor Networks with One Internal Hole
5.2. 3D Sensor Networks with Multiple Internal Holes

5.2.1. Network Segmentation and Mapping
5.2.2. Tunnel Routing


6. Applications and Simulations
6.1. Peer-to-Peer Greedy Routing
6.1.1. Stretch Factor
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | Model 7 | Model 8 | Average | |
|---|---|---|---|---|---|---|---|---|---|
| Ours | 1.63 | 1.63 | 1.66 | 1.61 | 1.62 | 1.44 | 1.69 | 1.72 | 1.62 |
| Random-walk [6] | 1.83 | 1.70 | 1.73 | 1.84 | 1.89 | 2.12 | 2.16 | 2.91 | 2.02 |

6.1.2. Load Distribution

6.2. Data Storage and Retrieval
6.2.1. Where to Store the Data
6.2.2. Route Data and Query
6.2.3. Networks with Multiple Internal Holes
6.2.4. Performance

7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bai, X.; Zhang, C.; Xuan, D.; Teng, J.; Jia, W. Low-connectivity and full-coverage three dimensional networks. In Proceedings of the MobiHOC, New Orleans, LA, USA, 18–21 May 2009; pp. 145–154.
- Bai, X.; Zhang, C.; Xuan, D.; Jia, W. Full-coverage and K-connectivity (K = 14, 6) three dimensional networks. In Proceedings of the INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 388–396.
- Liu, C.; Wu, J. Efficient geometric routing in three dimensional ad hoc networks. In Proceedings of INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 2751–2755.
- Kao, T.F.G.; Opatmy, J. Position-based routing on 3D geometric graphs in mobile ad hoc networks. In Proceedings of the 17th Canadian Conference on Computational Geometry, Windsor, ON, Canada, 10–12 August 2005; pp. 88–91.
- Opatrny, J.; Abdallah, A.; Fevens, T. Randomized 3D position-based routing algorithms for ad-hoc networks. In Proceedings of the Third Annual International Conference on Mobile and Ubiquitous Systems: Networking & Services, San Jose, CA, USA, July 2006; pp. 1–8.
- Flury, R.; Wattenhofer, R. Randomized 3D geographic routing. In Proceedings of the INFOCOM, Phoenix, AZ, USA, 13–18 April 2008; pp. 834–842.
- Li, F.; Chen, S.; Wang, Y.; Chen, J. Load balancing routing in three dimensional wireless networks. In Proceedings of the ICC, Beijing, China, 19–23 May 2008; pp. 3073–3077.
- Zhou, J.; Chen, Y.; Leong, B.; Sundar, P. Practical 3D geographic routing for wireless sensor networks. In Proceedings of the SenSys, Zurich, Switzerland, 3–5 November 2010; pp. 337–350.
- Pompili, D.; Melodia, T.; Akyildiz, I.F. Routing algorithms for delay-insensitive and delay-sensitive applications in underwater sensor networks. In Proceedings of the MobiCom, Los Angeles, CA, USA, 23–29 September 2006; pp. 298–309.
- Cheng, W.; Teymorian, A.Y.; Ma, L.; Cheng, X.; Lu, X.; Lu, Z. Underwater Localization in Sparse 3D Acoustic Sensor Networks. In Proceedings of the INFOCOM, Phoenix, AZ, USA, 13–18 April 2008; pp. 798–806.
- Allred, J.; Hasan, A.B.; Panichsakul, S.; Pisano, W.; Gray, P.; Huang, J.; Han, R.; Lawrence, D.; Mohseni, K. SensorFlock: An airborne wireless sensor network of micro-air vehicles. In Proceedings of the SenSys, Sydney, NSW, Australia, 6–9 November 2007; pp. 117–129.
- Cui, J.H.; Kong, J.; Gerla, M.; Zhou, S. Challenges: Building scalable mobile underwater wireless sensor networks for aquatic applications. IEEE Netw. 2006, 20, 12–18. [Google Scholar]
- Bose, P.; Morin, P.; Stojmenovic, I.; Urrutia, J. Routing with guaranteed delivery in ad hoc wireless networks. In Proceedings of the Third Workshop Discrete Algorithms and Methods for Mobile Computing and Communications, Seattle, WA, USA, 20 August 1999; pp. 48–55.
- Karp, B.; Kung, H. GPSR: Greedy perimeter stateless routing for wireless networks. In Proceedings of the MobiCom, Rome, Italy, 16–21 July 2001; pp. 1–12.
- Kranakis, E.; Singh, H.; Urrutia, J. Compass routing on geometric networks. In Proceedings of the Canadian Conference on Computational Geometry (CCCG), Vancouver, BC, Canada, 15–18 August 1999; pp. 51–54.
- Kuhn, F.; Wattenhofer, R.; Zhang, Y.; Zollinger, A. Geometric ad-hoc routing: Theory and practice. In Proceedings of the 22nd ACM Symposium on the Principles of Distributed Computing, Boston, MA, USA, 13–16 July 2003; pp. 63–72.
- Kuhn, F.; Wattenhofer, R.; Zollinger, A. Worst-case optimal and average-case efficient geometric ad-hoc routing. In Proceedings of the MobiHOC, Annapolis, MD, USA, 1–3 June 2003; pp. 267–278.
- Mitra, B.L.S.; Liskov, B. Path vector face routing: Geographic routing with local face information. In Proceedings of the ICNP, Boston, MA, USA, 6–9 November 2005; pp. 147–158.
- Frey, H.; Stojmenovic, I. On delivery guarantees of face and combined greedy-face routing in ad hoc and sensor networks. In Proceedings of the MobiCom, Los Angeles, CA, USA, 23–29 September 2006; pp. 390–401.
- Tan, G.; Bertier, M.; Kermarrec, A.M. Visibility-graph-based shortest-path geographic routing in sensor networks. In Proceedings of the INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1719–1727.
- Papadimitriou, C.; Ratajczak, D. On a conjecture related to geometric routing. Theor. Comput. Sci. 2005, 344, 3–14. [Google Scholar] [CrossRef]
- Angelini, P.; Frati, F.; Grilli, L. An algorithm to construct greedy drawings of triangulations. In Proceedings of the 16th International Symposium on Graph Drawing, Heraklion, Crete, Greece, 21–24 September 2008; pp. 26–37.
- Leighton, T.; Moitra, A. Some results on greedy embeddings in metric spaces. In Proceedings of the 49th IEEE Annual Symposium on Foundations of Computer Science, Philadelphia, PA, USA, 25–28 October 2008; pp. 337–346.
- Kleinberg, R. Geographic routing using hyperbolic space. In Proceedings of the INFOCOM, Anchorage, AK, USA, 6–12 May 2007; pp. 1902–1909.
- Cvetkovski, A.; Crovella, M. Hyperbolic embedding and routing for dynamic graphs. In Proceedings of the INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1647–1655.
- Sarkar, R.; Yin, X.; Gao, J.; Luo, F.; Gu, X.D. Greedy routing with guaranteed delivery using ricci flows. In Proceedings of the IPSN, San Francisco, CA, USA, 13–16 April 2009; pp. 121–132.
- Flury, R.; Pemmaraju, S.; Wattenhofer, R. Greedy routing with bounded stretch. In Proceedings of the INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1737–1745.
- Durocher, S.; Kirkpatrick, D.; Narayanan, L. On routing with guaranteed delivery in three-dimensional ad hoc wireless networks. In Proceedings of the International Conference on Distributed Computing and Networking, Kolkata, India, 5–8 January 2008; pp. 546–557.
- Zhou, H.; Xia, S.; Jin, M.; Wu, H. Localized algorithm for precise boundary detection in 3D wireless networks. In Proceedings of the ICDCS, Genoa, Italy, 21–25 July 2010; pp. 744–753.
- Zhong, Z.; He, T. MSP: Multi-sequence positioning of wireless sensor nodes. In Proceedings of the SenSys, Sydney, NSW, Australia, 6–9 November 2007; pp. 15–28.
- Giorgetti, G.; Gupta, S.; Manes, G. Wireless localization using self-organizing maps. In Proceedings of the IPSN, Cambridge, MA, USA, 25–27 April 2007; pp. 293–302.
- Li, L.; Kunz, T. Localization applying an efficient neural network mapping. In Proceedings of the Int’l Conference on Autonomic Computing and Communication Systems, Rome, Italy, 28–30 October 2007; pp. 1–9.
- Shang, Y.; Ruml, W.; Zhang, Y.; Fromherz, M.P.J. Localization from mere connectivity. In Proceedings of the MobiHOC, Annapolis, MD, USA, 1–3 June 2003; pp. 201–212.
- Shang, Y.; Ruml, W. Improved MDS-based localization. In Proceedings of the INFOCOM, Hong Kong, China, 7–11 March 2004; pp. 2640–2651.
- Gu, X.; Wang, Y.; Yau, S.T. Volumetric harmonic map. Commun. Inf. Syst. 2003, 3, 191–202. [Google Scholar] [CrossRef]
- Wan, S.; Ye, T.; Li, M.; Zhang, H.; Li, X. Efficient spherical parametrization using progressive optimization. In Proceedings of the First International Conference on Computational Visual Media, Beijing, China, 8–10 November 2012; pp. 170–177.
- Gu, X.; Wang, Y.; Chan, T.F.; Thompson, P.M.; Yau, S.T. Genus zero surface conformal mapping and its application to brain surface mapping. IEEE Tran. Med. Imaging 2004, 23, 949–958. [Google Scholar] [CrossRef] [PubMed]
- Alt, H.; Schwarzkopf, O. The voronoi diagram of curved objects. In Proceedings of the 11th Annual Symposium on Computational Geometry, Vancouver, BC, Canada, 5–7 June 1995; pp. 89–97.
- Li, J.; Jannotti, J.; de Couto, D.S.J.; Karger, D.R.; Morris, R. A scalable location service for geographic ad hoc routing. In Proceedings of the MobiCom, Boston, MA, USA, 6–11 August 2000; pp. 120–130.
- Li, X.; Kim, Y.J.; Govindan, R.; Hong, W. Multi-dimensional range queries in sensor networks. In Proceedings of the SenSys, Los Angeles, CA, USA, 5–7 November 2003; pp. 63–75.
- Yu-Chi, C.; I-Fang, S.; Chiang, L. Supporting multi-dimensional range query for sensor networks. In Proceedings of the ICDCS, Toronto, ON, Canada, 25–29 June 2007; pp. 35–35.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xia, S.; Yin, X.; Wu, H.; Jin, M.; Gu, X.D. Deterministic Greedy Routing with Guaranteed Delivery in 3D Wireless Sensor Networks. Axioms 2014, 3, 177-201. https://doi.org/10.3390/axioms3020177
Xia S, Yin X, Wu H, Jin M, Gu XD. Deterministic Greedy Routing with Guaranteed Delivery in 3D Wireless Sensor Networks. Axioms. 2014; 3(2):177-201. https://doi.org/10.3390/axioms3020177
Chicago/Turabian StyleXia, Su, Xiaotian Yin, Hongyi Wu, Miao Jin, and Xianfeng David Gu. 2014. "Deterministic Greedy Routing with Guaranteed Delivery in 3D Wireless Sensor Networks" Axioms 3, no. 2: 177-201. https://doi.org/10.3390/axioms3020177
APA StyleXia, S., Yin, X., Wu, H., Jin, M., & Gu, X. D. (2014). Deterministic Greedy Routing with Guaranteed Delivery in 3D Wireless Sensor Networks. Axioms, 3(2), 177-201. https://doi.org/10.3390/axioms3020177