iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1038/s42256-021-00427-7
Predicting myocardial infarction through retinal scans and minimal personal information | Nature Machine Intelligence
Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Predicting myocardial infarction through retinal scans and minimal personal information

Nature Machine Intelligence volume 4, pages 55–61 (2022)Cite this article

Subjects

Abstract

In ophthalmologic practice, retinal images are routinely obtained to diagnose and monitor primary eye diseases and systemic conditions affecting the eye, such as diabetic retinopathy. Recent studies have shown that biomarkers on retinal images, for example, retinal blood vessel density or tortuosity, are associated with cardiac function and may identify patients at risk of coronary artery disease. In this work we investigate the use of retinal images, alongside relevant patient metadata, to estimate left ventricular mass and left ventricular end-diastolic volume, and subsequently, predict incident myocardial infarction. We trained a multichannel variational autoencoder and a deep regressor model to estimate left ventricular mass (4.4 (–32.30, 41.1) g) and left ventricular end-diastolic volume (3.02 (–53.45, 59.49) ml) and predict risk of myocardial infarction (AUC = 0.80 ± 0.02, sensitivity = 0.74 ± 0.02, specificity = 0.71 ± 0.03) using just the retinal images and demographic data. Our results indicate that one could identify patients at high risk of future myocardial infarction from retinal imaging available in every optician and eye clinic.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: STROBE flow diagram for excluded participants.
Fig. 2: Overview of the proposed method.
Fig. 3: Estimation of LVM and LVEDV using manual and automatic annotations.
Fig. 4: Cross-validation results for MI prediction.
Fig. 5: ROC curves obtained from the external validation using AREDS dataset.

Similar content being viewed by others

Data availability

All UKB images and demographic data are available, with restrictions, from UKB. Researchers who use the UKB dataset must first complete the UKB online access management system application form. More information on accessing the UKB dataset can be found in this link: https://www.ukbiobank.ac.uk/enable-your-research/apply-for-access. The AREDS dataset (NCT00000145) is available in the dbGAP repository: https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000001.v3.p1.

Code availability

All algorithms used in this study were developed using libraries and scripts in PyTorch. The source code is publicly available at https://doi.org/10.5281/zenodo.5716142.

References

  1. Roth, G. A. et al. Global, regional, and national burden of cardiovascular diseases for 10 causes, 1990 to 2015. J. Am. College Cardiol. 70, 1–25 (2017).

    Article  Google Scholar 

  2. D’Agostino, R. B. et al. General cardiovascular risk profile for use in primary care. Circulation 117, 743–753 (2008).

    Article  Google Scholar 

  3. Wong, T. Y. et al. Retinal microvascular abnormalities and their relationship with hypertension, cardiovascular disease, and mortality. Survey Ophthalmol. 46 1, 59–80 (2001).

    Article  Google Scholar 

  4. McClintic, B. R., McClintic, J. I., Bisognano, J. D. & Block, R. C. The relationship between retinal microvascular abnormalities and coronary heart disease: a review. Am. J. Med. 123, 374–e1 (2010).

    Article  Google Scholar 

  5. Poplin, R. et al. Predicting cardiovascular risk factors from retinal fundus photographs using deep learning. Nat. Biomed. Eng. 2, 158–164 (2018).

    Article  Google Scholar 

  6. Cheung, C. et al. Quantitative and qualitative retinal microvascular characteristics and blood pressure. J. Hypertens. 27, 1380–1391 (2011).

    Article  Google Scholar 

  7. Tapp, R. J. et al. Associations of retinal microvascular diameters and tortuosity with blood pressure and arterial stiffness. Hypertension 74, 1383–1390 (2019).

    Article  Google Scholar 

  8. Gargeya, R. & Leng, T. Automated identification of diabetic retinopathy using deep learning. Ophthalmology 124, 962–969 (2017).

    Article  Google Scholar 

  9. Qummar, S. et al. A deep learning ensemble approach for diabetic retinopathy detection. IEEE Access 7, 150530–150539 (2019).

    Article  Google Scholar 

  10. Pickhardt, P. J. et al. Automated CT biomarkers for opportunistic prediction of future cardiovascular events and mortality in an asymptomatic screening population: a retrospective cohort study. Lancet Digit. Health 2, e192–e200 (2020).

    Article  Google Scholar 

  11. Petersen, S. E. et al. UK Biobank’s cardiovascular magnetic resonance protocol. J. Cardiovasc. Magn. Reson. 18, 1–7 (2015).

    Article  Google Scholar 

  12. MacGillivray, T. J. et al. Suitability of UK Biobank retinal images for automatic analysis of morphometric properties of the vasculature. PLoS ONE 10, 1–10 (2015).

    Article  Google Scholar 

  13. Fu, H. et al. Evaluation of retinal image quality assessment networks in different color-spaces. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2019 48–56 (Springer, 2019).

  14. Kaggle Diabetic Retinopathy Competition (Kaggle, accessed 19 January 2020); https://www.kaggle.com/c/diabetic-retinopathy-detection/data

  15. Zheng, Q., Delingette, H., Duchateau, N. & Ayache, N. 3D Consistent and robust segmentation of cardiac images by deep learning with spatial propagation. IEEE Trans. Med. Imaging 37, 2137–2148 (2018).

    Article  Google Scholar 

  16. Khaw, K.-T. et al. Association of hemoglobin A1c with cardiovascular disease and mortality in adults: the European prospective investigation into cancer in Norfolk. Annals Intern. Med. 141, 413–420 (2004).

    Article  Google Scholar 

  17. Levitan, E. et al. Hba1c measured in stored erythrocytes and mortality rate among middle-aged and older women. Diabetologia 51, 267–275 (2008).

    Article  Google Scholar 

  18. Gerstein, H. C. et al. The hemoglobin A1c level as a progressive risk factor for cardiovascular death, hospitalization for heart failure, or death in patients with chronic heart failure: an analysis of the Candesartan in heart failure: assessment of reduction in mortality and morbidity (CHARM) program. Arch. Intern. Med. 168, 1699–1704 (2008).

    Article  Google Scholar 

  19. Skali, H. et al. Cardiac structure and function across the glycemic spectrum in elderly men and women free of prevalent heart disease: the atherosclerosis risk in the community study. Circ. Heart Fail. 8, 448–454 (2015).

    Article  Google Scholar 

  20. Petersen, S. E. et al. Reference ranges for cardiac structure and function in cardiovascular magnetic resonance (CMR) imaging in Caucasians from the UK Biobank population cohort. J. Cardiovasc. Magn. Reson. 19, 18 (2017).

  21. Attar, R. et al. 3D Cardiac shape prediction with deep neural networks: simultaneous use of images and patient metadata. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2019 586–594 (Springer, 2019).

  22. The Age-Related Eye Disease Study Sytem Group et al.The Age-Related Eye Disease Study (AREDS): design implications AREDS report number 1. Control. Clin. Trials 20, 573–600 (1999).

    Article  Google Scholar 

  23. The Age-Related Eye Disease Study System Groupet al. The Age-Related Eye Disease Study system for classifying age-related macular degeneration from stereoscopic color fundus photographs: the Age-Related Eye Disease Study report number 6. Am. J. Ophthalmol. 132, 668–681 (2001).

    Article  Google Scholar 

  24. Antelmi, L., Ayache, N., Robert, P. & Lorenzi, M. Sparse multi-channel variational autoencoder for the joint analysis of heterogeneous data. In Proc. 36th International Conference on Machine Learning Vol. 97, 302–311 (PMLR, 2019).

  25. Kingma, D. P. & Welling, M. Auto-encoding variational Bayes. Proc. 2nd International Conference on Learning Representations (ICLR, 2014).

  26. Rezende, D. J., Mohamed, S. & Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. Proc. 31st International Conference on International Conference on Machine Learning, 32, 1278–1286 (ICML, 2014).

  27. Hotelling, H. Relations between two sets of variates. Biometrika 28, 321–377 (1936).

    Article  MATH  Google Scholar 

  28. Haufe, S. et al. On the interpretation of weight vectors of linear models in multivariate neuroimaging. NeuroImage 87, 96–110 (2014).

    Article  Google Scholar 

  29. Johnson, J. M. & Khoshgoftaar, T. M. Survey on deep learning with class imbalance. J. Big Data 6, 27 (2019).

    Article  Google Scholar 

  30. Suinesiaputra, A. et al. Fully-automated left ventricular mass and volume MRI analysis in the UK Biobank population cohort: evaluation of initial results. Int. J. Cardiovasc. Imag. 34, 281–291 (2018).

    Article  Google Scholar 

  31. Attar, R. et al. Quantitative CMR population imaging on 20,000 subjects of the UK Biobank imaging study: LV/RV quantification pipeline and its evaluation. Med. Image Anal. 56, 26–42 (2019).

    Article  Google Scholar 

  32. Keith, N. Some different types of essential hypertension: their course and prognosis. Am. J. Med. Sci. 268, 336–345 (1974).

    Article  Google Scholar 

  33. Bai, W. et al. Automated cardiovascular magnetic resonance image analysis with fully convolutional networks. J. Cardiovasc. Magn. Reson. 20, 65 (2018).

    Article  Google Scholar 

  34. Lin, K. et al. Automated assessment of left ventricular function and mass using heart deformation analysis: initial experience in 160 older adults. Acad. Radiol. 23, 321–325 (2016).

    Article  Google Scholar 

  35. Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B. & Hochreiter, S. GANs trained by a two time-scale update rule converge to a local Nash equilibrium. Proc. 31st International Conference on Neural Information Processing Systemsm 30, 6629–6640 (NeurIPS, 2017).

  36. Ferris, F. L. et al. Clinical classification of age-related macular degeneration. Ophthalmology 120, 844–851 (2013).

    Article  Google Scholar 

  37. Trinh, M., Kalloniatis, M. & Nivison-Smith, L. Vascular changes in intermediate age-related macular degeneration quantified using optical coherence tomography angiography. Transl. Vis. Sci. Technol. 8, 20 (2019).

    Article  Google Scholar 

  38. Grammer, T. B. et al. Cardiovascular risk algorithms in primary care: results from the detect study. Sci. Rep. 9, 1–12 (2019).

    Article  Google Scholar 

  39. Qureshi, W. T. et al. Impact of replacing the pooled cohort equation with other cardiovascular disease risk scores on atherosclerotic cardiovascular disease risk assessment (from the multi-ethnic study of atherosclerosis [mesa]). Am. J. Cardiol. 118, 691–696 (2016).

    Article  Google Scholar 

  40. Wallisch, C. et al. External validation of two framingham cardiovascular risk equations and the pooled cohort equations: a nationwide registry analysis. Int. J. Cardiol. 283, 165–170 (2019).

    Article  Google Scholar 

  41. Wallisch, C. et al. Re-estimation improved the performance of two framingham cardiovascular risk equations and the pooled cohort equations: a nationwide registry analysis. Sci. Rep. 10, 1–11 (2020).

    Google Scholar 

Download references

Acknowledgements

A.F.F. is supported by the Royal Academy of Engineering Chair in Emerging Technologies Scheme (grant no. CiET1819\19), the MedIAN Network (grant no. EP/N026993/1) funded by the Engineering and Physical Sciences Research Council (EPSRC). This work was also supported by the Intramural Research Program of National Library of Medicine and National Eye Institute, National Institutes of Health. This research was also supported by the European Union’s Horizon 2020 InSilc (grant no. 777119) and EPSRC TUSCA (grant no. EP/V04799X/1) programmes. E.D. acknowledges funding from the BHF grant FS/13/71/30378.

Author information

Authors and Affiliations

  1. Centre for Computational Imaging and Simulation Technologies in Biomedicine, School of Computing, University of Leeds, Leeds, UK

    Andres Diaz-Pinto, Nishant Ravikumar, Rahman Attar, Avan Suinesiaputra & Alejandro F. Frangi

  2. Leeds Institute for Cardiovascular and Metabolic Medicine, School of Medicine, University of Leeds, Leeds, UK

    Andres Diaz-Pinto, Nishant Ravikumar, Rahman Attar, Avan Suinesiaputra, Eylem Levelt, Erica Dall’Armellina, Chris P. Gale, Sven Plein & Alejandro F. Frangi

  3. Cixi Institute of Biomedical Engineering, Ningbo Institute of Materials, Technology and Engineering, Chinese Academy of Sciences, Ningbo, China

    Yitian Zhao

  4. Department of Cardiology, Leeds Teaching Hospitals NHS Trust, Leeds, UK

    Eylem Levelt, Erica Dall’Armellina, Chris P. Gale & Sven Plein

  5. Université Côte d’Azur, Inria Sophia Antipolis, Epione Project-Team, Biot, France

    Marco Lorenzi

  6. National Center for Biotechnology Information, National Library of Medicine, NIH, Bethesda, MD, USA

    Qingyu Chen & Zhiyong Lu

  7. Division of Epidemiology and Clinical Applications, National Eye Institute, NIH, Bethesda, MD, USA

    Tiarnan D. L. Keenan, Elvira Agrón & Emily Y. Chew

  8. Leeds Institute for Data Analytics, University of Leeds, Leeds, UK

    Chris P. Gale

  9. Department of Ophthalmology, York Teaching Hospital NHS Foundation Trust, York, UK

    Richard P. Gale

  10. Department of Health Sciences, University of York, York, UK

    Richard P. Gale

  11. Department of Cardiovascular Sciences, KU Leuven, Leuven, Belgium

    Alejandro F. Frangi

  12. Department of Electrical Engineering, KU Leuven, Leuven, Belgium

    Alejandro F. Frangi

  13. Alan Turing Institute, London, UK

    Alejandro F. Frangi

Authors
  1. Andres Diaz-Pinto
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nishant Ravikumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rahman Attar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Avan Suinesiaputra
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yitian Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Eylem Levelt
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Erica Dall’Armellina
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Marco Lorenzi
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Qingyu Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Tiarnan D. L. Keenan
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Elvira Agrón
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Emily Y. Chew
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Zhiyong Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Chris P. Gale
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Richard P. Gale
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. Sven Plein
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Alejandro F. Frangi
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.D.-P. designed and executed all experiments, conducted all subsequent statistical analyses, and drafted the manuscript. N.R. helped design the experiments, helped with the writing, data interpretation and made substantial revisions and edits of the draft manuscript. R.A. helped design the experiments, contributed to the data analysis and data cleaning. A.S. and Y.Z. contributed to the data analysis. E.L., E.D., C.P.G., R.P.G. and S.P. contributed to the analysis of retinal and cardiac magnetic resonance images and shaped the medical contribution of this work. M.L. contributed to the design and implementation of the mcVAE. Q.C., T.D.L.K., E.A., E.Y.C. and Z.L. contributed to the external validation of the proposed method. A.F.F. conceived the methodology, helped design the experiments and contributed to the writing. All authors contributed to the manuscript.

Corresponding author

Correspondence to Alejandro F. Frangi.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Machine Intelligence thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Variance Comparison.

Comparison of the joint latent space variance: Obtained distribution of the latent variables when using the mcVAE on only retinal images and both retina + CMR.

Extended Data Fig. 2 FID.

Distribution of the Frechet Inception Distance (FID) score: Obtained distribution of the FID score on the reconstructed CMR images.

Extended Data Fig. 3 LinearRegression Coefficients.

Coefficients obtained from the logistic regression applied to myocardial infarction prediction using the estimated LVM/LVEDV and demographic data. Chol stands for cholesterol, bmi for body mass index, ads for alcohol daily consumption status, sbpa and dbpa stand for systolic and diastolic blood pressure, respectively.

Extended Data Fig. 4 Bland-Altman plots for different retinal image sizes.

Bland-Altman plots, correlation plots, and ROC curves for estimated LVM/LVEDV and MI prediction using different retinal image sizes. The solid line represents the logistic regression, and the dotted line represents the identity line.

Extended Data Fig. 5 Bland-Altman plots for different dataset sizes.

Bland-Altman plots, correlation plots, and ROC curves for estimated LVM/LVEDV and MI prediction using different dataset sizes. The solid line represents the logistic regression, and the dotted line represents the identity line.

Extended Data Fig. 6 Bland-Altman plots for estimated LVM/LVEDV using only retinal images.

Estimation of LVM and LVEDV using retinal images only or demographic data only: Bland-Altman and correlation plots for estimated LVM/LVEDV using only retinal images (upper plots) and only demographic data (lower plots). The solid line represents the logistic regression, and the dotted line represents the identity line.

Extended Data Fig. 7 ROC curves for MI prediction using different demographic data.

ROC curves for MI prediction using different demographic data: An eye clinic (that is age, gender). Accuracy: 0.71 ± 0.01, Sensitivity: 0.74 ± 0.03, Specificity: 0.73 ± 0.06, Precision: 0.68 ± 0.03, and F1 Score: 0.71 ± 0.01. ROC curves for MI prediction using demographic data that may be available at a cardiology department (that is Age, Gender, BMI, Diastolic BP, Systolic BP, HbA1c scores, Glucose, Cholesterol, Smoking and Drinking status). Accuracy: 0.72 ± 0.03, Sensitivity: 0.74 ± 0.02, Specificity: 0.70 ± 0.05, Precision: 0.70 ± 0.05, and F1 Score: 0.72 ± 0.03. The solid line represents the logistic regression, and the dotted line represents the identity line.

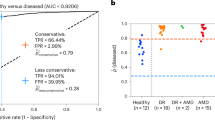
Extended Data Fig. 8 Coefficients and ROC curves for MI prediction obtained from the AREDS datasets.

Coefficients and ROC curves for MI prediction obtained from the AREDS datasets: (a) Coefficients obtained from the logistic regression applied to myocardial infarction prediction using the AREDS demographic data (sex, diastolic blood pressure (dbpa), systolic blood pressure (sbpa), smoking status (ss), body mass index (bmi) and age), and (b) ROC curve obtained for 10-fold cross-validation for MI predictions using only demographic data available in the AREDS dataset, and (c) ROC curve obtained for MI predictions using a logistic regression model trained on the UK Biobank and evaluated on the AREDS dataset. The solid line represents the logistic regression, and the dotted line represents the identity line.

Supplementary information

Supplementary Information

Supplementary Figs. 1–8, Tables 1–4 and Methods.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Diaz-Pinto, A., Ravikumar, N., Attar, R. et al. Predicting myocardial infarction through retinal scans and minimal personal information. Nat Mach Intell 4, 55–61 (2022). https://doi.org/10.1038/s42256-021-00427-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s42256-021-00427-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics