iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1023/A:1022197004856
Performance Evaluation and Policy Selection in Multiclass Networks | Discrete Event Dynamic Systems Skip to main content
Springer Nature Link
Log in

Performance Evaluation and Policy Selection in Multiclass Networks

  • Published:
Discrete Event Dynamic Systems Aims and scope Submit manuscript

Abstract

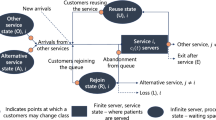
This paper concerns modeling and policy synthesis for regulation of multiclass queueing networks. A 2-parameter network model is introduced to allow independent modeling of variability and mean processing-rates, while maintaining simplicity of the model. Policy synthesis is based on consideration of more tractable workload models, and then translating a policy from this abstraction to the discrete network of interest. Translation is made possible through the use of safety-stocks that maintain feasibility of workload trajectories. This is a well-known approach in the queueing theory literature, and may be viewed as a generic approach to avoid deadlock in a discrete-event dynamical system. Simulation is used to evaluate a given policy, and to tune safety-stock levels. These simulations are accelerated through a variance reduction technique that incorporates stochastic approximation to tune the variance reduction. The search for appropriate safety-stock levels is coordinated through a cutting plane algorithm. Both the policy synthesis and the simulation acceleration rely heavily on the development of approximations to the value function through fluid model considerations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Asmussen, S. 1992. Queueing simulation in heavy traffic. Math. Operations Res. 17: 84–111.

    Google Scholar 

  • Atlason, J., Epelman, M. A., and Henderson, S. G. 2002. Combining simulation and cutting plane methods in service systems. In P. Reinig, editor, Proceedings of the 2002 National Science Foundation Design, Service and Manufacture Grantees and Research Conference.

  • BaÈuerle, N. 2000. Asymptotic optimality of tracking-policies in stochastic networks. Annals of Applied Probability 10: 1065–1083.

    Google Scholar 

  • Bell, S. L., and Williams, R. J. 1999. Dynamic scheduling of a system with two parallel servers: Asymptotic optimality of a continuous review threshold policy in heavy traffic. In Proceedings of the 38th Conference on Decision and Control. Pheonix, Arizona. pp. 1743–1748.

  • Benveniste, A., MeÂtivier, M., and Priouret, P. 1990. Adaptive Algorithms and Stochastic Approximations. Berlin: Springer-Verlag. Translated from the French by Stephen S. Wilson.

    Google Scholar 

  • Bertsimas, D., Paschalidis, I., and Tsitsiklis, J. N. 1994. Optimization of multiclass queueing networks: polyhedral and nonlinear characterizations of achievable performance. Ann. Appl. Probab. 4: 43–75.

    Google Scholar 

  • Borkar, V. S., and Meyn, S. P. 2000. The O.D.E. method for convergence of stochastic approximation and reinforcement learning. SIAM J. Control Optim. 38(2): 447–469 (electronic).

    Google Scholar 

  • Bramson, M., 1998. State space collapse with application to heavy traffic limits for multiclass queueing networks. Queueing Systems 30: 89–148.

    Google Scholar 

  • Bramson, M., and Dai, J. G. 2001. Heavy traffic limits for some queueing networks. Ann. Appl. Probab. 11(1): 49–90.

    Google Scholar 

  • Chen, H., and Mandelbaum, A. 1991. Stochastic discrete flow networks: diffusion approximations and bottlenecks. Ann. Probab. 19(4): 1463–1519.

    Google Scholar 

  • Chen, H., and Yao, D. D. 1993. Dynamic scheduling of a multiclass fluid network. Operations Research 41(6): 1104–1115.

    Google Scholar 

  • Chen, M., Pandit, C., and Meyn, S. P. 2001. In search of sensitivity in network optimization. Submitted for publication, and presented at the 11th INFORMS Applied Probability Society Conference.

  • Chen, R.-R., and Meyn, S. P. 1999. Value iteration and optimization of multiclass queueing networks. Queueing Systems Theory Appl. 32(1–3): 65–97.

    Google Scholar 

  • Courtois, P. J. 1977. Decomposability. New York: Academic Press.

    Google Scholar 

  • Dai, J. G., and Wang, Y. 1993. Nonexistence of Brownian models of certain multiclass queueing networks. Queueing Systems: Theory and Applications 13 (May): 41–46.

    Google Scholar 

  • Dembo, A., and Zeitouni, O. 1998. Large deviations techniques and applications. Second edition. New York: Springer-Verlag.

    Google Scholar 

  • Dubrawski, R. 2000. Myopic and far-sighted strategies for control of demand-driven networks. Master's thesis, Department of Electrical Engineering, UIUC, Urbana, Illinois, USA.

  • Dupuis, P., and Kushner, H. 2001. Numerical Methods for Stochastic Control Problems in Continuous Time. Applications of Mathematics, Vol. 24. New York: Springer Verlag.

    Google Scholar 

  • Feinberg, E. A., and Shwartz, A. 2001. Handbook of Markov Decision Processes. Boston: Kluwer Academic Publishers.

    Google Scholar 

  • Glynn, P. W., and Whitt, W. 1989. Indirect estimation via l = lw. Operations Research 37(1): 82–103.

    Google Scholar 

  • Harrison, J. M., and Van Mieghem, J. A. 1997. Dynamic control of Brownian networks: state space collapse and equivalent workload formulations. Ann. Appl. Probab. 7(3): 747–771.

    Google Scholar 

  • Harrison, J. M., and Wein, L. M. 1990. Scheduling networks of queues: Heavy traffic analysis of a two-station closed network. Operations Research 38(6): 1052–1064.

    Google Scholar 

  • Harrison, J. M. The BIGSTEP approach to flow management in stochastic processing networks. In F. P. Kelly, S. Zachary, and I. Ziedins, editors. Stochastic Networks Theory and Applications. Oxford, UK: Clarendon Press, 1996, pp. 57–89.

  • Henderson, S. G., and Meyn, S. P. 1997. Efficient simulation of multiclass queueing networks. In S. Andradottir, K. Healy, D. H. Withers, and B. L. Nelson, editors, Proceedings of the 1997 Winter Simulation Conference. Piscataway, NJ: IEEE, pp. 216–223.

  • Henderson, S. G., and Glynn, P. W. 2001. Approximating martingales for variance reduction in general discrete-event simulation. Working paper.

  • Henderson, S. G., and Glynn, P. W. 2002. Approximating martingales for variance reduction in Markov process simulation. Mathematics of Operations Research 27: 253–271.

    Google Scholar 

  • Henderson, S. G., and Meyn, S. P. 1999. Variance reduction for simulation in multiclass queueing networks. Submitted for publication.

  • Henderson, S. G., and Meyn, S. P. 2002. Identifying effective polices for multiclass networks. In P. Reining, editor, Proceedings of the 2002 National Science Foundation Design, Service and Manufacture Grantees and Research Conference.

  • Henderson, S. G. 1997. Variance Reduction Via an Approximating Markov Process. Ph.D. thesis, Department of Operations Research, Stanford University, Stanford, California, USA.

  • Hordijk, A., and Spieksma, F. 1992. On ergodicity and recurrence properties of a Markov chain with an application to an open Jackson network. Adv. in Appl. Probab. 24(2): 343–376.

    Google Scholar 

  • Kartashov, N. V. 1984. Criteria for uniform ergodicity and strong stability of Markov chains with a common phase space. Teor. Veroyatnost. i Mat. Statist. 151: 65–81.

    Google Scholar 

  • Kelley, J. E., Jr. 1960. The cutting-plane method for solving convex programs. Journal of the Society for Industrial and Applied Mathematics 8(4): 703–712.

    Google Scholar 

  • Kontoyiannis, I., and Meyn, S. P. 2001. Spectral theory and limit theorems for geometrically ergodic Markov processes. Ann. Appl. Probab. 2002. Presented at the 2001 INFORMS Applied Probability Conference, New York, July.

  • Kumar, P. R., and Meyn, S. P. 1996. Duality and linear programs for stability and performance analysis queueing networks and scheduling policies. IEEE Transactions on Automatic Control 41(1): 4–17.

    Google Scholar 

  • Kumar, S., and Kumar, P. R. 1994. Performance bounds for queueing networks and scheduling policies. IEEE Trans. Automat. Control AC-39 (August): 1600–1611.

  • Kumar, S., and Muthuraman, M. 2000. A numerical method for solving singular Brownian control problems. In Proceedings of the 39th Conference on Decision and Control.

  • Kushner, H. J. 2001. Heavy traffic analysis of controlled queueing and communication networks. Stochastic Modelling and Applied Probability. New York: Springer-Verlag.

    Google Scholar 

  • Kushner, H. J., and Yin, G. G. 1997. Stochastic Approximation Algorithms and Applications. New York: Springer-Verlag.

    Google Scholar 

  • Law, A. M., and Kelton, W. D. 2000. Simulation Modeling and Analysis. New York: McGraw-Hill, 3rd edition.

    Google Scholar 

  • Ljung, L., Pflug, G., and Walk, H. 1992. Stochastic approximation and optimization of random systems. Basel: BirkhaÈuser Verlag.

    Google Scholar 

  • Luo, X., and Bertsimas, D. 1998. A new algorithm for state-constrained separated continuous linear programs. SIAM J. Control Optim. 37: 177–210.

    Google Scholar 

  • Maglaras, C. 1997. Design of dynamic control policies for stochastic processing networks via fluid models. In Proceedings of the 38th Conference on Decision and Control, pp. 1208–1213.

  • Maglaras, C. 1999. Dynamic scheduling in multiclass queueing networks: Stability under discrete-review policies. Queueing Systems 31: 171–206.

    Google Scholar 

  • Maglaras, C. 2000. Discrete-review policies for scheduling stochastic networks: Trajectory tracking and fluidscale asymptotic optimality. Ann. Appl. Probab. 10: 897–929.

    Google Scholar 

  • Meyn, S. P. 2001. Columbia University lecture series on stochastic networks. Center for Applied Probability, Columbia University, New York, NY, July. http://black.csl.uiuc.edu/Ämeyn/pages/ColumbiaLectures.pdf.

  • Meyn, S. P. 1996. The policy iteration algorithm for average reward Markov decision processes with general state space. IEEE Trans. Automat. Control 42(12): 1663–1680, 1997. Also presented at the 35th IEEE Conference on Decision and Control, Kobe, Japan, December.

    Google Scholar 

  • Meyn, S. P. 1997. Stability and optimization of queueing networks and their fluid models. In Mathematics of Stochastic Manufacturing Systems (Williamsburg, VA, 1996). American Mathematical Society, Providence, RI, pp. 175–199.

  • Meyn, S. P. 2001. Sequencing and routing in multiclass queueing networks. Part I: Feedback regulation. SIAM J. Control Optim. 40(3): 741–776.

    Google Scholar 

  • Meyn, S. P. 2002. Sequencing and routing in multiclass queueing networks. Part II: Workload relaxations. SIAM J. Control Optim. To appear.

  • Meyn, S. P., and Down, D. G. 1994. Stability of generalized Jackson networks. Ann. Appl. Probab. 4: 124–148.

    Google Scholar 

  • Meyn, S. P., and Tweedie, R. L. 1993. Markov Chains and Stochastic Stability. London: Springer-Verlag, Available on-line at http://black.csl.uiuc.edu/Ämeyn.

    Google Scholar 

  • Morrison, J. R., and Kumar, P. R. 1999. New linear program performance bounds for queueing networks. Journal of Optimization Theory and Applications 100(3): 575–597.

    Google Scholar 

  • Nevel'son, M. B., and Has'minskiiÏ, R. Z. 1973. Stochastic Approximation and Recursive Estimation. American Mathematical Society, Providence, RI. Translated from the Russian by the Israel Program for Scientific Translations, Translations of Mathematical Monographs, Vol. 47.

  • Perkins, J. 1993. Control of Push and Pull Manufacturing Systems. Ph.D. thesis, University of Illinois, Urbana, IL, September. Technical report no. UILU-ENG–93–2237 (DC-155).

  • Reiman, M. I. 1984. Open queueing networks in heavy traffic. Mathematics of Operations Research 9: 441–458.

    Google Scholar 

  • Reiman, M. I. 1984. Some diffusion approximations with state space collapse. In Modelling and performance evaluation methodology (Paris, 1983). Berlin: Springer, pp. 209–240.

    Google Scholar 

  • Ross, S. M. 1996. Stochastic Processes. New York: Wiley, 2nd edition.

    Google Scholar 

  • Schwerer, E. 2001. A linear programming approach to the steady-state analysis of reflected Brownian motion. Stochastic Models 17: 341–368.

    Google Scholar 

  • Tadic, V., and Meyn, S. P. 2002. A stochastic approximation algorithm for variance reduction in simulation and reinforcement learning. In preparation.

  • Weiss, G. 2001. A simplex based algorithm to solve separated continuous linear programs. Technical Report, Department of Statistics The University of Haifa Mount Carmel 31905, Israel.

  • Whitt, W. 1989. Planning queueing simulations. Management Science 35: 1341–1366.

    Google Scholar 

  • Williams, R. J. 1998. Diffusion approximation for open multiclass queueing networks: sufficient conditions involving state space collapse. Queueing Systems 30(1–2): 27–88.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Operations Research and Industrial Engineering, Cornell University, Ithaca, NY, 14853, USA

    Shane G. Henderson

  2. Coordinated Science Laboratory and the University of Illinois, 1308 W. Main Street, Urbana, IL, 61801, USA

    Sean P. Meyn

  3. Department of Electrical and Electronic Engineering, The University of Melbourne, Parkville, Victoria, 3010, Australia

    Vladislav B. Tadić

Authors
  1. Shane G. Henderson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sean P. Meyn
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vladislav B. Tadić
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Henderson, S.G., Meyn, S.P. & Tadić, V.B. Performance Evaluation and Policy Selection in Multiclass Networks. Discrete Event Dynamic Systems 13, 149–189 (2003). https://doi.org/10.1023/A:1022197004856

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1022197004856

Keywords

Search

Navigation