A Hybrid Difference Scheme for a Second-Order Singularly Perturbed Reaction-Diffusion Problem with Non-smooth Data

Abstract

A singularly perturbed reaction-diffusion problem with a discontinuous source term is considered. In Miller et al. (J Appl Numer Math 35(4):323–337, 2000) the authors discussed problems that arises naturally in the context of models of simple semiconductor devices. Due to the discontinuity, interior layers appear in the solution. The problem is solved using a hybrid difference scheme on a Shishkin mesh. We prove that the method is second order convergent in the maximum norm, independently of the diffusion parameter. Numerical experiments support these theoretical results and indicate that the estimates are sharp.

Introduction

Singularly perturbed differential equations (SPDEs) appear in several branches of applied mathematics. Analytical and numerical treatment of these equations have drawn much attention of many researchers [1, 2]. In general, classical numerical methods fail to produce good approximations for these equations. Hence one has to go for non-classical methods. A good number of articles have been appearing in the past three decades on non-classical methods which cover mostly second order equations. Singularly perturbed second order problems are classified on the basis that how the order of the original differential equation is affected if one sets $\varepsilon =0$ [2]. Here $\varepsilon$ is a small positive parameter multiplying the highest derivative of the differential equation. We say that a singular perturbation problem (SPP) is of convection-diffusion type if the order of the differential equation is reduced by 1, whereas it is called reaction-diffusion type if the order is reduced by 2. In this paper the second type is considered. Various methods and applications are available in the literature in order to obtain numerical solution to SPDE of (1) subject to boundary conditions when $f(x)$ is discontinuous on $I_d$ [3–7]. In [8] the author examined singularly perturbed turning point problems exhibiting two exponential boundary layers using appropriate piecewise uniform Shishkin mesh and shown present method is layer resolving as well as parameter uniform convergent. A singularly perturbed two-point boundary-value problems (BVPs) for second-order ordinary differential equations (ODEs) arising in chemical reactor theory is proposed in [9] and to develop a numerical solution, an asymptotic approximation is incorporated into a suitable finite difference scheme. K. Mukherjee et al. [10] considered a singularly perturbed parabolic convection-diffusion one-dimensional problem and the proposed numerical scheme consists of classical backward-Euler method for the time discretization and a hybrid finite difference scheme for the spatial discretization, which provided second-order spatial accurate. The same author applied the similar technique to evaluate a class of singularly perturbed parabolic convection-diffusion problems with discontinuous convection coefficients in [11]. S. Natesan et al. [12] proposed a shooting method on parallel architecture for singularly perturbed two-point BVPs having less severe boundary layers. Two parameters singularly perturbed second-order ordinary differential equation with a discontinuous source term is presented in [13]. An appropriate piecewise uniform mesh is constructed to obtain parameter-uniform error bounds for the numerical approximation. Farrell et al. [3] examined a second order singularly perturbed reaction-diffusion equation in one dimension with discontinuity in the non-homogenous term and author derived first order convergence using fitted mesh method in shishkin mesh. In [4] the authors discussed parameter uniform schwartz method for the same type of problem on a non-standard piecewise uniform fitted mesh generating first order convergence in the maximum norm. Nevenka et al. [5] emphasized first order convergence for the similar type of problem by using pseudo spectral technique. In [6] the author considered singularly perturbed boundary value problem (SPBVP) of reaction-diffusion type with discontinuity at reaction co-efficient and non-homogenous term and obtained $O(Ch+\sqrt{\varepsilon })$ using boundary value technique. In [14], the author used a hybrid finite difference scheme for singularly perturbed convection-diffusion problem with discontinuous source term and obtained improved results. In [7] the author used a Galerkin finite element method uses on Shishkin and Bakhvalov-Shishkin-type of meshes is applied to a linear reaction-diffusion equation with discontinuous source term and shown to be convergent, uniformly in the perturbation parameter, of $O ((N^{-2}\,\, ln^{2} N))$ for the Shishkin type mesh and $O(N^{-2})$ for the Bakhvalov-Shishkin type mesh. Motivated by [3, 4, 6, 14] in the present paper we use hybrid difference scheme to improve the order of convergence for a second order SPBVP of reaction-diffusion type. The novel idea behind this problem is a jump at the interior layer and discontinuity in reaction co-efficient occurs at the same point (d). This is well balanced theory.

Through out this paper, C denotes a generic constant (sometime subscripted) that is independent of the singular perturbation parameter $\varepsilon$ and of $N$ the dimension of the discrete problem. Let us consider the singularly perturbed boundary value problem

$$\begin{aligned} \displaystyle&L_{\varepsilon } y(x) \equiv -\varepsilon y{^{\prime \prime }}(x)+b(x)y(x)=f(x),\quad x\in \varOmega ^-\cup \varOmega ^+ \end{aligned}$$

(1)

$$\begin{aligned} \displaystyle&y(0)=y_0, y(1)=y_1, \end{aligned}$$

(2)

where $b(x)\ge \beta >0$ is sufficiently smooth functions on $\bar{\varOmega }$ satisfying the following conditions, $\varOmega ^- = (0, d), \, \varOmega ^+ = (d, 1), \, \varOmega = (0, 1)$ and $\varepsilon$ is a small positive parameter. It is assumed that $f$ is sufficiently smooth on $\varOmega \setminus \{d\}$. Further it is assumed that $f(x)$ and its derivatives have jump discontinuity at the point $d \in \varOmega ,$ the solution $y$ of equations (1)–(2) does not necessarily have a continuous second order derivative at the point d. Thus $y \not \in C^2(\varOmega )$. But, $y \in C^1(\varOmega )$. It is convenient to introduce the notation for jump at $d$ for any function $y$ as $[y](d)=y(d+)-y(d-)$. These hypotheses guarantee the existence of a unique smooth solution $y$ of (1)–(2).

There is a vast literature dealing with numerical solution of reaction-diffusion problems with sufficiently smooth functions $b(x), f(x)$ see for instance [1, 2]. So far, problems of type (1)–(2) are considered in [2]. In [4] the authors analyzed parameter-uniform numerical methods for a singularly perturbed reaction-diffusion problem whose solution contain strong interior layers caused by a discontinuity and proved that the convergence is of order $O(N^{-1} \ln N).$

In this paper we will consider a hybrid difference scheme on a Shishkin mesh. The method is shown to be second order convergent $(O(N^{-1} \ln N))^2$. This method minimizes the error compared to the existing method in literature for the considered problem. Numerical examples are solved which coincides with the theoretical result.

Some Analytical Results

In this section, we derive a comparison principle for the following problem. Then using this principle, a stability result for the same problem is derived.

Theorem 1

The problem (1)–(2) has a solution $\;y \in C^1(\varOmega ) \cap C^2(\varOmega ^-\cup \varOmega ^+).\;$

Proof

The proof is by construction. Let $y_1(x), \, y_2(x)\;$ be particular solutions of the differential equations

$$\begin{aligned}&-\varepsilon y_1{^{\prime \prime }}(x) + b(x)y_1(x) = f(x), \quad x\in \varOmega ^-\ \text {and} \\&-\varepsilon y_2{^{\prime \prime }}(x) + b(x)y_2(x) = f(x), \quad x\in \varOmega ^+. \end{aligned}$$

Consider the function

$$\begin{aligned} y(x) = {\left\{ \begin{array}{ll} y_1(x) +(y(0)- y_1(0))\phi _1(x) +A\phi _2(x), \quad x\in \varOmega ^- \\ y_2(x) + B\phi _1(x)+(y(1)- y_2(1))\phi _2(x), \quad x\in \varOmega ^+ \end{array}\right. } \end{aligned}$$

where $\phi _1(x), \, \phi _2(x)\;$ are the solutions of the boundary value problems

$$\begin{aligned} -\varepsilon \phi _1{^{\prime \prime }}(x) + b(x) \phi _1(x)&= 0, \quad x\in \varOmega ,\quad \phi _1(0) = 1, \quad \phi _1(1) = 0\\ -\varepsilon \phi _2{^{\prime \prime }}(x) + b(x) \phi _2(x)&= 0, \quad x\in \varOmega ,\quad \phi _2(0) = 0, \quad \phi _2(1) = 1 \end{aligned}$$

and $A, B$ are constants to be chosen so that $y\in C^1(\varOmega ).\;$ Note that on the open interval $(0, 1), \, 0 < \phi _i < 1,~i = 1,~ 2.\;$ Thus $\phi _1,~\phi _2\;$ cannot have an internal maximum or minimum and hence

$$\begin{aligned} \phi _1{^\prime }(x)< 0, \quad \phi _2{^\prime }(x) > 0, \quad x\in (0, 1). \end{aligned}$$

We wish to choose the constants $A,~B$ so that $y \in C^1(\varOmega ).\;$ That is we impose

$$\begin{aligned} y(d^-) = y(d^+) \quad \text {and}\quad y'(d^-) = y'(d^+). \end{aligned}$$

For the constants $A,~B$ to exist we require

$$\begin{aligned} \begin{vmatrix} \phi _2(d)&- \phi _1(d) \\ \phi _2'(d)&-\phi _1{^\prime }(d) \end{vmatrix} \ne 0 \end{aligned}$$

This follows from observing that $\phi _2{^\prime }(d)\phi _1(d)- \phi _2(d)\phi _1{^\prime }(d) > 0.$ $\square$

Then $L_\varepsilon$ satisfies the following maximum principle on $\; \overline{\varOmega }. \; L_\varepsilon$ in (1)–(2) is solved by Shishkin mesh in [1].

Theorem 2

(Maximum Principle) Suppose that a function $y(x) \in {\mathcal C}^0(\overline{\varOmega }) \cap C^1(\varOmega ) \cap C^2(\varOmega ^-\cup \varOmega ^+)$ satisfies,

$$\begin{aligned} y(0)&\ge 0,\quad y(1)\ge 0, \\ L_\varepsilon y(x) \,&\ge 0, \quad \forall ~~ x \in \varOmega ^-\cup \varOmega ^+,\\ \left[ {y} \right] (d)&= 0, \quad \left[ {y{^\prime }} \right] (d) \le 0, \\ Then, ~~ y(x)&\ge 0,\quad \forall ~~ x \in \overline{\varOmega }. \end{aligned}$$

Proof

Let p be any point at which y attains its maximum value in $\bar{\varOmega }$. If $y(p)\ge 0,$ there is nothing to prove. Suppose that $y(p)<0,$ then the proof is completed by showing that this leads to contradiction. With the above assumption on the boundary values, either $p \in (\varOmega ^- \cup \varOmega ^+)$ or p=d. In the first case $y{^{\prime \prime }}(p)\ge 0$ and so

$$\begin{aligned} L_{\varepsilon } y(p) = -\varepsilon y{^{\prime \prime }}(p)+b(p)y(p) < 0 \end{aligned}$$

which is false. In the second case the argument depends on whether or not $y$ is differentiable at d. If $y{^\prime }(d)$ does not exist, then $[y{^\prime }](d) \ne 0$ and because $y{^\prime }(d^-) \le 0, y{^\prime }(d^+)\ge 0$ it is clear that $[y{^\prime }](d)>0,$ which is a contradiction. On the other hand if y is differentiable at d, then $y{^\prime }(d)=0$ and $y \in C^1(\varOmega )$. Recalling that $y(d)<0$ it follows that there exists a neighborhood $N_h=(d-h,d)$ such that $y(x)<0$ for all $x\in N_h$. Now choose a point $x_1 \ne d, x_1 \in N_h$ such that $y(x_1)>y(d).$ It follows from the mean values theorem that, for some $x_2 \in N_h$,

$$\begin{aligned} y{^\prime }(x_2)=\dfrac{y(d)-y(x_1)}{d-x_1}<0 \end{aligned}$$

and also that for some $x_3 \in N_h$,

$$\begin{aligned} y''(x_3)=\dfrac{y{^\prime }(d)-y{^\prime }(x_2)}{d-x_2}=\dfrac{-y{^\prime }(x_2)}{d-x_2}>0 \end{aligned}$$

Note also that $y(x_3)<0,$ since $x_3 \in N_h.$ Thus

$$\begin{aligned} L_{\varepsilon }y(x_3)=-\varepsilon y{^{\prime \prime }}(x_3)+b(x_3)y(x_3)<0 \end{aligned}$$

which is the required contradiction. Hence the proof of the theorem. $\square$

An immediate consequence of the maximum principle is the following stability result.

Theorem 3

(Stability Result) Let $y (x)$ be a solution $(P_\varepsilon ) ,$ then

$$\begin{aligned} \parallel y (x) \parallel _{\overline{\varOmega }} ~ \le ~ max \left\{ \mid y(0) \mid ,\mid y(1) \mid , \dfrac{1}{\beta } \parallel f \parallel _{\varOmega ^-\cup \varOmega ^+} \right\} \end{aligned}$$

Proof

Put $\varPsi _{\pm }(x) = M \pm y(x),$

where $M=max\left\{ \mid y(0) \mid ,\mid y(1) \mid ,\dfrac{1}{\beta } \parallel f \parallel _{\varOmega ^-\cup \varOmega ^+} \right\}$.

Then clearly $\varPsi _{\pm }(0) \ge 0, \varPsi _{\pm }(1) \ge 0$ and for each $x \in (\varOmega ^-\cup \varOmega ^+)$

$$\begin{aligned} L_{\varepsilon } \varPsi _{\pm } (x) = b(x)M \pm L_{\varepsilon }y (x) \ge \beta M \pm f(x) \ge 0 \end{aligned}$$

Furthermore, since $y ~\text {in}~ C^1(\varOmega )$

$$\begin{aligned}{}[\varPsi _{\pm }](d) = \pm [y](d)=0 ~\text {and}~ [\varPsi {^\prime }_{\pm }](d) = \pm [y{^\prime }](d)=0 \end{aligned}$$

It follows from the maximum principle that $\varPsi _{\pm }(x) \ge 0$ for all $x \in \overline{\varOmega }$, which leads at once to the desired bound on $y(x).$

An immediate consequence of this result is that the solution $y(x)$ of $(P_{\varepsilon })$ is unique. To establish the parameter-robust properties of the numerical methods involved in this paper, the following decomposition of $y(x)$ into smooth $v_{\varepsilon }(x)$ and singular $w_{\varepsilon }(x)$ components are required. The smooth component $v_{\varepsilon }(x)$ is defined as the solution of

$$\begin{aligned}&L_{\varepsilon } v_{\varepsilon } (x)= f(x) \quad x ~ \in ~ (\varOmega ^- \cup \varOmega ^+) \\&v_{\varepsilon }(0)=\dfrac{f(0)}{b(0)},~v_{\varepsilon }(d^-)=\dfrac{f(d^-)}{b(d)},~v_{\varepsilon }(d^+)=\dfrac{f(d^+)}{b(d)},~v_{\varepsilon }(1)=\dfrac{f(1)}{b(1)} \end{aligned}$$

and the singular component $w_{\varepsilon }(x)$ is given by

$$\begin{aligned} L_{\varepsilon } w_{\varepsilon }(x)&= 0 \quad x ~ \in ~ (\varOmega ^- \cup \varOmega ^+) \\ {[w_{\varepsilon }(d)]}&= -[v_{\varepsilon }(d)], [w{^\prime }_{\varepsilon }(d)] = -[v{^\prime }_{\varepsilon }(d)] \\ w_{\varepsilon }(0)&= y(0) - v_{\varepsilon }(0), w_{\varepsilon }(1) = y(1) - v_{\varepsilon }(1) \end{aligned}$$

As in Theorem 1, the singular component $w_{\varepsilon }(x)$ is well defined and is given by

$$\begin{aligned} w_{\varepsilon } (x) = {\left\{ \begin{array}{ll} w_{\varepsilon }(0) \psi _1(x) + A_1 \psi _2(x), \quad x \in \varOmega ^- \\ B_1 \psi _3(x) + w_{\varepsilon }(1)\psi _4(x), \quad x \in \varOmega ^+ \end{array}\right. } \end{aligned}$$

where $\psi _i(x),i=1,2,3,4$ are the solutions of the boundary value problems

$$\begin{aligned} -\varepsilon \psi _1{^{\prime \prime }} + b(x) \psi _1 = 0,~x \in \varOmega ^-, ~~ \psi _1(0)=1,\psi _1(d)=0 \\ -\varepsilon \psi _2{^{\prime \prime }} + b(x) \psi _2 = 0,~x \in \varOmega ^-, ~~ \psi _2(0)=0,\psi _2(d)=1 \\ -\varepsilon \psi _3{^{\prime \prime }} + b(x) \psi _3 = 0,~x \in \varOmega ^+, ~~ \psi _3(d)=1,\psi _3(1)=0 \\ -\varepsilon \psi _4{^{\prime \prime }} + b(x) \psi _4 = 0,~x \in \varOmega ^+, ~~ \psi _4(d)=0,\psi _4(1)=1 \\ \end{aligned}$$

and $A_1,B_1$ are constants to be chosen so that the jump conditions at $x=d$ are satisfied. One can easily show that $|A_1|,|B_1| \le C$, where C is a constant independent of $\varepsilon$.

Using stability result, theorem 2 and the technique used in [3] the following theorem can be proved.

Theorem 4

For each integer k, satisfies $0 \le k \le 4,$ the smooth $v_\varepsilon$ and singular $w_\varepsilon$ satisfy the bounds.

$$\begin{aligned} \mid v^{(k)}_\varepsilon (x)\mid&\le {\left\{ \begin{array}{ll} C(1 + \varepsilon ^{1-k/2} e_1(x)), \qquad x \in \varOmega ^-\\ C(1 + \varepsilon ^{1-k/2} e_2(x)), \qquad x \in \varOmega ^+ \end{array}\right. }\\ \mid w^{(k)}_\varepsilon (x)\mid&\le {\left\{ \begin{array}{ll} C(\varepsilon ^{-k/2} e_1(x)), \qquad x \in \varOmega ^-\\ C(\varepsilon ^{-k/2} e_2(x)), \qquad x \in \varOmega ^+ \end{array}\right. } \end{aligned}$$

where C is a constant independent of $\varepsilon$ and

$$\begin{aligned} e_1(x)=e^{-x\sqrt{(\beta /\varepsilon )}} + e^{-(d-x) \sqrt{(\beta /\varepsilon )}},~~ e_2(x)=e^{-(x-d)\sqrt{(\beta /\varepsilon )}} + e^{-(1-x) \sqrt{(\beta /\varepsilon )}} \end{aligned}$$

$\square$

Note that $v_{\varepsilon }, w_{\varepsilon } \notin C^0(\overline{\varOmega }),$ but $y = v_{\varepsilon }+w_{\varepsilon } \in C^1(\overline{\varOmega })$

Mesh and Scheme

On $\varOmega$ a piecewise uniform mesh of N mesh intervals is constructed as follows. The domain $\; \varOmega ^-\;$ is subdivided into the three subintervals. $[0, \tau _1], [\tau _1, d-\tau _1]~\text {and}~[d-\tau _1, d]$ for some $\;\tau _1\;$ that satisfies $\; 0 < \tau _1 \le \dfrac{d}{4}.\;$ On $[0, \tau _1]~ \text {and} ~[d-\tau _1, d]$ an uniform mesh with $\;\dfrac{N}{8}\;$ mesh intervals is placed, while on $\;[\tau _1, d-\tau _1]\;$ has a uniform mesh with $\;\dfrac{N}{4}\;$ mesh intervals. The subintervals $\;[d,d+\tau _2], [d+\tau _2, 1-\tau _2], \, [1-\tau _2, 1]\;$ of $\;\varOmega ^+\;$ are treated analogously for some $\;\tau _2\;$ satisfying $\; 0 < \tau _2 \le \dfrac{1-d}{4}.\;$ The interior points of the mesh are denoted by

$$\begin{aligned} \varOmega _\epsilon ^N = \Big \{ x_i: 1\le i \le \frac{N}{2} -1\Big \} \cup \Big \{ x_i: \frac{N}{2}+1\le i \le N -1\Big \}. \end{aligned}$$

Clearly $\;x_{N/2}=d \;$ and $\;\overline{\varOmega }_\varepsilon ^N=\{x_i\}_0^N.\;$ Note that this mesh is a uniform mesh when $\;\tau _1 =\dfrac{d}{4}\;$ and $\;\tau _2 =\frac{1-d}{4}.\;$ It is fitted to the SPP (1)–(2) by choosing $\;\tau _1\;$ and $\; \tau _2\;$to be the following functions of N and $\;\varepsilon \;$

$$\begin{aligned} \tau _1 = \min \left\{ \dfrac{d}{4}, 2\sqrt{\varepsilon /\beta } \ln N \right\} \qquad \end{aligned}$$

and

$$\begin{aligned} \tau _2 = \min \left\{ \dfrac{1-d}{4}, 2\sqrt{\varepsilon /\beta } \ln N \right\} . \end{aligned}$$

On the piecewise-uniform mesh $\;\overline{\varOmega }_\varepsilon ^N\;$ a standard centered finite difference operator is used. Then the fitted mesh method for (1)–(2) is

$$\begin{aligned} \displaystyle&L_c^N y_i \equiv -\varepsilon \delta ^2 y_{i}+b(x_i) y_{i}=f(x_i),\quad \forall \quad x_i~ \in ~ \varOmega _\varepsilon ^N \setminus \{d\},\end{aligned}$$

(3)

$$\begin{aligned} \displaystyle&y(0)=y_0, \qquad y(1)=y_N, \end{aligned}$$

(4)

where

$$\begin{aligned} \delta ^2 y_i=\left( \dfrac{y_{i+1}-y_i}{x_{i+1}-x_i}-\dfrac{y_i-y_{i-1}}{x_i-x_{i-1}}\right) \dfrac{2}{x_{i+1}-x_{i-1}}, \end{aligned}$$

At the point $x_{N/2}=d$ we shall use the hybrid difference operator $L_t^N;$

$$\begin{aligned} L_{t}^N y_{N/2}=\dfrac{-y_{N/2+2}+4y_{N/2+1}-3y_{N/2}}{2h}-\dfrac{y_{N/2-2}-4y_{N/2-1}+3y_{N/2}}{2h}=0 \end{aligned}$$

$$\begin{aligned} L^N y_i&= {\left\{ \begin{array}{ll} L_c^N y_i, \quad i \ne N/2 \\ L_{t}^N y_i, \quad i=N/2, \end{array}\right. }\end{aligned}$$

(5)

$$\begin{aligned} y(0)&= y_0, \qquad y(1)=y_N. \end{aligned}$$

(6)

Analysis of the Method

The matrix associated with (5)–(6) is not an M-matrix. We transform the equation so that the new equation do have a monotonicity property. From equation (3)–(4) we can get

$$\begin{aligned} y_{N/2-2}=\Big (f_{N/2-1}-b_{N/2-1} y_{N/2-1}-\dfrac{\varepsilon }{h}\dfrac{y_{N/2}-y_{N/2-1}}{h} +\dfrac{\varepsilon }{h^2}y_{N/2-1}\Big )\dfrac{h^2}{\varepsilon }\\ y_{N/2+2}=\Big (f_{N/2+1}-b_{N/2+1}y_{N/2+1}+\dfrac{\varepsilon }{h}\dfrac{y_{N/2+1}-y_{N/2}}{h} +\dfrac{\varepsilon }{h^2}y_{N/2+1}\Big )\dfrac{h^2}{\varepsilon } \end{aligned}$$

Inserting the expressions for $y_{N/2+2}$ and $y_{N/2-2}$ in $L_{t}^N$ gives

$$\begin{aligned} L_{T}^N y_{N/2}&= \Big ((2+\dfrac{h^2}{\varepsilon }b_{N/2+1})y_{N/2+1}-4 y_{N/2} +(2+\dfrac{h^2}{\varepsilon }b_{N/2-1}) y_{N/2-1}\Big )\dfrac{1}{2h}\\&= \Big (f_{N/2+1}+f_{N/2-1}\Big )\dfrac{h}{2\varepsilon } \end{aligned}$$

Now clearly we have a system of equations

$$\begin{aligned}&L_H^N y_i = {\left\{ \begin{array}{ll} L_c^N y_i \quad \text {for} \quad i \ne N/2 \\ L_{T}^N y_i \quad \text {for} \quad i = N/2, \end{array}\right. }\end{aligned}$$

(7)

$$\begin{aligned}&y_0 = y(0), \quad y_N = y(1) \end{aligned}$$

(8)

As in this case of continuous problem, it is easy to prove the discrete maximum principle and discrete stability result for the discrete problem of (7)–(8).

To bound the nodal error $|y(x_i) - y_i|,$ our method is similar to that of [15]. We define smooth $\bar{v}_i$ and singular $\bar{w}_{L,i}, \bar{w}_{R,i}$ components as follows.

$$\begin{aligned} \bar{v}_i={\left\{ \begin{array}{ll} v_{L,i} \quad i = N/8,\ldots ,d-N/8,\\ v_{R,i} \quad i= d+N/8,\ldots ,1-N/8, \end{array}\right. } \end{aligned}$$

which approximate $v(x_i)$ respectively to the left and to the right of the point of discontinuity x=d. The singular component $\bar{w}_{L,i} ~\text {and}~ \bar{w}_{R,i}$ such that,

$$\begin{aligned}&\bar{w}_{L,i} =&{\left\{ \begin{array}{ll} w_{L,1},\quad for \quad i = 0,\ldots ,N/8 \\ w_{L,2},\quad for \quad i = d-N/8,\ldots ,d-1 \end{array}\right. } \text {and} \\&\bar{w}_{R,i} =&{\left\{ \begin{array}{ll} w_{R,1},\quad for \quad i = d+1,\ldots ,d+N/8 \\ w_{R,2},\quad for \quad i = 1-N/8,\ldots ,1. \\ \end{array}\right. } \end{aligned}$$

Then we construct mesh function $\bar{w}_{L,i}$ and $\bar{w}_{R,i}$ (to approximate $w(x_i)$ on either side of $x=d$) so that the amplitude of the jump $\bar{w}_{R,i} (d) - \bar{w}_{L,i}(d)$ is determined by the size of the jump $|[v](d)|.$ Also $\bar{w}_{L,i}$ and $\bar{w}_{R,i}$ are sufficiently small away from the interior layer region. Using these mesh functions the nodal error $|y(x_i) - y_i|$ is then bounded separately outside and inside the layer. Define the mesh function $w_{L,1}, w_{L,2}, w_{R,1} \text {and}~w_{R,2}$ to the solutions of the following system of finite difference equations

$$\begin{aligned} \displaystyle&L_H^N \bar{w}_{L,i} = 0, \quad for \, i = 0,\ldots ,N/8,\quad and \quad for \quad ~ i = d-N/8,\ldots ,d-1 \\ \displaystyle&L_H^N \bar{w}_{R,i} = 0, \quad for \, i = d+1,\ldots ,d+N/8, \quad and \quad for \quad ~ i = 1-N/8,\ldots ,1, \\ \displaystyle&v_{L,N/2}+ \bar{w}_{L,N/2} = v_{R,N/2} + \bar{w}_{R,N/2} , \\ \displaystyle&L_{t}^N v_{L,N/2} + L_{t}^N \bar{w}_{L,N/2} = L_{t}^N v_{R,N/2} + L_{t}^N \bar{w}_{R,N/2}. \end{aligned}$$

Note that we can define $y_i$ to be

$$\begin{aligned} y_i = {\left\{ \begin{array}{ll} v_{L,i} + \bar{w}_{L,i}, \qquad for ~ i = 0,\ldots ,N/8,~\text {and}~i = d-N/8,\ldots ,d-1 \\ v_{L,i} + \bar{w}_{L,i} = v_{R,i} + \bar{w}_{R,i}, \quad for ~ i = d, \\ v_{R,i} + \bar{w}_{R,i}, \qquad for ~ i = d+1,\ldots ,d+N/8,\quad \text {and}\quad i = 1-N/8,\ldots ,1, \end{array}\right. } \end{aligned}$$

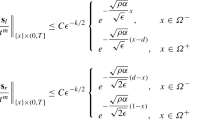
For smooth function based on the [2, 16] we can obtain the result as $|v(x_i) - v_i| \le C N^{-2}$. For the singular component using the arguments in [2]

$$\begin{aligned}&| w(x_i) - \bar{w}_{L,i} | \le C (N^{-1}\ln N)^2, \quad i=0,1,\ldots ,N/8, \\&| w(x_i) - \bar{w}_{R,i} | \le C (N^{-1}\ln N)^2,\quad i = 1-N/8,\ldots ,N. \end{aligned}$$

Based on the arguments [2, 16] from the arguments in [2] we can prove the following result except at x =d

$$\begin{aligned} |y(x_i) - y_i| \le C (N^{-1}\ln N)^2, \quad \forall ~ x_i \in \overline{\varOmega }\setminus \{d\} \end{aligned}$$

(9)

At the mesh point $x_{N/2}=d$

$$\begin{aligned} \mid L_H^N y_{N/2} - L_{\varepsilon } y_{N/2} \mid&= \mid L_H^N y_{N/2} - \big (f_{N/2+1} + f_{N/2-1}\big )\dfrac{h}{2 \varepsilon } \mid \\&= \mid L_{\varUpsilon }^N y_{N/2} - \big (f_{N/2+1} + f_{N/2-1}\big )\dfrac{h}{2 \varepsilon } \mid \\&\le \mid \dfrac{y_{N/2-2} - 4y_{N/2-1} + 3y_{N/2}}{2h} \mid \\&+ \mid \dfrac{-y_{N/2+2} + 4y_{N/2+1} - 3y_{N/2}}{2h} \mid \\&+ C \mid L y_{N/2-1} - L^N_c y^N_{N/2-1} \mid + C \mid L y_{N/2+1} - L^N_c y^N_{N/2+1} \mid \\ \mid L_H^N y_{N/2} - L_{\varepsilon } y_{N/2} \mid&\le \dfrac{Ch^2}{\varepsilon ^{3/2}} = C\dfrac{\tau ^2}{\varepsilon ^{3/2} N^2}. \end{aligned}$$

Error Analysis

Theorem 5

Let $y(x_i)$ be the solution of problem $(P_{\varepsilon })$ and $y_i$ the solution of $(P^N_{\varepsilon })$. Then, for N sufficiently large.

$$\begin{aligned} \max _{x_i \in \overline{\varOmega }^N_{\varepsilon }} \mid y(x_i)-y_i\mid \le C(N^{-1}\ln N)^2 \end{aligned}$$

where C is a constant independent of $\varepsilon$ and N.

Proof

Consider the discrete barrier function $\varPhi _d$ defined by

$$\begin{aligned} -\varepsilon \delta ^2\varPhi _d(x_i) + \alpha \varPhi _d(x_i) = 0 \quad \forall ~ x_i~\in ~\varOmega ^N_{\varepsilon }, \\ \varPhi _d(0)=0,~\varPhi _d(d)=1,\quad \varPhi _d(1)=0. \end{aligned}$$

From the discrete minimum principle on the separate intervals [0,d] and [d,1], one easily derives that

$$\begin{aligned} 0 \le \varPhi _d \le 1 \end{aligned}$$

and also

$$\begin{aligned} L_{\varepsilon }^N \varPhi _d (x_i) = (a(x_i)-\alpha )\varPhi _d(x_i) \ge 0, \quad \forall ~ x_i \in \varOmega ^N_{\varepsilon }. \end{aligned}$$

Define the ancillary continuous functions $u_1,u_2$ by

$$\begin{aligned} -\varepsilon u_1{^{\prime \prime }}+\alpha u_1 = 0,~u_1(0)=0,~u_1(d)=1 \\ -\varepsilon u_2{^{\prime \prime }}+\alpha u_2 = 0,~u_2(d)=1,~u_2(1)=0. \end{aligned}$$

Note that

$$\begin{aligned} u_1(x) = \dfrac{sinh(\sqrt{\alpha }x/\sqrt{\varepsilon })}{sinh(\sqrt{\alpha }d /\sqrt{\varepsilon })}, ~~ u_2(x) = \dfrac{sinh(\sqrt{\alpha }(1-x)/\sqrt{\varepsilon })}{sinh(\sqrt{\alpha }(1-d) /\sqrt{\varepsilon })} \end{aligned}$$

Define

$$\begin{aligned} \widetilde{u} = {\left\{ \begin{array}{ll} u_1(x), \quad x~\in ~(0,d) \\ u_2(x), \quad x~\in ~(d,1) \end{array}\right. } \end{aligned}$$

Hence

$$\begin{aligned} L^N_{t} \widetilde{u}&= \dfrac{sinh\left( \dfrac{\sqrt{\alpha }(d-2h^-)}{\sqrt{\varepsilon }}\right) - 4 sinh\left( \dfrac{\sqrt{\alpha }(d-h^-)}{\sqrt{\varepsilon }}\right) }{2h^- sinh\left( \dfrac{\sqrt{\alpha d}}{\sqrt{\varepsilon }}\right) } + \dfrac{3}{2h^-} \\&- \dfrac{-sinh\left( \dfrac{\sqrt{\alpha }(d-2h^+)}{\sqrt{\varepsilon }}\right) + 4 sinh\left( \dfrac{\sqrt{\alpha }(d-h^+)}{\sqrt{\varepsilon }}\right) }{2h^+ sinh\left( \dfrac{\sqrt{\alpha d}}{\sqrt{\varepsilon }}\right) } + \dfrac{3}{2h^+} \end{aligned}$$

Based on [3] and the result, $\rho =\dfrac{\sqrt{\alpha h}}{\sqrt{\varepsilon }},$ since $\dfrac{1-e^{-x}}{x}$ is a decreasing function of x and $\rho \le 16(N^{-1}ln N)$. Here, $h=h^+=h^-$.

We can obtain,

$$\begin{aligned} L^N_{t} \widetilde{u} \le -\dfrac{C}{\sqrt{\varepsilon }}. \end{aligned}$$

Note that by applying the results from [3] on the intervals [0,d] and [d,1] separately, if follows that

$$\begin{aligned} \mid \varPhi _d (x_i) - u_1(x_i) \mid&\le C(N^{-1}ln N)^2, \quad i \le N/2 \\ \mid \varPhi _d (x_i) - u_2(x_i) \mid&\le C(N^{-1}ln N)^2, \quad i \ge N/2. \end{aligned}$$

For i=N/2,

$$\begin{aligned} L^N_{t} \varPhi _d(d)&= \dfrac{-\varPhi _d(d+2h^+)+4\varPhi _d(d+h^+)-3}{2h^+} - \dfrac{\varPhi _d(d-2h^-)-4\varPhi _d(d-h^-)+3}{2h^-} \\&= L^N_t \widetilde{u} \pm \dfrac{Ch^2}{\varepsilon ^{3/2}} \\&= \dfrac{C}{\sqrt{\varepsilon }} + \dfrac{C (N^{-1}ln N)^2}{\sqrt{\varepsilon }}\\ L^N_{t} \varPhi _d(d)&\le -\dfrac{C_1}{\sqrt{\varepsilon }} \end{aligned}$$

For N sufficiently large, consider the mesh function

$$\begin{aligned} W(x_i) = C_2(N^{-1}ln N)^2 + \dfrac{C_3h^2}{\varepsilon }\varPhi _d(x_i) \pm e(x_i) \end{aligned}$$

where $C_2$ and $C_3$ are suitably large constants. Hence for $i \ne N/2$

$$\begin{aligned} L_c^N W(x_i) = C_2 a(x_i)(N^{-1}ln N)^2 + C_3 \dfrac{h^2}{\varepsilon }(a(x_i) - \alpha ) \varPhi _d(x_i) \pm L^N_c e(x_i) \ge 0 \end{aligned}$$

Hence for suitably large $C_2,C_3$, for i = N/2

$$\begin{aligned} L_{t}^N W(d) \le 0. \end{aligned}$$

Thus, for N sufficiently large,

$$\begin{aligned} \mid y(x_i) - y_i \mid \le C (N^{-1} ln N)^2 \end{aligned}$$

which complete the proof. $\square$

Numerical Experiments

In this section we experimentally verify our theoretical results proved in the previous section.

Example 1

We consider the problem (1)–(2) with

$$\begin{aligned} b(x) =1.0, f(x) = {\left\{ \begin{array}{ll} \quad 0.7, \quad x \le 0.5,\\ -0.6, \quad x > 0.5, \end{array}\right. }\text {and}~y(0)=1,~y(1)=0. \end{aligned}$$

Example 2

Consider the problem (1)–(2) with

$$\begin{aligned} b(x) = {\left\{ \begin{array}{ll} (2x+1), \quad x \le 0.5,\\ (3-2x), \quad x > 0.5, \end{array}\right. } f(x) = {\left\{ \begin{array}{ll} -0.5, \quad x \le 0.5,\\ \quad 0.5, \quad x > 0.5, \end{array}\right. }\text {and}~y(0) = y(1) = f(0) \end{aligned}$$

The nodal errors and order of convergence are estimated using the double mesh principle [17]. Define the double mesh difference to be

$$\begin{aligned} D^N_{\varepsilon } = \max _{x_i \in \overline{\varOmega }^N_{\varepsilon }} \mid y_{\varepsilon }^N (x_i) - y_{\varepsilon }^{2N} (x_i) \mid \end{aligned}$$

The rates of convergence $\rho ^N$ are computed from

$$\begin{aligned} \rho ^N = log_2 \left( \dfrac{D^N_{\varepsilon }}{D^{2N}_{\varepsilon }} \right) , \end{aligned}$$

In Tables 1 and 2, we present values of $D^N_{\varepsilon }$ and $\rho ^N$ for the Example 1 respectively (Figs. 1, 2). Similarly in Tables 3 and 4, we present values of $D^N_{\varepsilon }$ and $\rho ^N$ for the Example 2 respectively (Figs. 3, 4).

Fig. 1

Numerical Solution for $N=128 \,\text {and}\,\varepsilon \,=\,10^{-3}$ for Example 1

Fig. 2

Error graph for $N=128 \,\text {and}\,\varepsilon \,=\,10^{-3}$ for Example 1

Fig. 3

Numerical Solution for $N=128 \,\text {and}\, \varepsilon \,=\,10^{-3}$ for Example 2

Fig. 4

Error graph for $N=128 \,\text {and}\, \varepsilon \,=\,10^{-3}$for Example 2

Table 1 Maximum point-wise errors $E_\varepsilon ^N$ for various $N$ and $\varepsilon$ for the Problem 1

Table 2 Order of convergence for various $N$ and $\varepsilon$ for the problem 1

Table 3 Maximum point-wise errors $E_\varepsilon ^N$ for various $N$ and $\varepsilon$ for the Problem 2

Table 4 Order of convergence for various $N$ and $\varepsilon$ for the problem 2