Abstract
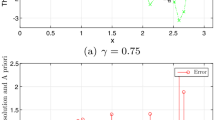
In this work, we study an inverse problem to determine an unknown source term for fractional diffusion equation with Riemann–Liouville derivative. In general, the problem is severely ill posed in the sense of Hadamard. To regularize the unstable solution of the problem, we have applied the quasi-boundary value method. In the theoretical result, we show the error estimate between the exact solution and regularized solution with a priori parameter choice rules and analyze it. Eventually, a numerical example has been carried out, the result shows that our regularization method is converged.

Similar content being viewed by others
References
Calvo MP, Cuesta E, Palencia C (2007) Runge–Kutta convolution quadrature methods for well-posed equations with memory. Numer Math 107(4):589–614
Carillo S, Valente V, Caffarelli GV (2013) A linear viscoelasticity problem with a singular memory kernel: an existence and uniqueness result. Differ Integral Equ 26(9–10):1115–1125
Carillo S, Valente V, Caffarelli GV (2014) Heat conduction with memory: a singular kernel problem. Evol Equ Control Theory 3(3):399–410
Clark GW, Oppenheimer SF (1994) Quasireversibility methods for non-well posed problems. Electron J Differ Equ 301(8):1–9
Denche M, Bessila K (2005) A modified quasi-boundary value method for ill-posed problems. J Math Anal Appl 301:419–426
Desch W, Grimmer R (1989) Smoothing properties of linear Volterra integrodifferential equations. SIAM J Math Anal 20(1):116–132
Hirata H, Miao C (2002) Space-time estimates of linear flow and application to some nonlinear integro-differential equations corresponding to fractional-order time derivative. Adv Differ Equ 2:217–236
Ismailov MI, Cicek M (2016) Inverse source problem for a time-fractional diffusion equation with nonlocal boundary conditions. Appl Math Model 40:4891–4899
Kirsch A (2011) An introduction to the mathematical theory of inverse problems, Volume 120 of applied mathematical sciences, 2nd edn. Springer, New York
Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations, Volume 204 (North-Holland Mathematics Studies). Elsevier Science Inc., New York
Kirane M, Malik AS, Al-Gwaiz MA (2013) An inverse source problem for a two dimensional time fractional diffusion equation with nonlocal boundary conditions. Math Methods Appl Sci 36(9):1056–1069
Kirane M, Malik AS (2011) Determination of an unknown source term and the temperature distribution for the linear heat equation involving fractional derivative in time. Appl Math Comput 218(1):163–170
Khorshidi MN, Yousefi SA (2017) Determination of an unknown source term for an inverse source problem of the time-fractional equation. Asian Eur J Math 10:1750031
Kochubei AN (2014) Cauchy problem for fractional diffusion-wave equations with variable coefficients. Appl Anal 93(10):2211–2242
Podlubny I (1999) Fractional differential equations. Academic Press, London
Podlubny I, Kacenak M (2006) Mittag–Leffler function. The MATLAB routine. http://www.mathworks.com/matlabcentral/fileexchange. Accessed 5 Aug 2019
Ruan Z, Wang Z (2017) Identification of a time-dependent source term for a time-fractional diffusion equation problem. Appl Anal 96:1638–1655
Ruan Z, Zhang S, Xiong S (2018) Solving an inverse source problem for a time-fractional diffusion equation by a modified quasi-boundary value method. Evol Equ Control Theory 7:669–682
Sakamoto K, Yamamoto M (2011) Initial value/boudary value problems for fractional diffusion-wave equations and applications to some inverse problems. J Math Anal Appl 382:426–447
Schneider WR, Wyss W (1989) Fractional diffusion and wave equations. J Math Phys 30(1):134–144
Tuan NH, Long LD, Thinh NV (2016) Regularized solution of an inverse source problem for a time fractional diffusion equation. Appl Math Model 40(19–20):8244–8264
Wang JG, Zhou YB, Wei T (2013) Two regularization methods to identify a space-dependent source for the time-fractional diffusion equation. Appl Numer Math 68:39–57
Wei T, Wang J (2014) A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation. Appl Numer Math 78:95–111
Wei T, Li XL, Li YS (2016) An inverse time-dependent source problem for a time-fractional diffusion equation. Inverse Probl 32:085003
Wei T, Zhang ZQ (2013) Reconstruction of a time-dependent source term in a time-fractional diffusion equation. Eng Anal Bound Elem 37:23–31
Zhang ZQ, Wei T (2013) Identifying an unknown source in time-fractional diffusion equation by a truncation method. Appl Math Comput 219(11):5972–5983
Zhou Y (2014) Basic theory fractional differential equations. World Scientific, Singapore
Acknowledgements
This research was supported by the Macau Science and Technology Development Fund (Grant no. 0074/2019/A2) from the Macau Special Administrative Region of the P.R. China.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by José Tenreiro Machado.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Tuan, N.H., Zhou, Y., Long, L.D. et al. Identifying inverse source for fractional diffusion equation with Riemann–Liouville derivative. Comp. Appl. Math. 39, 75 (2020). https://doi.org/10.1007/s40314-020-1103-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-020-1103-2