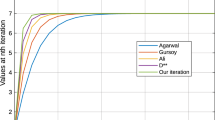
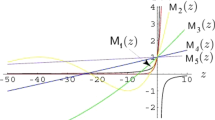
Abstract
In this study, we introduce the concept of admissible \(\alpha\)-\(\eta\)-\(\mathcal {F}\)-simulation fuzzy contraction mappings as an innovative extension within the realm of fuzzy contraction notions. The investigation systematically establishes the existence and uniqueness of fixed points pertaining to this category of mappings. To validate the precision of our findings, we apply the proposed concept to fractional integro-differential equations. The outcomes of our research serve to fortify, extend, and consolidate various antecedent studies within the academic literature.
Similar content being viewed by others
Data availability
Not applicable.
References
Abdo MS, Panchal SK (2018) Weighted fractional neutral functional differential equations. J Sib Fed Univ Math Phys 11(5):535–549
Boulares H, Benchaabane A, Pakkaranang N, Shafqat R, Panyanak B (2022) Qualitative Properties of Positive Solutions of a Kind for Fractional Pantograph Problems using Technique Fixed Point Theory. Fractal Fract 6:593
Boulares H, Meftah B, Moumen A, Shafqat R, Saber H, Alraqad T, Ali EE (2023) Fractional multiplicative bullen-type inequalities for multiplicative differentiable functions. Symmetry 15:451
Dosenovic T, Rakic D, Radenovic S, Caric B (2023) \(\acute{C}\)iri\(\acute{c}\) type nonunique fixed point theorems in the frame of fuzzy metric spaces. AIMS Math 8(1):2154–2167
George A, Veeramani P (1994) On some results in fuzzy metric spaces. Fuzzy Sets Syst 64(3):395–399
Grabiec M (1988) Fixed points in fuzzy metric spaces. Fuzzy Sets Syst 27(3):385–389
Gregori V, Sapena A (2002) On fixed-point theorems in fuzzy metric spaces. Fuzzy Sets Syst 125:245–252
Hayel NS, Khan IA, Imdad M, Alfaqih WM (2019) New fuzzy \(\varphi\)-fixed point results employing a new class of fuzzy contractive mappings. J Intell Fuzzy Syst 37(4):5391–5402
Huang H, Carić B, Dosenovic T, Rakić D, Brdar M (2021) Fixed-point theorems in fuzzy metric spaces via fuzzy F-contraction. Mathematics 9(6):641
Jleli M, Samet B (2014) A new generalization of the Banach contraction principle. J Inequal Appl 2014(1):38
Khojasteh F, Shukla S, Radenović S (2015) A new approach to the study of fixed point theory for simulation functions. Filomat 29(6):1189–1194
Kramosil I, Michalek J (1975) Fuzzy metrics and statistical metric spaces. Kybernetika 11(5):336–344
Melliani S, Moussaoui A (2018) Fixed point theorem using a new class of fuzzy contractive mappings. J Univ Math 1(2):148–154
Melliani S, Moussaoui A, Chadli LS (2020) Admissible almost type \(Z\)-contractions and fixed point results. Int J Math Math Sci 2020:1–7
Mihet D (2008) Fuzzy \(\psi\)-contractive mappings in non-Archimedean fuzzy metric spaces. Fuzzy Sets Syst 159(6):739–744
Moumen A, Boulares H, Meftah B, Shafqat R, Alraqad T, Ali EE, Khaled Z (2023) Multiplicatively simpson type inequalities via fractional integral. Symmetry 15:460
Moussaoui A, Hussain N, Melliani S (2021) Global optimal solutions for proximal fuzzy contractions involving control functions. J Math 2021:6269304
Moussaoui A, Hussain N, Melliani S, Hayel N, Imdad M (2022) Fixed point results via extended \(\cal{FZ}\)-simulation functions in fuzzy metric spaces. J Inequal Appl 2022:69
Moussaoui A, Saleem N, Melliani S, Zhou M (2022) Fixed point results for new types of fuzzy contractions via admissible functions and \(FZ\)-simulation functions. Axioms 11:87
Moussaoui A, Todorcevic V, Pantović M, Radenović S, Melliani S (2023) Fixed point results via \(\cal{G}\)-transitive binary relation and fuzzy \(\cal{L}\)-\(\cal{R}\)-contraction. Mathematics 11:1768
Naimi A, Brahim T, Zennir K (2022) Existence and stability results for the solution of neutral fractional integro-differential equation with nonlocal conditions. Tamkang J Math 53:239–257
Patel UD, Radenović S (2022) An application to nonlinear fractional differential equation via \(\alpha\)-\(\Gamma F\)-fuzzy contractive mappings in a fuzzy metric space. Mathematics 10:2831
Salem S, Ahmed B, Alsaedi A, Ntouyas SK (2019) Fractional differential equation involving mixed nonlinearities with nonlocal multi-point and Reimann-Steiljes integral-multi-stripconditions. Fractal Fract J 34(3):1–16
Salimi P, Latif A, Hussain N (2013) Modified \(\alpha\)-\(\psi\)-contractive mappings with applications. Fixed Point Theory Appl 2013:151
Samet B, Vetro C, Vetro P (2012) Fixed point theorems for \(\alpha\)-\(\psi\)-contractive mappings. Nonlinear Anal 75:2154–2165
Schweizer B, Sklar A (1960) Statistical metric spaces. Pac J Math 10(1):313–334
Wardowki D (2013) Fuzzy contractive mappings and fixed points in fuzzy metric spaces. Fuzzy Sets Syst 222:108–114
Wardowski D (2012) Fixed points of a new type of contractive mappings in complete spaces. Fixed Point Theory Appl 2012:94
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Funding
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Moussaoui, A., Melliani, S. Fixed point results under admissible \(\alpha\)-\(\eta\)-\(\mathcal {F}\)-simulation fuzzy contraction with application. Int J Syst Assur Eng Manag 15, 3807–3816 (2024). https://doi.org/10.1007/s13198-024-02378-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-024-02378-9