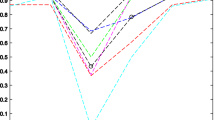
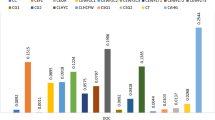
Abstract
Yager (2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), 10.1109/ifsa-nafips.2013.6608375, 2013) first proposed the notion of Pythagorean fuzzy sets (PFS), which provides a unique procedure to characterize vagueness and uncertainty with greater accuracy and precision than intuitionistic fuzzy sets (IFS). The notion was established mathematically to explain vagueness and ambiguity and to deliver a structured instrument for dealing with vagueness in real-world situations. In this paper, performance of similarity measures of PFS based on the secant function, considering participation grade, non- participation grade, and hesitancy have been established. Axioms related to similarity measures have also been proved for the proposed measures. These similarity measurements, as well as weighted similarity measures between PFS have then been used for the performance of recognition of patterns and medical analysis. Two case studies have been provided to highlight the utility of similarity measures. Finally, to determine the efficacy of the recommended measures, a comparative study is also conducted.


Similar content being viewed by others
References
Arora HD, Kumar V (2021) Study of fuzzy distance measure and its application to medical diagnosis. Informatica. https://doi.org/10.31449/inf.v45i1.3199
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96. https://doi.org/10.1016/s0165-0114(86)80034-3
Atanassov KT (1989) More on intuitionistic fuzzy sets. Fuzzy Sets Syst 33(1):37–45. https://doi.org/10.1016/0165-0114(89)90215-7
Bustince H, Barrenechea E, Pagola M (2006) Restricted equivalence functions. Fuzzy Sets Syst 157(17):2333–2346. https://doi.org/10.1016/j.fss.2006.03.018
Bustince H, Barrenechea E, Pagola M (2007) Image thresholding using restricted equivalence functions and maximizing the measures of similarity. Fuzzy Sets Syst 158(5):496–516. https://doi.org/10.1016/j.fss.2006.09.012
Chen S-M, Cheng S-H, Lan T-C (2016) Multicriteria decision making based on the TOPSIS method and similarity measures between intuitionistic fuzzy values. Inf Sci 367–368:279–295. https://doi.org/10.1016/j.ins.2016.05.044
Dengfeng L, Chuntian C (2002) New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recogn Lett 23(1–3):221–225. https://doi.org/10.1016/s0167-8655(01)00110-6
Ejegwa PA (2018) Distance and similarity measures for Pythagorean fuzzy sets. Granular Comput 5(2):225–238. https://doi.org/10.1007/s41066-018-00149-z
Ejegwa PA (2020) New similarity measures for Pythagorean fuzzy sets with applications. Int J Fuzzy Comput Modell 3(1):75–94. https://doi.org/10.1504/ijfcm.2020.106105
Gong YB (2011) A new similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Adv Mater Res 219–220:160–164. https://doi.org/10.4028/www.scientific.net/amr.219-220.160
Hung K-C, Wang P-K (2013) An integrated intuitionistic fuzzy similarity measures for medical problems. Int J Comput Intell Syst 7(2):327–343. https://doi.org/10.1080/18756891.2013.856259
Hung W-L, Yang M-S (2004) Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance. Pattern Recogn Lett 25(14):1603–1611. https://doi.org/10.1016/j.patrec.2004.06.006
Hwang C-M, Yang M-S, Hung W-L, Lee M-G (2012) A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition. Inf Sci 189:93–109. https://doi.org/10.1016/j.ins.2011.11.029
Immaculate H, Ebenanjar E, Terence S (2018) A new similarity measure based on cotangent function for multi period medical diagnosis. Int J Mech Eng Technol (IJMET) 9(10):1285–1293
Li D, Zeng W (2017) Distance measure of pythagorean fuzzy sets. Int J Intell Syst 33(2):348–361. https://doi.org/10.1002/int.21934
Li Y, Olson DL, Qin Z (2007) Similarity measures between intuitionistic fuzzy (vague) sets: a comparative analysis. Pattern Recogn Lett 28(2):278–285. https://doi.org/10.1016/j.patrec.2006.07.009
Liang D, Xu Z (2017) The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl Soft Comput 60:167–179. https://doi.org/10.1016/j.asoc.2017.06.034
Maoying T (2013) A new fuzzy similarity based on cotangent function for medical diagnosis. Adv Model Optim. 15(2):151–156
Mohd WRW, Abdullah L (2018) Similarity measures of Pythagorean fuzzy sets based on combination of cosine similarity measure and Euclidean distance measure. In: AIP conference proceedings. https://doi.org/10.1063/1.5041661
Muthukumar P, Krishnan GSS (2016) A similarity measure of intuitionistic fuzzy soft sets and its application in medical diagnosis. Appl Soft Comput 41:148–156. https://doi.org/10.1016/j.asoc.2015.12.002
Nguyen XT, Nguyen VD, Nguyen VH, Garg H (2019) Exponential similarity measures for Pythagorean fuzzy sets and their applications to pattern recognition and decision-making process. Complex Intell Syst 5(2):217–228. https://doi.org/10.1007/s40747-019-0105-4
Peng X (2019) New similarity measure and distance measure for Pythagorean fuzzy set. Complex Intell Syst 5(2):101–111. https://doi.org/10.1007/s40747-018-0084-x
Peng X, Garg H (2019) Multiparametric similarity measures on Pythagorean fuzzy sets with applications to pattern recognition. Appl Intell 49(12):4058–4096. https://doi.org/10.1007/s10489-019-01445-0
Peng X, Yang Y (2015) Some results for pythagorean fuzzy sets. Int J Intell Syst 30(11):1133–1160. https://doi.org/10.1002/int.21738
Peng X, Yuan H, Yang Y (2017) Pythagorean fuzzy information measures and their applications. Int J Intell Syst 32(10):991–1029. https://doi.org/10.1002/int.21880
Rajarajeswari P, Uma N (2013) Intuitionistic fuzzy multi-similarity measure based on cotangent function. Int J Eng Res Technol. 2(11):1323–1329
Shi LL, Ye J (2013) Study on fault diagnosis of turbine using an improved cosine similarity measure for vague sets. J Appl Sci 13(10):1781–1786. https://doi.org/10.3923/jas.2013.1781.1786
Son LH, Phong PH (2016) On the performance evaluation of intuitionistic vector similarity measures for medical diagnosis 1. J Intell Fuzzy Syst 31(3):1597–1608. https://doi.org/10.3233/JIFS-151654
Song Y, Wang X, Lei L, Xue A (2014) A novel similarity measure on intuitionistic fuzzy sets with its applications. Appl Intell 42(2):252–261. https://doi.org/10.1007/s10489-014-0596-z
Szmidt E, Kacprzyk J (2005) A new concept of a similarity measure for intuitionistic fuzzy sets and its use in group decision making. In: Modeling decisions for artificial intelligence, pp 272–282. https://doi.org/10.1007/11526018_27
Szmidt E, Kacprzyk J (2000) Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst 114(3):505–518. https://doi.org/10.1016/s0165-0114(98)00244-9
Wei G, Wei Y (2018) Similarity measures of Pythagorean fuzzy sets based on the cosine function and their applications. Int J Intell Syst 33(3):634–652. https://doi.org/10.1002/int.21965
Wei C-P, Wang P, Zhang Y-Z (2011) Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications. Inf Sci 181(19):4273–4286. https://doi.org/10.1016/j.ins.2011.06.001
Yager RR (2013) Pythagorean fuzzy subsets. In: 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS). https://doi.org/10.1109/ifsa-nafips.2013.6608375
Yager RR (2014) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965. https://doi.org/10.1109/tfuzz.2013.2278989
Yager RR (2015) Properties and applications of pythagorean fuzzy sets. In: Imprecision and uncertainty in information representation and processing, pp 119–136. https://doi.org/10.1007/978-3-319-26302-1_9
Ye J (2010) Multicriteria group decision-making method using vector similarity measures for trapezoidal intuitionistic fuzzy numbers. Group Decis Negot 21(4):519–530. https://doi.org/10.1007/s10726-010-9224-4
Ye J (2011) Cosine similarity measures for intuitionistic fuzzy sets and their applications. Math Comput Model 53(1–2):91–97. https://doi.org/10.1016/j.mcm.2010.07.022
Ye J (2012) Multicriteria decision-making method using the Dice similarity measure between expected intervals of trapezoidal fuzzy numbers. J Decis Syst 21(4):307–317. https://doi.org/10.1080/12460125.2012.734265
Ye J (2015) Similarity measures of intuitionistic fuzzy sets based on cosine function for the decision-making of mechanical design schemes. J Intell Fuzzy Syst 30(1):151–158. https://doi.org/10.3233/ifs-151741
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353. https://doi.org/10.1016/s0019-9958(65)90241-x
Zeng S, Chen J, Li X (2016) A hybrid method for pythagorean fuzzy multiple-criteria decision making. Int J Inf Technol Decis Mak 15(02):403–422. https://doi.org/10.1142/s0219622016500012
Zeng W, Li D, Yin Q (2018) Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int J Intell Syst 33(11):2236–2254. https://doi.org/10.1002/int.22027
Zhang X (2015) A Novel approach based on similarity measure for pythagorean fuzzy multiple criteria group decision making. Int J Intell Syst 31(6):593–611. https://doi.org/10.1002/int.21796
Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with pythagorean fuzzy sets. Int J Intell Syst 29(12):1061–1078. https://doi.org/10.1002/int.21676
Zhang QS, Yao HX, Zhang ZH (2010) Some similarity measures of interval-valued intuitionistic fuzzy sets and application to pattern recognition. Appl Mech Mater 44–47:3888–3892. https://doi.org/10.4028/www.scientific.net/amm.44-47.3888
Zhang Q, Hu J, Feng J, Liu A, Li Y (2019) New similarity measures of pythagorean fuzzy sets and their applications. IEEE Access 7:138192–138202. https://doi.org/10.1109/access.2019.2942766
Zulqarnain M, Dayan F (2017) Selection Of best alternative for an automotive company by intuitionistic fuzzy TOPSIS method. Int J Sci Technol Res 6(10):126–132
Zulqarnain RM, Abdai S, Ali B, Ali L, Dayan F, Ahamad MI, Zafar Z (2020a) Slection of medical clinic diagnosis by using TOPSIS method. Int J Pharm Sci Rev Res 61(1):22–27
Zulqarnain RM, Abdal S, Maalik A, Ali B, Zafar Z, Ahamad MI, Younas S, Mariam A, Dayan F (2020b) Application of TOPSIS method in decision making via soft set. Biomed J Sci Tech Res 24(3):18208–18215
Zulqarnain RM, Siddique I, Ahmad S, Iampan A, Jovanov G, Vranješ Đ, Vasiljević J (2021) Pythagorean fuzzy soft Einstein ordered weighted average operator in sustainable supplier selection problem. Math Probl Eng 2021:e2559979. https://doi.org/10.1155/2021/2559979
Zulqarnain RM et al (2022a) Einstein-ordered weighted geometric operator for pythagorean fuzzy soft set with its application to solve MAGDM problem. Math Probl Eng 2022:1–14. https://doi.org/10.1155/2022/5199427
Zulqarnain RM, Siddique I, Jarad F, Hamed YS, Abualnaja KM, Iampan A (2022b) Einstein aggregation operators for pythagorean fuzzy soft sets with their application in multiattribute group decision-making. J Funct Spaces 2022:1–21. https://doi.org/10.1155/2022/1358675
Funding
The authors did not receive support from any organization for the submitted work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose. The authors have no conflicts of interest to declare that are relevant to the content of this article. All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript. The authors have no financial or proprietary interests in any material discussed in this article.
Ethical approval
For this type of study, informed consent is not required.
Informed consent
No Informed consent was required in the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Arora, H.D., Naithani, A. Evaluating performance of novel similarity measures of Pythagorean fuzzy sets and their applications in pattern recognition and medical diagnosis. Int J Syst Assur Eng Manag 15, 3485–3494 (2024). https://doi.org/10.1007/s13198-024-02355-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-024-02355-2
Keywords
- Intuitionistic fuzzy set
- Pythagorean fuzzy sets
- Similarity measure
- Medical diagnosis and pattern recognition