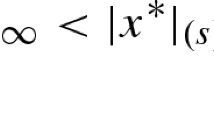iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s11590-019-01506-w
A concave optimization-based approach for sparse multiobjective programming | Optimization Letters Skip to main content
Springer Nature Link
Log in

A concave optimization-based approach for sparse multiobjective programming

  • Original Paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

Abstract

The paper is concerned with multiobjective sparse optimization problems, i.e. the problem of simultaneously optimizing several objective functions and where one of these functions is the number of the non-zero components (or the \(\ell _0\)-norm) of the solution. We propose to deal with the \(\ell _0\)-norm by means of concave approximations depending on a smoothing parameter. We state some equivalence results between the original nonsmooth problem and the smooth approximated problem. We are thus able to define an algorithm aimed to find sparse solutions and based on the steepest descent framework for smooth multiobjective optimization. The numerical results obtained on a classical application in portfolio selection and comparison with existing codes show the effectiveness of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. A computation of the vector F(x) counts as a single function evaluation. A computation of the gradient vector \(\nabla F(x)\) counts as n function evaluations.

  2. The other algorithms do not provide this functionality.

  3. For the DTS1, DTS2 and DTS3, n is equal to 12, 24, 48, respectively. For the FF datasets, n is equal to 10, 17 and 48, respectively.

  4. The functions are made continuously differentiable by removing the 1/4 roots.

  5. The NOMAD algorithm is not reported since the available implementation does not support problems with more than 2 objectives.

References

  1. Abramson, M.A., Audet, C., Couture, G., Dennis, Jr., J.E., Le Digabel, S., Tribes, C.: The NOMAD project. Software available at https://www.gerad.ca/nomad/

  2. Amaldi, E., Kann, V.: On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems. Theor. Comput. Sci. 209(1–2), 237–260 (1998)

    Article  MathSciNet  Google Scholar 

  3. Ansary, M.A.T., Panda, G.: A sequential quadratically constrained quadratic programming technique for a multi-objective optimization problem. Eng. Optim. 51(1), 22–41 (2019)

    Article  MathSciNet  Google Scholar 

  4. Beume, N., Naujoks, B., Emmerich, M.: SMS-EMOA: multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 181(3), 1653–1669 (2007)

    Article  Google Scholar 

  5. Brito, R.P., Vicente, L.N.: Efficient cardinality/mean-variance portfolios. In: System Modeling and Optimization. Springer Series IFIP Advances in Information and Communication Technology, pp. 52–73. Springer, Berlin (2014)

  6. Cocchi, G., Liuzzi, G., Papini, A., Sciandrone, M.: An implicit filtering algorithm for derivative-free multiobjective optimization with box constraints. Comput. Optim. Appl. 69(2), 267–296 (2018)

    Article  MathSciNet  Google Scholar 

  7. Custódio, A.L., Madeira, J.F.A., Vaz, A.I.F., Vicente, L.N.: Direct multisearch for multiobjective optimization. SIAM J. Optim. 21(3), 1109–1140 (2011)

    Article  MathSciNet  Google Scholar 

  8. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T.: A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6(2), 182–197 (2002)

    Article  Google Scholar 

  9. Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91(2), 201–213 (2002)

    Article  MathSciNet  Google Scholar 

  10. Ehrgott, M.: Multicriteria Optimization. Springer, Berlin (2005)

    MATH  Google Scholar 

  11. El Moudden, M., El Ghali, A.: Multiple reduced gradient method for multiobjective optimization problems. Numer. Algorithms 79(4), 1257–1282 (2018)

    Article  MathSciNet  Google Scholar 

  12. El Moudden, M., El Ghali, A.: A new reduced gradient method for solving linearly constrained multiobjective optimization problems. Comput. Optim. Appl. 71(3), 719–741 (2018)

    Article  MathSciNet  Google Scholar 

  13. Fan, L., Yoshino, T., Xu, T., Lin, Y., Liu, H.: A novel hybrid algorithm for solving multiobjective optimization problems with engineering applications. Math. Probl. Eng. 2018, 1–15 (2018)

    MathSciNet  MATH  Google Scholar 

  14. Fazzio, N.S., Schuverdt, M.L.: Convergence analysis of a nonmonotone projected gradient method for multiobjective optimization problems. Optim. Lett. 13, 1365–1379 (2018)

    Article  MathSciNet  Google Scholar 

  15. Fliege, J., Svaiter, B.: Steepest descent methods for multicriteria optimization. Math. Methods Oper. Res. 51(3), 479–494 (2000)

    Article  MathSciNet  Google Scholar 

  16. Fliege, J., Vaz, A.: A method for constrained multiobjective optimization based on SQP techniques. SIAM J. Optim. 26(4), 2091–2119 (2016)

    Article  MathSciNet  Google Scholar 

  17. Fukuda, E.H., Drummond, L.M.G.: A survey on multiobjective descent methods. Pesqui. Oper. 34(3), 585–620 (2014)

    Article  Google Scholar 

  18. Gebken, B., Peitz, S., Dellnitz, M.: A descent method for equality and inequality constrained multiobjective optimization problems. In: Trujillo, L., Schütze, O., Maldonado, Y., Valle, P. (eds.) Numerical and Evolutionary Optimization—NEO 2017, pp. 29–61. Springer, Cham (2019)

    Chapter  Google Scholar 

  19. Gong, M., Liu, J., Li, H., Cai, Q., Su, L.: A multiobjective sparse feature learning model for deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 26(12), 3263–3277 (2015)

    Article  MathSciNet  Google Scholar 

  20. Li, L., Yao, X., Stolkin, R., Gong, M., He, S.: An evolutionary multiobjective approach to sparse reconstruction. IEEE Trans. Evol. Comput. 18(6), 827–845 (2014)

    Article  Google Scholar 

  21. Liuzzi, G., Lucidi, S., Rinaldi, F.: A derivative-free approach to constrained multiobjective nonsmooth optimization. SIAM J. Optim. 26(4), 2744–2774 (2016)

    Article  MathSciNet  Google Scholar 

  22. Lorenzo, D.D., Liuzzi, G., Rinaldi, F., Schoen, F., Sciandrone, M.: A concave optimization-based approach for sparse portfolio selection. Optim. Methods Softw. 27(6), 983–1000 (2012)

    Article  MathSciNet  Google Scholar 

  23. Lucambio Pérez, L., Prudente, L.: Nonlinear conjugate gradient methods for vector optimization. SIAM J. Optim. 28(3), 2690–2720 (2018)

    Article  MathSciNet  Google Scholar 

  24. MathWorks: MATLAB R2018b Global Optimization Toolbox v4.0. The MathWorks, Natick, MA (2018)

    Google Scholar 

  25. Miettinen, K.: Nonlinear Multiobjective Optimization. International Series in Operations Research & Management Science. Springer, Berlin (1998)

    Book  Google Scholar 

  26. Rinaldi, F., Schoen, F., Sciandrone, M.: Concave programming for minimizing the zero-norm over polyhedral sets. Comput. Optim. Appl. 46(3), 467–486 (2010)

    Article  MathSciNet  Google Scholar 

  27. Sinan Hasanoglu, M., Dolen, M.: Multi-objective feasibility enhanced particle swarm optimization. Eng. Optim. 50(12), 2013–2037 (2018)

    Article  MathSciNet  Google Scholar 

  28. Wagner, M., Bringmann, K., Friedrich, T., Neumann, F.: Efficient optimization of many objectives by approximation-guided evolution. Eur. J. Oper. Res. 243(2), 465–479 (2015)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Ingegneria dell’Informazione, Università di Firenze, Via di Santa Marta 3, 50139, Florence, Italy

    Guido Cocchi, Tommaso Levato & Marco Sciandrone

  2. Istituto di Analisi dei Sistemi ed Informatica, Consiglio Nazionale delle Ricerche, Via dei Taurini 19, 00185, Rome, Italy

    Giampaolo Liuzzi

Authors
  1. Guido Cocchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tommaso Levato
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Giampaolo Liuzzi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Marco Sciandrone
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Giampaolo Liuzzi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cocchi, G., Levato, T., Liuzzi, G. et al. A concave optimization-based approach for sparse multiobjective programming. Optim Lett 14, 535–556 (2020). https://doi.org/10.1007/s11590-019-01506-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-019-01506-w

Keywords

Search

Navigation