Phase Noise Suppression in MIMO LoS Systems for High Capacity Backhauling

Abstract

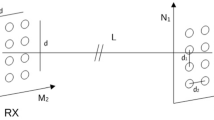
The ambitious capacity and pervasiveness requirements for future broadband wireless networks pose new challenges in the design of high capacity point-to-point (PtP) wireless microwave backhaul links. Multiple input multiple output (MIMO) architectures are the main solution for multiplying the wireless links capacity and their effectiveness has been already demonstrated in the PtP case, where channel propagation is dominated by the line-of-sight (LoS) component. In this paper we investigate the impact and performance of suppression methods for one of the main impairments in these systems, i.e. phase noise. In LoS-MIMO systems, the phase noise impact increases as the channel matrix leaves the orthogonality condition, in order to achieve practical antenna spacings and link distances. Here architectures for phase noise suppression based on pilots patterns are compared and discussed for the LoS-MIMO $(2 \times 2)$ system, revealing the advantages and numerical performance of the design options.

Appendix: A Wiener filter for the \(2 \times 2\) LoS-MIMO

The variables (12) are observed during $F$ pilot periods, each one of length $P$ symbols, generating $(F+1)$ observables. These variables are collected in the column vector $\varvec{\eta }_{lP}$, where $lP$ is the current pilot time instant. Observations span from $(lP-L)$ to $(lP-L+{FP})$ with $L=\lfloor {F/2}\rfloor {P}$. From vector $\varvec{\eta }_{lP}$, of length $4(F+1)$,

(33)

the cross covariance matrix ${\varvec{C}}_{\eta \eta }$ with dimension $4(F+1)\times 4(F+1)$ is computed as

$$\begin{aligned} {\varvec{C}}_{\eta \eta }=E_l\left[ \varvec{\eta }_{lP}\varvec{\eta }^{T}_{lP}\right] . \end{aligned}$$

(34)

Its generic element in position $(i,j)$ can be expressed as

$$\begin{aligned} {\varvec{C}}_{\eta \eta }(i,j)=E_l\left[ \eta _{m_{1}n_{1};lP} \cdot \eta _{m_{2}n_{2};lP+\varDelta }\right] =r_{m_{1}n_{1};m_{2}n_{2}}(\varDelta ), \end{aligned}$$

(35)

with $m_{1},n_{1},m_{2},n_{2}=1,2$, $\varDelta \in [-FP:P:FP]$, $i=[(F+1)(m_1-1+(n_1-1)2(F+1))+|\varDelta /P|+1]$ and $j=[(F+1)(m_2-1+(n_2-1)2(F+1))+|\varDelta /P|+1]$, and where the cross correlation $r_{m_{1}n_{1};m_{2}n_{2}}(\varDelta )$, assuming uncorrelated phase noise processes between transmitter and receiver, can be expressed as

$$\begin{aligned} r_{m_{1}n_{1};m_{2}n_{2}}(\varDelta )=r^{(R)}_{m_{1}m_{2}}(\varDelta )+r^{(T)}_{n_{1}n_{2}}(\varDelta )+\frac{\sigma ^{2}_{\scriptscriptstyle {n}}}{2}\delta (m_1-m_2)\delta (n_1-n_2)\delta (\varDelta ), \end{aligned}$$

(36)

with $r^{(R)}_{m_{1}m_{2}}$ and $r^{(T)}_{n_{1}n_{2}}$ the correlations between phase noise processes respectively at the two receivers and at the two transmitters. Only for $m_{1}=m_{2}$, $n_{1}=n_{2}$ and $\varDelta =0$ the noise term is present (additive noise contributions are assumed uncorrelated).

To estimate the phase noise processes $\widehat{\varphi }_{mn;lP+i}$, where $i=2,3, \cdots ,(P-1)$ is the interpolating symbol instant, four filter coefficients vectors of length $(F+1)$, i.e. a total of $4(F+1)$ coefficients, are computed according to

$$\begin{aligned} \mathbf w _{mn;i}={\varvec{C}}^{-1}_{\eta \eta }\mathbf c _{\eta \varphi _{mn;i}}, \end{aligned}$$

(37)

where the vector $\mathbf c _{\eta \varphi _{mn;lP+i}}$ contains the correlations $E[\varvec{\eta }_{lP}\cdot \varphi _{mn;lP+i}]$, i.e.

(38)

The four-dimensional Wiener coefficients vectors $\mathbf w _{mn;i}$, i.e.

(39)

are then used to estimate the phase noise process as sketched in Fig. 13:

$$\begin{aligned} \widehat{\varphi }_{mn;lP+i}=\mathbf w _{mn;i}^{T}\varvec{\eta }_{lP}. \end{aligned}$$

(40)

Finally, assuming i.i.d. estimation error processes w.r.t. the period $l$ and the indexes $(m,n)$, the mean squared estimation error $E[(\varphi ^e)^2]$ is defined as

$$\begin{aligned} E\left[ \left( \varphi ^e\right) ^2\right] =\frac{1}{4(P-2)}trace\left( E_l\left[ \left( \widehat{\varvec{\varphi }}_{lP}-\varvec{\varphi }_{lP}\right) \left( \widehat{\varvec{\varphi }}_{lP}-\varvec{\varphi }_{lP}\right) ^T\right] \right) , \end{aligned}$$

(41)

where the sum-processes vectors $\varvec{\varphi }_{lP}$ and $\widehat{\varvec{\varphi }}_{lP}$ have length $4(P-2)$.

Fig. 13

The four-dimensional Wiener filter block diagram