iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s11242-011-9809-7
Mixed Convection Stagnation-Point Flow Over a Vertical Plate with Prescribed Heat Flux Embedded in a Porous Medium: Brinkman-Extended Darcy Formulation | Transport in Porous Media Skip to main content
Springer Nature Link
Log in

Mixed Convection Stagnation-Point Flow Over a Vertical Plate with Prescribed Heat Flux Embedded in a Porous Medium: Brinkman-Extended Darcy Formulation

  • Published:
Transport in Porous Media Aims and scope Submit manuscript

Abstract

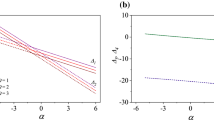
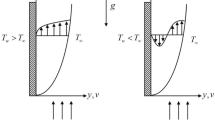
This article considers the problem of mixed convection stagnation-point flow towards a vertical plate embedded in a porous medium with prescribed surface heat flux. It is assumed that the free stream velocity and the surface heat flux vary linearly from the stagnation point. Using a similarity transformation, the governing system of partial differential equations is transformed into a system of ordinary differential equations, before being solved numerically by a finite-difference method. The features of the flow and the heat transfer characteristics are analyzed and discussed. It is found that dual solutions exist for both buoyancy assisting and opposing flows.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Bejan A., Kraus A.D.: Heat Transfer Handbook. Wiley, New York (2003)

    Google Scholar 

  • Bejan A., Dincer I., Lorente S., Miguel A.F., Reis A.H.: Porous and Complex Flow Structures in Modern Technologies. Springer, New York (2004)

    Google Scholar 

  • Brinkmann H.C.: On the permeability of media consisting of closely packed porous particles. Appl. Sci. Res. 1, 81–86 (1947)

    Article  Google Scholar 

  • Brouwers H.J.H.: Heat transfer between fluid-saturated porous medium and a permeable wall with fluid injection or withdrawal. Int. J. Heat Mass Transf. 37, 989–996 (1994)

    Article  Google Scholar 

  • Cebeci T., Bradshaw P.: Physical and Computational Aspects of Convective Heat Transfer. Springer, New York (1988)

    Book  Google Scholar 

  • Du Z.-G., Bilgen E.: Natural convection in vertical cavities with internal heat generating porous medium. Wärme- und Stoffübertr. 27, 149–155 (1992)

    Article  Google Scholar 

  • Gebhart B., Jaluria Y., Mahajan R.L., Sammakia B.: Buoyancy-Induced Flows and Transport. Hemisphere, New York (1988)

    Google Scholar 

  • Harris S.D., Ingham D.B., Pop I.: Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 77, 267–285 (2009)

    Article  Google Scholar 

  • Hong J.T., Tien C.L., Kaviany M.: Non-Darcy effects on vertical-plate natural convection in porous media with high porosities. Int. J. Heat Mass Transf. 28, 2149–2157 (1985)

    Article  Google Scholar 

  • Hong J.T., Yamada Y., Tien C.L.: Effects of non-Darcian and nonuniform porosity on vertical-plate natural convection in porous media. ASME J. Heat Transf. 109, 356–362 (1987)

    Article  Google Scholar 

  • Ingham, D.B., Pop, I. (eds): Transport Phenomenon in Porous Media III. Pergamon, Oxford (2005)

    Google Scholar 

  • Ishak A., Nazar R., Pop I.: Dual solutions in mixed convection flow near a stagnation point on a vertical surface in a porous medium. Int. J. Heat Mass Transf. 51, 1150–1155 (2008a)

    Article  Google Scholar 

  • Ishak A., Nazar R., Pop I.: Post-stagnation-point boundary layer flow and mixed convection heat transfer over a vertical, linearly stretching sheet. Arch. Mech. 60, 303–322 (2008b)

    Google Scholar 

  • Kaviany M.: Boundary-layer treatment of forced convection heat transfer from a semi-infinite flat plate embedded in porous media. ASME J. Heat Transf 109, 345–349 (1987)

    Article  Google Scholar 

  • Lauriat G., Prasad V.: Natural convection in a vertical porous cavity: a numerical study for Brinkman-extended Darcy formulation. ASME J. Heat Transf. 109, 688–696 (1987)

    Article  Google Scholar 

  • Magyari E., Pop I., Keller B.: Exact dual solutions occurring in the Darcy mixed convection flow. Int. J. Heat Mass Transf. 44, 4563–4566 (2001)

    Article  Google Scholar 

  • Merkin J.H.: On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 20, 171–179 (1985)

    Article  Google Scholar 

  • Merkin J.H., Mahmood T.: Mixed convection boundary layer similarity solutions: prescribed wall heat flux. J. Appl. Math. Phys. (ZAMP) 40, 51–68 (1989)

    Article  Google Scholar 

  • Merrill K., Beauchesne M., Previte J., Paullet J., Weidman P.: Final steady flow near a stagnation point on a vertical surface in a porous medium. Int. J. Heat Mass Transf. 49, 4681–4686 (2006)

    Article  Google Scholar 

  • Nakayama A.: PC-Aided Numerical Heat Transfer and Convective Flow. CRC Press, Tokyo (1995)

    Google Scholar 

  • Nield D.A.: ASME J. Heat Transf. 129, 1459–1963 (2007)

    Article  Google Scholar 

  • Nield D.A., Bejan A.: Convection in Porous Media (3rd edition). Springer, New York (2006)

    Google Scholar 

  • Paullet J., Weidman P.: Analysis of stagnation point flow towards a stretching sheet. Int. J. Non-Linear Mech. 42, 1084–1091 (2007)

    Article  Google Scholar 

  • Pop I., Ingham D.B.: Convective Heat Transfer: Mathematical and Computational Modelling of Viscous Fluids and Porous Media. Pergamon, Oxford (2001)

    Google Scholar 

  • Postelnicu A., Pop I.: Falkner-Skan boundary layer flow of a power-law fluid past a stretching wedge. Appl. Math. Comput. 217, 4359–4368 (2011)

    Article  Google Scholar 

  • Raptis A.: Flow through a porous medium bounded by a semi-infinite surface. Mech. Res. Commun. 11, 277–279 (1984)

    Article  Google Scholar 

  • Raptis A., Perdikis C.: Unsteady flow through a porous medium in the presence of free convection. Int. Commun. Heat Mass Transf. 12, 697–704 (1985)

    Article  Google Scholar 

  • Raptis A., Takhar H.S.: Flow through a porous medium. Mech. Res. Commun. 14, 327–329 (1987)

    Article  Google Scholar 

  • Ridha A.: Aiding flows non-unique similarity solutions of mixed convection boundary-layer equations. J. Appl. Math. Phys. 47, 341–352 (1996)

    Article  Google Scholar 

  • Sathiyamoorthy M., Basak T., Roy S., Pop I.: Steady natural convection flow in a square cavity filled with a porous medium for linearly heated side wall (s). Int. J. Heat Mass Transf. 50, 1892–1901 (2007)

    Article  Google Scholar 

  • Schlichting H., Gersten K.: Boundary-Layer Theory. Springer, Berlin (2000)

    Google Scholar 

  • Vadasz, P. (eds): Emerging Topics in Heat and Mass Transfer in Porous Media. Springer, New York (2008)

    Google Scholar 

  • Vafai, K. (eds): Handbook of Porous Media (2nd edition). Taylor & Francis, New York (2005)

    Google Scholar 

  • Vafai K.: Porous Media: Applications in Biological Systems and Biotechnology. CRC Press, Boca Raton, FL (2010)

    Book  Google Scholar 

  • Vafai K., Tien C.L.: Boundary and inertia effects on flow and heat transfer in porous media. Int. J. Heat Mass Transf. 24, 195–203 (1981)

    Article  Google Scholar 

  • Weidman P.D., Kubitschek D.G., Davis A.M.J.: The effect of transpiration on self-similar boundary layer flow over moving surface. Int. J. Eng. Sci. 44, 730–737 (2006)

    Article  Google Scholar 

  • Yamamoto K., Iwamura N.: Flow with convective acceleration through a porous medium. J. Eng. Math. 10, 41–54 (1976)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science and Institute for Mathematical Research, Universiti Putra Malaysia, 43400 UPM, Serdang, Selangor, Malaysia

    Haliza Rosali

  2. Centre for Modelling and Data Analysis, School of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, 43600 UKM, Bangi, Selangor, Malaysia

    Anuar Ishak

  3. Faculty of Mathematics, University of Cluj, CP 253, 3400, Cluj, Romania

    Ioan Pop

Authors
  1. Haliza Rosali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Anuar Ishak
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ioan Pop
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ioan Pop.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rosali, H., Ishak, A. & Pop, I. Mixed Convection Stagnation-Point Flow Over a Vertical Plate with Prescribed Heat Flux Embedded in a Porous Medium: Brinkman-Extended Darcy Formulation. Transp Porous Med 90, 709–719 (2011). https://doi.org/10.1007/s11242-011-9809-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11242-011-9809-7

Keywords

Search

Navigation