The lesson of Newcomb’s paradox

Abstract

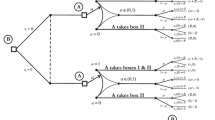
In Newcomb’s paradox you can choose to receive either the contents of a particular closed box, or the contents of both that closed box and another one. Before you choose though, an antagonist uses a prediction algorithm to accurately deduce your choice, and uses that deduction to fill the two boxes. The way they do this guarantees that you made the wrong choice. Newcomb’s paradox is that game theory’s expected utility and dominance principles appear to provide conflicting recommendations for what you should choose. Here we show that the conflicting recommendations assume different probabilistic structures relating your choice and the algorithm’s prediction. This resolves the paradox: the reason there appears to be two conflicting recommendations is that the probabilistic structure relating the problem’s random variables is open to two, conflicting interpretations. We then show that the accuracy of the prediction algorithm in Newcomb’s paradox, the focus of much previous work, is irrelevant. We end by showing that Newcomb’s paradox is time-reversal invariant; both the paradox and its resolution are unchanged if the algorithm makes its ‘prediction’ after you make your choice rather than before.