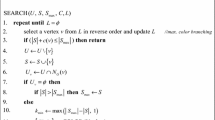iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s11227-006-9157-5
Work-efficient BSR-based parallel algorithms for some fundamental problems in graph theory | The Journal of Supercomputing Skip to main content
Springer Nature Link
Log in

Work-efficient BSR-based parallel algorithms for some fundamental problems in graph theory

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

This paper presents BSR-parallel algorithms for some problems in fundamental graph theory : transitive closure, connected components, spanning tree, bridges and articulation points of a graph and bipartite graph recognition. There already exist constant time algorithms to solve these problems on a mesh with reconfigurable bus system using O(N 4) processors. Here we show that these problems can be solved in constant time using only O(N 2) processors on the BSR model (N is the number of vertices of the graph G). Therefore, our algorithms are more work-efficient. These new results suggest that many other problems in graph theory can be solved in constant time using the BSR model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aho AV, Hopcroft JE, Ullman JD (1974) The design and analysis of computer algorithms. Addison-Wesley, Reading, MA

    MATH  Google Scholar 

  2. Akl SG (1997) Parallel computation: Models and methods, Prentice Hall, Upper Saddle River, NJ

    Google Scholar 

  3. Akl SG, Guenther GR (1989) Broadcasting with selective reduction. In: Information Processing 89, Ritter GX (ed) Proceedings of the IFIP 11th world computer congress. North–Holland, San Francisco, pp 515–520

  4. Akl SG, Stojmenovic I (1994) Multiple criteria BSR: An implementation and applications to computational geometry problems. In: Proceedings of the twenty-seventh annual hawaii international conference on system sciences

  5. Akl SG, Stojmenovic I (1996) Broadcasting with selective reduction: A powerful model of parallel computation. In: AY Zomaya (ed) Parallel and distributed computing handbook. McGraw-Hill, New York, pp 192–222

    Google Scholar 

  6. Arlazarov VL, Dinic EA, Kronrod MA, Faradzev IA (1970) On economical construction of the transitive closure of a directed graph. Soviet Math Dokl 11:1209–1210

    MATH  Google Scholar 

  7. Atallah MJ, Kosaraju SR (1984) Graph problems on a mesh-connected processor array. J Assoc Comput Mach 31(3):649–667

    MATH  MathSciNet  Google Scholar 

  8. Auslander L, Parter SV (1961) On embedding graphs in the plane. J Math Mech 10:517–523

    MATH  MathSciNet  Google Scholar 

  9. Berge C (1962) The theory of graphs and its applications. John Wiley and Sons, New York

    MATH  Google Scholar 

  10. Bollobás B (1979) Graph Theory: An introductory course. Springer Verlag, New York

    Google Scholar 

  11. Bondy JA, Murty USR (1976) Graph theory with applications. Elsevier North-Holland, New York

    Google Scholar 

  12. Delacourt E, Myoupo JF, Semé D (1999) A constant time parallel detection of repetition. Parall Proc Lett 9(1):81–92

    Article  Google Scholar 

  13. Fava Lindon L, Akl SG (1993) An optimal implantation of broadcasting with selective reduction. IEEE Trans Paral Distr Syst 4(3):256–269

    Article  Google Scholar 

  14. Guibas LJ, Kung HT, Thompson CD (1979) Direct VLSI implementation of combinatorial algorithm. In: Proc. Caltech Conference on VLSI, pp 509–525

  15. Huang TS, Tsai MS (1989) A linear systolic algorithm for the connected component problem. BIT 29:217–226

    Article  MATH  MathSciNet  Google Scholar 

  16. Kung SY, Lo SC, Lewis PS (1987) Optimal systolic design for the transitive closure and shortest path problems. IEEE Trans Comput C36(5):603–614

    Google Scholar 

  17. Manber U (1989) Introduction to algorithms: A creative approach. Addison-Wesley

  18. Myoupo JF, Semé D (1997) A parallel solution of the sequence alignment problem using BSR model. In: Proc. of the 10th international conference of parallel and distributed computing systems. pp 357–362

  19. Myoupo JF, Semé D (1999) Time-efficient parallel algorithms for the longest common subsequence and related problems. J Parall Distri Comput 57:212–223

    Article  MATH  Google Scholar 

  20. Myoupo JF, Semé D (2000) Efficient parallel algorithms for the LIS and LCS problems on BSR model using constant number of selections. Parall Alg Appl 14:187–202

    MATH  Google Scholar 

  21. Myoupo JF, Semé D (2002) Optimal BSR solutions to several convex polygon problems. J Supercomput 21(1):77–90

    Article  MATH  Google Scholar 

  22. Ramakrishnan IV, Varman PJ (1984) Dynamic programming and transitive closure on linear pipelines. In: Proc ICPP

  23. Semé D (1999) An efficient algorithm on the BSR-based parallel architecture for the k-LCS problem. In: Proc Int Conf Parall Distr Proc Techn Appl (to appear 1999)

  24. Stojmenovic I (1996) Constant time BSR solutions to parenthesis matching, tree decoding, and tree reconstitution from its traversals. IEEE Trans Parall Distr Syst 7(2):218–224

    Article  Google Scholar 

  25. Wang BF, Chen GH (1990) Constant time algorithms for the transitive closure and some related graph problems on processor arrays with reconfigurable bus systems. IEEE Trans Parall Distr Syst 1(4):500–507

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire de Recherche en Informatique d’Amiens (LaRIA), Université de Picardie Jules Verne, Faculté de Mathématiques et d’Informatique, 33 rue Saint-Leu, 80039, Amiens Cedex 1, France

    Jean-Frédéric Myoupo & David Semé

Authors
  1. Jean-Frédéric Myoupo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David Semé
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jean-Frédéric Myoupo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Myoupo, JF., Semé, D. Work-efficient BSR-based parallel algorithms for some fundamental problems in graph theory. J Supercomput 38, 83–107 (2006). https://doi.org/10.1007/s11227-006-9157-5

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-006-9157-5

Keywords

Search

Navigation