Abstract
The Information Security Management Systems (ISMS) are global and risk-driven processes that allow companies to develop their cybersecurity strategy by defining security policies, valuable assets, controls, and technologies for protecting their systems and information from threats and vulnerabilities. Despite the implementation of such management infrastructures, incidents or security breaches happen. Each incident has associated a level of severity and a set of mitigation controls, so in order to restore the ISMS, the appropriate set of controls to mitigate their damage must be selected. The time in which the ISMS is restored is a critical aspect. In this sense, classic solutions are efficient in resolving scenarios with a moderate number of incidents in a reasonable time, but the response time increases exponentially as the number of incidents increases. This makes classical solutions unsuitable for real scenarios in which a large number of incidents are handled and even less appropriate for scenarios in which security management is offered as a service to several companies. This paper proposes a solution to the incident response problem that acts in a minimal amount of time for real scenarios in which a large number of incidents are handled. It applies quantum computing, as a novel approach that is being successfully applied to real problems, which allows us to obtain solutions in a constant time regardless of the number of incidents handled. To validate the applicability and efficiency of our proposal, it has been applied to real cases using our framework (MARISMA).
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Concepts such as cybersecurity and cyberdefense are becoming increasingly present in a society dominated by the digital technology (Dashti et al., 2017; Bongiovanni, 2019; Eslamkhah & Hosseini Seno, 2019). In fact, in an ever-changing world, where digitization reaches all areas, cybersecurity issues are one of the main threats to the privacy of individuals, to the sustainability of companies, and to the protection of their assets (Mortazavi & Safi-Esfahani, 2019). As a result, some authors stress that organizations have to cope with increased risk due to threats to their Information and Communication Technologies (ICT), which compromises their very survival (Gritzalis et al., 2018). In this context, data and information systems are critical assets that need to be adequately protected (Szabó, 2017; Yoseviano & Retnowardhani, 2018), but this is nevertheless a complex objective to fulfill (Akinwumi et al., 2018), requiring a clear commitment and awareness on the part of organizations (Sardjono & Cholik, 2018; Ahmad et al., 2021) and personal and financial resources that in most cases are not available (Mortazavi & Safi-Esfahani, 2019).
According to the ISO/IEC 27.001, the Information Security Management System (ISMS) is part of an overall management structure focused on preserving the information security within organizations. This management structure includes the definition of security policies and procedures that imply people, processes, and technology for its alignment with the business strategy. To be effective, the implementation of an ISMS needs a considerable resources investment (Ahmed & Nibouche, 2018) and a detailed plan defining how to respond against security incidents (Proença & Borbinha, 2018). In fact, a key element of each ISMS is the security risk assessment and management strategy (Hariyanti et al., 2018; Szwaczyk et al., 2018; Ruan, 2017; Alshawabkeh et al., 2019), but security risks do not only affect to ICT components of organizations, but also their business processes, and even the organization and strategy level (Ross et al., 2019). Therefore, effective risk management helps top managers to make optimal decisions (Tiganoaia et al., 2019; Wolf & Serpanos, 2020), as security incidents can have harsh consequences to different levels of the organization (Debnath et al., 2020).
Currently, risk assessment and management solutions have numerous open issues that complicate their applicability and effectiveness. First of all, most security incidents are caused by the general lack of awareness of risk or their inaccurate assessment (Turskis et al., 2019). In addition, the natural state of risks is dynamic, as they are related to constantly evolving threats and vulnerabilities, but unfortunately mainstream approaches provide a static picture of risks (Paltrinieri & Reniers, 2017). Moreover, existing risk assessment methods rely heavily on the experience of risk experts (Sun & Xie, 2019), so new methods that exploit knowledge reuse are needed to provide effective and objective risk management and limit the assumed costs (Alhawari et al., 2012). In this scenario, cybersecurity incidents are on the rise, both in intensity and impact (Glantz et al., 2017), so the scientific community is calling for the development of appropriate methodologies and tools to enable companies to address, understand and manage their cybersecurity risk, improving their current drawbacks (Thakur et al., 2015; Wang et al., 2018).
However, the aim of this paper is to try to contribute to the resolution of a specific problem of security incident response, which is a fundamental aspect of ISMS and in particular is a part of risk management, and which is responsible for reacting to incidents by applying controls to reduce damage and efficiently restore systems (Bhardwaj & Sapra, 2021). The problem we address is how to find and select the minimum set of incidents that we must undertake to cover all existing controls involved in a given period of time, taking into account the severity of these incidents and the set of controls that have been affected by them. Thus, in the normal production operation of an information system, a large daily volume of security incidents may occur on a daily basis and need to be reviewed and corrected. Moreover, these incidents are not isolated from each other, but in many cases, we can find interdependencies, so that several security events can affect the same security controls. For example, we can have a baseline scenario with 4 unresolved incidents that globally affect 2 security controls. In this way, by optimizing the set of incidents to be resolved, it is possible that resources need only be allocated to two of the incidents, with the other two being resolved directly after the corresponding controls have been reinforced, thus saving time and resources. This is an optimization problem that is easily solved with traditional algorithms when the number of incidents and associated controls is small, but as the number of incidents increases, the problem becomes unsolvable from a traditional perspective, because the algorithm complexity is exponential and therefore, we must find other approaches. In this paper we explore another paradigm to solve this problem, quantum algorithms.
In fact, although quantum computing is in its most incipient stages, it has already left the research stage and is ready for industrial use, making it a prime candidate for solving certain types of highly complex problems for which even supercomputers are failing (Mueck, 2017). In particular, this new paradigm is already being applied to solve certain types of problems for which such a computing paradigm is particularly suitable (Hidary, 2019), such as optimization (Lucas, 2014) or machine learning problems (Wittek, 2014), which are widely used today. Moreover, the emergence of these new quantum computers, has a great implication in computer security, due to the weakness of cryptographic systems against the computational power of quantum systems (Shor, 2002) and the need for the emergence of a new post-quantum cryptography (Mailloux et al., 2016). In particular, the problem proposed in this paper concerns the optimization of incident response in a risk analysis and management system, where incident response can be optimized by selecting those appropriate controls to perform, being a problem that grows exponentially with the number of incidents. For this reason, and given that the optimization of the response may not converge in a classical computer, a solution based on a quantum annealing algorithm has been proposed to find the optimal configuration to the problem. This solution has been successfully programmed and tested on a D-Wave quantum computer.Footnote 1
In previous works we have developed MARISMA (Rosado et al., 2021), a comprehensive and extensible framework that is being applied to carry out risk assessment and management for many and different companies, and which addresses most of the drawbacks of current approaches. Through our experience applying our framework to real cases, we have identified this problem in the security incident response process. Thanks to this framework, we were able to validate the proposed quantum algorithm on real cases.
The article continues in Section 2 by analyzing the background and some related work of security incidents and quantum optimization; Section 3 shows the approach we follow in MARISMA to manage the response to security incidents; Section 4 presents the algorithm proposed by quantum programming to solve the problem posed, and shows an analysis and comparison of the results obtained by applying the quantum algorithm versus the classical algorithm; finally, Section 5 shows the main conclusions obtained during the research and future work to be carried out.
2 Background and related work
This section includes background content about the three research topics addressed in this paper, quantum programming, quantum optimization and security incident response. In particular, the first subsection discusses the foundation on which quantum computing is based, and the second subsection presents how this programming paradigm can be applied to optimization problems. In the third subsection, we provide an overview of the security incident response process and discuss some open research problems.
2.1 Quantum programming
Quantum computing, a paradigm that exploits the quantum physical aspects of reality, promises to have a huge impact in computing (IBM: The Quantum Decade, 2021). However, to have real applications of quantum computing, programming languages are needed that provide structured and high-level descriptions of quantum algorithms, without reference to the underlying hardware (Clairambault et al., 2019).
The discovery of efficient quantum algorithms by Shor (2002) and Grover (1997) has sparked a lot of interest in the field of quantum programming. However, it remains a very difficult task to find new quantum algorithms mainly because quantum programs are very low-level due to they are usually represented as quantum circuits, or in some combinator language that results in functional circuits (Altenkirch & Grattage, 2005). The first aspect that distinguishes quantum programming from classical programming is the use of quantum bits (qubits) instead of bits (Sánchez & Alonso, 2021).
The way in which quantum programmers work with qubits is through quantum circuits and quantum gates. Computation in quantum programming is performed, under the circuit representation of quantum programs (QP), by means of gates, which provide the primitive operations to manipulate the magnitude and phase of the system qubits (Sánchez & Alonso, 2021). Quantum circuits and gates can be represented graphically like in Fig. 1, but also through syntax-based notations that are provided by a wide variety of quantum programming languages (e.g., Q#, QASM, Cirq, pyquil, QCL, among many other) which have been proposed to make it easier to specify quantum algorithms. These quantum algorithms are usually a translation of the quantum circuit into code, i.e., a sequence of textual programming statements.
Since the first practical quantum programming language QCL was introduced, many other languages have appeared (Heim et al., 2020), some of them more oriented to quantum circuits (like the “classical” assembler), while others are closer to high-level languages. The design of subsequent quantum programming languages was influenced by the QRAM (quantum random access machine) model (Knill, 1996) in which the quantum system is controlled by a classical computer. Various quantum programming languages have been released in the last few years including LIQUi|⟩ (Wecker & Svore, 2014), Quipper (Green et al., 2013), Scaffold (Abhari et al., 2012), and, more recently, Q# (Svore et al., 2018) or Q|SI⟩ (Liu et al., 2018). All of these languages propose answers to the fundamental questions of quantum programming and were designed with the aim of addressing the challenges of practical quantum computing. In particular, all of these languages make it possible to express and reason about quantum algorithms of the size and type expected in real-world applications of quantum computing. In doing so, quantum programming environments can play an essential role in turning quantum computers from objects of science into instruments of scientific discovery (Gyongyosi & Imre, 2019).
Many quantum programming languages have been designed and implemented in terms of different types of language paradigms for programming quantum computers (Zhao, 2020). A first and major semantic distinction is between imperative and functional languages. Imperative languages are described by specifying how the execution of a given program modifies a global state. On the other hand, programs in functional languages map inputs to outputs, and more complex programs are built out of elementary function (Heim et al., 2020). Nowadays, the main imperative quantum programming languages are Q# (Svore et al., 2018), Q|SI⟩ (Liu et al., 2018), ProjectQ (Steiger et al., 2018) and Qiskit (Aleksandrowicz et al., 2019), among others. As concerns functional languages, there are not too many proposals, but we can find Quantum lambda calculi (Maymin, 1996), Quipper (Green et al., 2013), LIQUi|⟩ (Wecker & Svore, 2014) among the principal contributions. Finally, we can highlight qASM (Pakin, 2016) and Quil (Smith et al., 2016) for other quantum programming languages paradigms.
2.2 Quantum optimization
Quantum computing technology offers fundamentally different solutions to computational problems and enables more efficient problem solving than is possible with classical computations (Gyongyosi & Imre, 2019).
A qubit is usually represented with the electron spin or photons among other subatomic particles. A qubit is a multiple status quantum system, i.e., it is not only defined by zero or one as a classical bit, but possible values exist at the same time. So, a qubit can be zero or one with a certain probability (this is known as superposition and is the key for the high computational power). The actual value of a qubit is only known once it is measured, and then, the qubit is collapsed and cannot be used anymore without resetting. As a result, the philosophy of quantum programming is oriented toward exploring and searching optimal solutions in a probabilistic space (Piattini et al., 2021).
Many of the quantum optimization algorithms are based on search algorithms using the well-known Grover’s (1997) algorithm, which performs a search in an unknown search space based on encoding the solution requirements by means of a quantum oracle. These quantum oracles (Sutor, 2019; Johnston et al., 2019), are a sort of black box that can be assimilated to the function concept of high-level languages and that help in the construction of these search algorithms with linear complexity.
In addition, other quantum environments such as Quantum Leap from quantum computer manufacturer D-WaveFootnote 2 provide optimization environments for NP-hard combinatorial problems using adiabatic quantum optimization (Farhi et al., 2001; Das & Chakrabarti, 2008). This type of programming is based on the specification of the system to be optimized as a Hamiltonian that represents both the objective and the constraints of the system and the quantum computer is responsible for finding the solution that provides the lowest energy to the system. Some approaches to this quantum optimization system based on Ising expressions can be found in Lucas (2014). There are also alternatives based on programming based on quantum gates, such as the one found in the Qiskit textbook (Asfaw et al., 2020), which implements the quantum approximate optimization algorithm (QAOA) (Farhi et al., 2014).
Quantum adiabatic computing is a great step forward in the path of optimization algorithms, in which apart from the classical search algorithms (with several limitations in efficiency and effectiveness), such as backtracking, dynamic programming, heuristic search such as A* or adversarial search, such as Minimax or branch and bound algorithms, new algorithms and approaches have been identified and developed that have been gradually improving the efficiency of this type of techniques. Among the recent improvements in these algorithms, we could highlight the genetic algorithms (Rocke, 2000), the classical annealers such as the simulated annealing algorithms (Kirkpatrick et al., 1983) or benchmark functions algorithms (Dieterich & Hartke, 2012). However, all these solutions usually have limitations when working with local minimums and do not usually give good results when dealing with really large or complex problems. In this sense, adiabatic quantum computation is probably one of the great promises in solving complex optimization NP-complete problems in polynomial time (Černý, 1993).
The usual process of quantum annealing algorithms is to specify the problem to be solved as qubits in a superposition state and through the annealing process collapse the qubits to a classical state that is either 0 or 1 and represents the lowest energy solution to the proposed problem. As can be seen in Fig. 2 the process starts with an energy state that corresponds to the superposition state of the qubits, in which there is only one valley (a), as the annealing process progresses the energy possibilities are separated generating a double-well potential state (b). At the end of the process one of the valleys corresponds to the minimum energy that stabilizes the system and a deeper valley corresponding to that solution is generated (c).Footnote 3
In our work we apply a quantum computing approach to optimize incident response management in the context of a risk assessment and management framework. This quantum computing approach will specify incidents with their associated threats and controls and search for the minimum energy state that represents the best solution for incident resolution in the shortest possible time.
2.3 Managing security incidents
As mentioned in Section 1, security incidents are undesired events that impact the different dimensions of the valuable assets that make up a company’s information systems (Mahima, 2021). These incidents are caused by failures in the implementation of the security controls that protect these assets, i.e., by vulnerabilities that exist in the information systems. These vulnerabilities are exploited by threats to reach these assets and cause damage to them (Dion, 2020).
In order to minimize the damage of these incidents, organizations try to apply the most appropriate incident response methods (Prasad & Rohokale, 2020). In fact, the management of security incidents and the correlation of these events is a topic of great interest to the scientific community (Salvi et al., 2022). Many organizations have focused on managing risks through integrated services in Computer Security Incident Response Teams (CSIRT), as these have proven to be one of the best solutions to improve cybersecurity by collaborating with each other, sharing knowledge and learning from cross experiences (Tanczer et al., 2018). However, the implementation of a CSIRT comes at a considerable cost, which makes it only suitable for large organizations, with the need to create simpler and more effective incident management systems for small and medium-sized enterprises (Pleta et al., 2020).
Security incident management and response can be considered a hot research topic with some relevant open questions (Grispos et al., 2017). One of the most relevant question is how to achieve a reasonable situational awareness to know the situation regarding vulnerabilities, threats and possible security incidents (Ahmad et al., 2021). In this area, there is recent intense research, for example proposing models to explain how organizations should achieve situational awareness of cybersecurity (Ahmad et al., 2020), arguing that providing a rapid and efficient response to security incidents clearly supports cybersecurity awareness and improves the overall cybersecurity performance of companies (Naseer et al., 2021), or considering misinformation as one of the key reasons for the lack of situational awareness (Ahmad et al., 2019). Indeed, it is often claimed that attackers take advantage of the lack of corporate communication following cybersecurity incidents (Knight & Nurse, 2020) and the lack of learning from their experiences in incidents (Ahmad et al., 2020, 2015, 2012).
It is, therefore, necessary for any type of company to have adequate and efficient tools to support incident management processes. And above all, utilities and processes provide them with mechanisms that facilitate decision-making to optimize the selection and prioritization of security incidents to be resolved (Ahmad et al., 2015). This is mainly due to the fact that the incidence workload can be very high throughout the lifecycle of an information system, especially in typical cases such as the release of a new version of an application or an operating system upgrade. Thus, there is a strong need to take into account the specific efficiency and effectiveness needs of these new incident management support systems (van der Kleij et al., 2021).
But for us, in this work, the most relevant problem faced by organizations is agility in managing and responding to security incidents (Tam et al., 2021). This agility translates into the need to respond to these incidents in the shortest possible time (van der Kleij et al., 2021; He et al., 2022). But this problem is becoming increasingly difficult to address, due to the growing number of incidents and their interconnection. When systems receive hundreds of events, we find that incident response teams must make a decision on which are the top incidents to start analyzing. In this sense, a key factor in organizing and prioritizing the incidents to be resolved is the possible relationships between them. An information system has different security controls dedicated to protect the system’s assets against potential threats, or even to fix vulnerabilities inherent to certain assets (such as software or operating systems). Thus, the most common scenario is that several reported incidents affect the same set of controls. The correct selection of the controls to be strengthened may therefore mean that resolving a single incident automatically resolves several related incidents. Consequently, by appropriately prioritizing the resolution of incidents, it is possible to optimize both the use of resources and the time spent in the overall process. But this prioritization cannot be done manually, as it would delay decision-making. According to some researchers, security incident response requires complex event processing (to capture, process, integrate and analyze data in real time), as well as investigation of the cause-effect relationship between incidents (Naseer et al., 2021).
Therefore, we can see how most of the current research related to security incidents has concluded that agility in responding to security incidents is the basis for the correct management of an information system (Aoyama et al., 2020). But very little research has focused on solving the problems arising from the computational complexity of having to analyze large numbers of events in short periods of time, also taking into account the possible relationships between the different security incidents to be solved. And it is this agility in analysis that will allow the right decisions to be made in reasonable timeframes (Srinivas et al., 2019).
3 MARISMA framework for managing security risks and incidents
In this section we present the MARISMA framework (Rosado et al., 2021), our approach to dynamic risk analysis and management. We begin by presenting the aim and the main components of this framework, and then we detail the process we carry out for the management of security incidents and the subsequent processing of these incidents to generate useful knowledge that helps in the company’s decision-making, ending by showing the computational limitations that currently prevent its efficient use.
3.1 MARISMA architecture
MARISMA is our risk analysis and management framework, which we have been developing, improving, extending and applying to many types of companies and technologies over the last decade. As can be seen in Fig. 3, the framework consists of three parts, a methodology supported by a metadata structure, an extensibility mechanism and an automatic tool that supports the methodology and implements the extensions.
The core element of our framework is a methodology that sets out a comprehensive and detailed process for carrying out the entire risk assessment and management lifecycle for an enterprise or part of it, including the necessary activities to configure the appropriate reusable data structures to be used, the semi-automatic generation of risk data and, finally, the dynamic risk management, which includes specific tasks for security incident response. The methodology is supported by a set of Key Risk Indicators (KRI) and by a metadata structure (the Risk Meta-Pattern in Fig. 3), which defines the components and their relationships that allow for maximum customization and automation of the risk assessment and management process. But being aware that different sectors or different technological environments may need a different risk assessment and management strategy (e.g., being affected by different types of threats, or for having assets of different nature), or even that risk may be considered at different abstraction level (e.g., information systems risks or business processes risks), we offer the possibility to instantiate our metadata structure in specific contexts (our Specific Patterns in Fig. 3), such as the ISO/IEC 27.001, Big-Data based systems, Cyber-Physical Systems (CPS), and Business Processes.
The last component of our framework is the e-MARISMA tool, which was developed considering a Software as a Service architecture in the Cloud and using Java stack technology. This tool implements all the processes of the methodology and it is possible to configure it to support any pattern representing a particular context. It offers a rich set of services, not only related to the pattern configuration and administration, but also focused on the risk assessment and management processes carried out by our customers. The main objective of this tool is to be able to perform fast, cheap, visual, and accurate risk assessment, as well as efficient and effective risk management, so we exploit reusability as much as possible. In addition, the tool learns from the knowledge gathered from the occurrence of security incidents, and consequently can make automated decisions by correlating incidents.
This framework has been applied to different types of companies (electric, hydrocarbons, governments, health, shipbuilding, chemical industry, etc.) in more than eight European and Latin American countries.
3.2 Incident response in MARISMA
As mentioned in the previous section, the security incident management and response is a critical activity carried out within the dynamic risk management process of our framework. Once an incident is identified, we need to collect, categorize and analyze the incident context information, and some relevant parameters need to be adjusted in our system (level of risks and compliance controls, involved controls, probability of threat occurrence, etc.). This parameter turning depends on the set of concepts and relationships defined in our risk meta-pattern, and on its specific instantiation through one pattern, which will include the components selected through the process shown in Fig. 4, and which are formally defined in Definition 1.
Definition 1
A Security Incident for MARISMA. Let \(si_i\) be a security incident. Together with \(si_i\), the tuple \(\langle T,AG,A,RD,C \rangle\), as additional information is defined, where T represents a set of n threat types {\(t_1\), \(t_2\), \(\ldots\), \(t_n\)} that have caused the security incident, AG is a set of m asset groups {\(ag_1\), \(ag_2\), \(\ldots\), \(ag_m\)} affected by these threats. Each asset type is related to A, a set of l assets {\(a_1\), \(a_2\), \(\ldots\), \(a_l\)}, and each asset has associated RD, a set of k risk dimension {\(rd_1\), \(rd_2\), \(\ldots\), \(rd_k\)}. Finally, each group of assets is affected by the failure of C, a set of j control {\(c_1\), \(c_2\), \(\ldots\), \(c_j\)}.
This process is fully implemented by eMARISMA, which provides a workflow to (i) enter the security incident information (a description, the cause, the responsible person, and the time limits to be solved), (ii) select from the stored information and according to the data relationships defined by the risk pattern the hierarchy of elements that are involved with the security incident (threats, assets and controls), defining other related information such as the severity of the incident, and quarantine the affected controls by temporarily lowering their coverage level while the incident is resolved, and finally, once the incident is solved, (iii) support knowledge management and learning from the security incidents occurred by recording the lesson learned, incident resolution costs and some concluding remarks. Obviously, when a security incident occurs and is recorded, a set of chain changes are automatically applied on the risk components according to the stored meta-information. This is because the level of compliance with security controls is penalized if a threat has compromised the control, which affects the risk level of many other assets, and which implies that those controls need to be reviewed and strengthened.
However, a typical scenario in incident management is the heavy workload involved in organizing and prioritizing incidents in order to define the most efficient way to resolve them in the shortest possible time and using available resources appropriately. The organization and efficient distribution of incidents becomes even more complicated at peak activity, such as the first production start-up of a system or the registration of a new service, when the number of incidents can reach large amounts, with the added complication of managing them properly. Thus, it is common to have to prioritize and plan dozens (or even hundreds) of incidents in a short period of time, which involves complex calculations, a high level of difficulty, and a high cost in time. This scenario is further complicated by the fact that incidents are not usually isolated elements, but are often related to each other to a greater or lesser extent, so the order of incident resolution is important to address problems in an optimized way. It is therefore important to have systems that are capable of managing these large volumes of security incidents in order to obtain the best action plans.
To illustrate this problem, we will consider this example based on a typical dataset of reported incidents to be treated according to the incident management structure used by eMARISMA (see Table 1), which defines the following attributes: (i) IdIncident: Unique identifier of the incident, (ii) IdThreat: Threat code according to the definition of the pattern used, (iii) Threat: Description of the threat that has caused the incident, (iv) Severity: Qualitative assessment of the severity of the incident (between 1 and 5), (v) IdControl: Control code according to the definition of the pattern used, (vi) Control: Description of the control that has been affected by the threat, and (vii) Estimated Time: Estimate of number of hours required to resolve the incident.
As we can see in Table 1, we consider that each incident involves a single threat, which is usually the most frequent scenario. Each incident may affect one or more controls whose implementation must be reviewed and corrected to resolve the incident and try to prevent its recurring. In addition, it is common for several incidents to be related to the same control. For example, control [12.1.3] Capacity management has been affected by both security incidents 1 and 6. Similarly, we can see how control [12.3.1] Information backups is affected by incidents 1 and 9. In this way, by prioritizing the resolution of incident 1, we reinforce the two affected controls, and incidents 6 and 9 would also be resolved, with the consequent savings in time and resources.
This optimization problem, which consists of selecting the minimum set of incidents from among those identified that cover the entire set of affected controls, is easy to solve by means of adequate planning for small sets of incidents, but becomes enormously complicated when working with volumes of hundreds of incidents, requiring a large amount of time and resulting in planning that is not very efficient in many cases. In this sense, quantum computing emerges as a powerful mechanism to solve this identified problem.
4 Quantum algorithm for incident response optimization
In this section, we first show the algorithmic solution proposed for the problem posed, using quantum algorithms, and after that, we compare the results obtained using classical algorithms versus the proposed solution using quantum algorithms.
4.1 Algorithm definitions
In order to correctly plan the algorithmic solution of the proposed problem, it is necessary to specify the variables and entities that are part of the algorithm. These variables can be defined as follows:
Definition 2
Let be i a unique identifier of an incident corresponding with the IdIncident of Table 1.
Definition 3
Let be k a control identifier representing the IdControl unique control code.
Definition 4
Let be C\(_k\) the set of incidents related to IdControl k.
Definition 5
Let be t\(_i\) the estimated time in hours necessary for solving the incident whose IdIncident is equal to i, mapping to the Time value.
Definition 6
Let be x\(_i\) a binary variable that determines, at the algorithm solution, whether the incident i is selected to be addressed.
Definition 7
Let be P a penalty coefficient, which serves to modulate the weight of the constraints in the algortihm definition. It can be found empirically to be equal to the highest estimated time among all the occurrences plus 1, thus affecting the whole solution.
Based on these definitions we can express algebraically the objective pursued by executing the quantum optimization algorithm that will be sent to the quantum computer.
4.2 Algorithm approach
As we can observe in Section 3, the present problem is a variation of the Minimum Vertex Cover algorithm,Footnote 4 in which the input to the algorithm is a series of incidents identified by their ID. Each of the incidents has a severity and an estimated resolution time. In addition, it has a series of associated controls that will have to be reviewed and strengthened in order to consider that the incident has been resolved. These controls can be associated to the resolution of several incidents, so that if we resolve an incident that shares controls with another one, we resolve that for other incident at the same time. To solve the problem, we should select a result in which the minimum set of incidents to be solved is selected, so that we cover all the controls that allow us to solve the other incidents. This solution must be done in the shortest possible time.
As discussed in Section 2, for solving this kind of problems, there are several good approaches such as genetic algorithms or classical annealers but the lack the ability to solve complex optimization problems in polynomial time. Regarding solutions based on quantum computation, we have basically two main options, quantum gate-based circuits and adiabatic quantum algorithms. While it is true that some approaches based on quantum gates, such as the QAOA algorithm, allow the resolution of optimization problems with an approximation similar to quantum annealers, its formulation and, above all, its implementation as a quantum circuit is much more complex and extensive than the formulation of the Hamiltonian of quantum annealers and its representation as Ising or QUBO, which are much simpler to understand and independent of the underlying quantum platform.
In order to solve the problem, we will model this problem as a Quadratic Unconstrained Binary Optimization (QUBO) problem, also known as unconstrained binary quadratic programming (UBQP), which will represent the objectives and constraints of our problem and can be sent to the solver of the adiabatic quantum computer to find the minimum energy state, which will coincide with the combination of variables, i.e., incidents, that must be selected to find an optimal result to our problem.
All optimization problems following the QUBO pattern are specified on the basis of a Hamiltonian, which in the form of a summation indicates the objective and the constraints to be met by the solution. This Hamiltonian is expressed as a Binary Quadratic Model (BQM) and is converted into a BQM matrix which is the one we will pass to the adiabatic solver.
Our main objective is to minimize the total time of the issues that are part of the solution. In the form of a BQM expression we could specify it as follows:
Being \(x_i\) the binary variable that determines whether or not the incident i is selected, and \(t_i\) the estimated time related to the incident i. It should be noted that our goal is to minimize this objective.
The constraints are somewhat more complicated to model, since the incidents can be fulfilled either because they have been selected, or because the set of controls that form part of it have already been solved by one or more previously selected issues. A possible solution could be to make a graph that relates all the incidents that share controls and to select a node from each of the subgraphs. Unfortunately, this solution would only work if the relationships between incidents and controls were one-to-one. In a real case, several controls must be necessary to resolve an incident and therefore, a simple graph is not able to represent such information. If we wanted to extend such a graph to represent the complexity of the relationships between controls and incidents, such a graph would be unmanageable and would not be useful for solving the problem. Therefore, it is necessary to take a new approach, as stated next.
In order to find a possible solution, let’s analyze a small example in Table 2:
In Table 2 we can see that to solve our problem it is not necessary to solve all the incidents {A,B,C} since by attending to a subset of them, e.g., {A,B}, we cover all the necessary controls.
Looking at this small example of Table 2 we can see that building a node that represents all the dependencies between incidents and controls is not easy, because the need of controls for each of the incidents is not the same for each of them, so the graph would be too complicated and should represent 2 types of edges, those representing dependencies between controls and incidents and those representing relationships between incident controls and also these relationships would be partial.
Therefore, the resolution of this problem by means of a network of this type is not a good approximation and we will have to model the restrictions in another way. The solution is to focus on the controls and see how all the incidents are solved through the completeness of the necessary controls.
In this problem, we are looking for all the incidents to be solved, and to determine that an incident is solved we look at whether its controls have been selected or not. In other words, we want all controls to have at least one incident related to it that has been selected. If all the controls have been solved, we know that all the issues will be solved as well. This constraint will be formulated as follows:
Where \(C_k\) is the set of incidents related to the control k. With this expression we control that at least one of the incidents related to k has been selected. Doing this for all the controls, we obtain:
In order to construct the final QUBO equation we need to add a penalty coefficient (P), which serves to modulate the weight of the constraints in the Hamiltonian expression. Empirically, it can be calculated that this coefficient P is the highest estimated time among all the occurrences plus 1, so that the penalty still affects the solution. The final QUBO equation is as follows:
Simplifying the part of the expression that represents the restrictions, we can obtain the following expression:
Considering that x can only take as values 0 and 1, we can eliminate the square it has since it is irrelevant; as well as that of 1:
Simplifying:
We can eliminate the constant part, since it does not modify the solution:
So our BQM (QUBO) expression of the initial Hamiltonian is finally as follows:
The final equation gives us a linear part \((-Px_i)\) and a quadratic part \((2Px_ix_j)\), which will be sent to the quantum annealing solver through a bidimensional matrix generated from the above expression.
Based on the definition of the previous Hamiltonian, the Python code shown in Listing 1 is generated, in which a QUBO matrix is filled in to be sent to the quantum sampler annealing. This algorithm creates a superior triangular matrix, which defines the QUBO matrix for the Binary Quadratic Model (BQM) of the previous Hamiltonian.

4.3 Quantum algorithm execution
Using the code shown in Listing 1, which generates the input matrix for the quantum annealer sampler, we tested the algorithm with a small real example, as shown in Table 3. Using the Listing 1 we generated the triangular QUBO matrix Q, and we send it to the sampler with the code shown in Listing 2

After executing the coding, we get the results of the sampling as a text file in which we can observe the results of the algorithm and the energy of each of the found solutions. The solution with a minimum energy level is the one that fulfills the requirements and goals of our problem. The output of the algorithm for the data shown in Table 3 is shown next:

The output can also be seen graphically as Fig. 5 shows the configuration of the qubits in the quantum processor, in which each of the points shows a qubit representing, respectively, the incidents to be managed. The lines of the generated graph that link the qubits are the constraints and control associations that exist between different incidents. In the same graph, the final configuration of the amplitudes (0 or 1) of each qubit is shown, so that the system remains in the lowest energy configuration.
Figure 6 shows graphically the output of the algorithm in which we can see that incidents [3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15] were selected for being processed, as the controls used for addressing incident number 6 solve also incidents 1 and 9, as occurs with incidents 12 and 8 and also with incidents 4 and 2.
In Fig. 7, the histogram of the energies of the returned examples can be observed. In this figure you can see the occurrence of each of the solutions found by the quantum processor and its associated energy, so that it can be seen visually that the result returned by the algorithm is the final configuration of the qubit states with the lowest energy and that has occurred a greater number of times in the Quantum annealing process. In this case, the best solution was found with an energy value of -100 and it was also the most repeated solution found.
4.4 Empirical results
The classical algorithms that solve this type of problem are usually based on backtracking, dynamic programming or branch and bound, which have an exponential computational complexity. However, adiabatic optimization algorithms, due to their quantum nature and thanks to the concept of superposition, achieve processing similar to multithreaded processing in constant or linear time, depending on the algorithm implemented.
In order to see the computational improvement of the proposed algorithm, we run the algorithm with sample sets of different sizes using a D-Wave 2000Q lower-noise system, with a quantum processor DW_2000Q_6 providing 2048 qubits in a [16,16,4] chimera topology. We also test a classic Backtracking algorithm written in Python running on Mac OS System, with a 3.2 GHz Intel Core i7 and 64 GB DDR4 RAM. As can be seen in Table 4, we observed, in the experiments carried out, a real behavior similar to the expected one, with a constant time and independent of the number of incidents to process (around 3 s), while the time of a backtracking algorithm to solve the problem grows exponentially with the number of incidents, not even converging with one hundred incidents.
In the light of these results we can consider it appropriate to believe that the adiabatic quantum approach for solving optimization problems in the context of security incident management is widely efficient and an improvement over previous management based on classical optimization algorithms.
4.5 Economic considerations
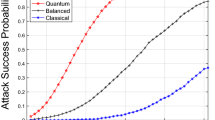
As can be seen in Fig. 8, from 25 security incidents that are interrelated by means of the controls, classical computers are no longer efficient in solving the problem and start to take an increasing amount of time to solve. Between 25 and 40 events, classical systems may still be able to solve the problem, albeit with increasing machine consumption. From 40 events onwards, the complexity of the problem is so high that the problem cannot be solved by classical computers and quantum computing must be used.
But another question we must ask ourselves is when it would become profitable from a cost point of view, taking into account current prices. For this purpose, a cost study has been carried out:
-
Currently according to the Quantum Computing Report (AndreSaraiva, 2022), each qubit-second costs approximately $0.05 USD currently (June 2022).
-
On the other hand, the power consumption of a 3.2 GHz Intel Core i7 processor is around 205W/hour (Cutress, 2021).
-
The estimated cost of energy in Europe in 2022 was 0.3071$ kWh (EuroStat, 2022)
Therefore, the cost will be:
-
From the quantum computer, only 15 qubits have been used. Therefore, the cost has been:
$$\begin{aligned} \begin{aligned}&(0.05 \$Q/sc \times 15 Q) = 0.75 \$Q/sc \\&\$ = United\;Stated\;Dolar; \;Sc = Seconds; Q = Qbits \end{aligned} \end{aligned}$$(10) -
For the traditional computer it has been:
$$\begin{aligned} \begin{aligned}&(205Wh \times 0.0003071\$Wh)/60sc = 0.00104926 \$Ws \\&Wh = Watts/hour; \;\$Wh = USD \times Watss/hour \\&Ws = Watts/seconds;\; \$Ws = USD \times Watss/seconds \\&Sc = Seconds \end{aligned} \end{aligned}$$(11)
If we apply these costs to the results of Table 4, we can see that in this case the economic equilibrium is obtained in the interval between 30 and 40 incidents. From this point onwards, the cost skyrockets for traditional computers. It cannot be calculated from 100 incidents onwards, as the complexity prevents it from finding a solution, and even if it were to find one, its cost would be much higher than the use of a quantum computer Table 5.
Therefore, we can see how quantum computing, in addition to allowing us to solve problems in less time, also allows us to do so at a lower cost. On the other hand, it is expected that the costs associated with quantum computing will continue to fall in the future at a faster rate than those of traditional computers, which will make its use to solve complex problems, such as the one discussed in this article, increasingly efficient Fig. 9.
5 Conclusions
In recent years, security management, risk analysis and, in particular, risk management based on the correct management and learning from security incidents have become increasingly important.
In this regard, the time it takes to respond to incidents and re-establish system security is a crucial aspect. However, the response time offered by classic solutions grows exponentially as the number of incidents increases, making them unsuitable for real-world scenarios.
Our risk analysis and management framework MARISMA, through the use of the automated and cloud-based tool eMARISMA, has allowed us to identify this need through its application to a high number of companies analyzing their risks, and we have realized that this was a major limitation to be able to offer increasing value for these companies, so the need arose to look for solutions that were outside of traditional technologies.
We have designed and implemented an algorithm based on the new paradigm of quantum programming, and after performing a complete set of tests and executions, we can conclude that its results are correct, and as expected according to the nature of the basis of quantum, the execution time obtained is very efficient. Thus, we have shown how this quantum algorithm solves this problem in almost constant time, while classical algorithms offer exponential time cost.
Therefore, we can state that although today there are numerous open problems related to security incident management, especially when dealing with large volumes of data, some of them can be solved using quantum algorithms. In fact, part of our future work is to further investigate quantum algorithms and swarm intelligence applied to the exploitation of our security dataset of security risks and incidents from many organizations, in order to correlate security incidents in real time, providing a global and much more efficient way of responding against security incidents.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Abhari, A. J., Faruque, A., Dousti, M. J., Svec, L., Catu, O., Chakrabati, A., Chiang, C. -F., Vanderwilt, S., Black, J., Chong, F., Martonosi, M., Suchara, M., Brown, K., Pedram, M., & Brun, T. (2012). Scaffold: Quantum Programming Language. Technical report, Princeton Univ NJ Dept of Computer Science.
Ahmad, A., Desouza, K. C., Maynard, S. B., Naseer, H., & Baskerville, R. L. (2020). How integration of cyber security management and incident response enables organizational learning. Journal of the Association for Information Science and Technology, 71(8), 939–953. https://doi.org/10.1002/asi.24311
Ahmad, A., Hadgkiss, J., & Ruighaver, A. B. (2012). Incident response teams - Challenges in supporting the organisational security function. Computers and Security, 31(5), 643–652. https://doi.org/10.1016/j.cose.2012.04.001
Ahmad, A., Maynard, S. B., Desouza, K. C., Kotsias, J., Whitty, M. T., & Baskerville, R. L. (2021). How can organizations develop situation awareness for incident response: A case study of management practice. Computers & Security, 101,. https://doi.org/10.1016/j.cose.2020.102122
Ahmad, A., Maynard, S. B., & Shanks, G. (2015). A case analysis of information systems and security incident responses. International Journal of Information Management, 35(6), 717–723. https://doi.org/10.1016/j.ijinfomgt.2015.08.001
Ahmad, A., Webb, J., Desouza, K. C., & Boorman, J. (2019). Strategically-motivated advanced persistent threat: Definition, process, tactics and a disinformation model of counterattack. Computers & Security, 86, 402–418. https://doi.org/10.1016/j.cose.2019.07.001
Ahmed, B. S., & Nibouche, F. (2018). Using survey to estimate the effort of setting up an Information Security Management System: Case ITC Organizations. In: 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), pp. 803–808. https://doi.org/10.1109/CoDIT.2018.8394907. IEEE, Thessaloniki, Greece.
Akinwumi, D. A., Iwasokun, G. B., Alese, B. K., & Oluwadare, S. A. (2018). A review of game theory approach to cyber security risk management. Nigerian Journal of Technology, 36(4), 1271. https://doi.org/10.4314/njt.v36i4.38
Aleksandrowicz, G., Alexander, T., Barkoutsos, P., Bello, L., Ben-Haim, Y., Bucher, D., Cabrera-Hernández, F. J., Carballo-Franquis, J., Chen, A., Chen, C. -F., & Others. (2019). Qiskit: An open-source framework for quantum computing. https://doi.org/10.5281/zenodo.2562111. Accessed 16 Mar 2019.
Alhawari, S., Karadsheh, L., Nehari Talet, A., & Mansour, E. (2012). Knowledge-Based Risk Management framework for Information Technology project. International Journal of Information Management, 32(1), 50–65. https://doi.org/10.1016/j.ijinfomgt.2011.07.002
Alshawabkeh, M., Li, X., & Sullabi, M. (2019). New Information Security Risk Management Framework as an Integral Part of Project Life Cycle. In: Proceedings of the 2019 5th International Conference on Humanities and Social Science Research (ICHSSR 2019). https://doi.org/10.2991/ichssr-19.2019.24. Atlantis Press, Paris, France.
Altenkirch, T., & Grattage, J. (2005). A Functional Quantum Programming Language. In: 20th Annual IEEE Symposium on Logic in Computer Science (LICS’ 05), pp. 249–258. IEEE, Chicago, IL, USA. https://doi.org/10.1109/LICS.2005.1
AndreSaraiva, D. (2022). How Should Quantum Computations Be Priced? Quantum Computing Report, GQI. https://quantumcomputingreport.com/how-should-quantum-computations-be-priced/
Aoyama, T., Sato, A., Lisi, G., & Watanabe, K. (2020). On the importance of agility, transparency, and positive reinforcement in cyber incident crisis communication. In S. Nadjm-Tehrani (Ed.), Critical Information Infrastructures Security (pp. 163–168). Cham: Springer.
Asfaw, A., Corcoles, A., Bello, L., Ben-Haim, Y., Bozzo-Rey, M., Bravyi, S., Bronn, N., Capelluto, L., Vazquez, A.C., Ceroni, J., Chen, R., Frisch, A., Gambetta, J., Garion, S., Gil, L., Gonzalez, S. D. L. P., Harkins, F., Imamichi, T., Kang, H., h. Karamlou, A., Loredo, R., McKay, D., Mezzacapo, A., Minev, Z., Movassagh, R., Nannicini, G., Nation, P., Phan, A., Pistoia, M., Rattew, A., Schaefer, J., Shabani, J., Smolin, J., Stenger, J., Temme, K., Tod, M., Wood, S., & Wootton., J. (2020). Learn Quantum Computation Using Qiskit. http://community.qiskit.org/textbook
Bhardwaj, A., & Sapra, V. (2021). Security Incidents & Response Against Cyber Attacks. Springer. https://doi.org/10.1007/978-3-030-69174-5
Bongiovanni, I. (2019). The least secure places in the universe? A systematic literature review on information security management in higher education. Computers & Security, 86, 350–357. https://doi.org/10.1016/j.cose.2019.07.003
Černý, V. (1993). Quantum computers and intractable (np-complete) computing problems. Physical Review A, 48, 116–119. https://doi.org/10.1103/PhysRevA.48.116
Clairambault, P., DeVisme, M., & Winskel, G. (2019). Game semantics for quantum programming. Proceedings of the ACM on Programming Languages, 3(POPL), 1–29.
Cutress, I. (2021). Intel Core I7-10700 Vs Core i7-10700K Review: Is 65W Comet Lake an Option? Anand’s Hardware Tech Page, Anandtech. https://www.anandtech.com/show/16343/intel-core-i710700-vs-core-i710700k-review-is-65w-comet-lake-an-option/2
Das, A., & Chakrabarti, B. K. (2008). Colloquium: Quantum annealing and analog quantum computation. Reviews of Modern Physics, 80(3), 1061.
Dashti, S., Giorgini, P., & Paja, E. (2017). Information Security Risk Management. In: Lecture Notes in Business Information Processing. FThe Practice of Enterprise Modeling, 305, 18–33. https://doi.org/10.1007/978-3-319-70241-4_2. Springer, Cham.
Debnath, B., Alghazo, J. M., Latif, G., Roychoudhuri, R., & Ghosh, S. K. (2020). An Analysis of Data Security and Potential Threat from IT Assets for Middle Card Players, Institutions and Individuals. In: Sustainable Waste Management: Policies and Case Studies. Sustainable Waste Management: Policies and Case Studies, pp. 403–419. https://doi.org/10.1007/978-981-13-7071-7_36. Springer, Singapore.
Dieterich, J. M., & Hartke, B. (2012). Empirical review of standard benchmark functions using evolutionary global optimization. arXiv preprint. arXiv:1207.4318
Dion, M. (2020). Cybersecurity policy and theory. In: Theoretical Foundations of Homeland Security, pp. 257–284. Routledge, London.
Eslamkhah, M., & Hosseini Seno, S. A. (2019). Identifying and Ranking Knowledge Management Tools and Techniques Affecting Organizational Information Security Improvement. Knowledge Management Research & Practice, 17(3), 276–305. https://doi.org/10.1080/14778238.2019.1599495
EuroStat: Electricity Price Statistics. (2022). Statistics Explained, European Commission. https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_price_statistics
Farhi, E., Goldstone, J., Gutmann, S., Lapan, J., Lundgren, A., & Preda, D. (2001). A quantum adiabatic evolution algorithm applied to random instances of an np-complete problem. Science, 292(5516), 472–475.
Farhi, E., Goldstone, J., & Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv preprint. arXiv:1411.4028
Glantz, C., Lenaeus, J., Landine, G., O’Neil, L.R., Leitch, R., Johnson, C., Lewis, J., & Rodger, R. (2017). Chapter 9. In: Martellini, M., Malizia, A. (eds.) Implementing an Information Security Program. Terrorism, Security, and Computation, pp. 179–197. https://doi.org/10.1007/978-3-319-62108-1_9. Springer, Cham.
Green, A. S., Lumsdaine, P. L., Ross, N. J., Selinger, P., & Valiron, B. (2013). Quipper. In: ACM SIGPLAN Notices, 48, 333–342. https://doi.org/10.1145/2499370.2462177. Association for Computing Machinery, New York, NY, USA.
Grispos, G., Glisson, W. B., & Storer, T. (2017). Enhancing security incident response follow-up efforts with lightweight agile retrospectives. Digital Investigation, 22, 62–73. https://doi.org/10.1016/j.diin.2017.07.006
Gritzalis, D., Iseppi, G., Mylonas, A., & Stavrou, V. (2018). Exiting the Risk Assessment Maze. ACM Computing Surveys, 51(1), 1–30. https://doi.org/10.1145/3145905
Grover, L. K. (1997). Quantum Mechanics Helps in Searching for a Needle in a Haystack. Physical Review Letters, 79(2), 325–328. https://doi.org/10.1103/PhysRevLett.79.325
Gyongyosi, L., & Imre, S. (2019). A Survey on quantum computing technology. Computer Science Review, 31, 51–71. https://doi.org/10.1016/j.cosrev.2018.11.002
Hariyanti, E., Djunaidy, A., & Siahaan, D. O. (2018). A Conceptual Model for Information Security Risk Considering Business Process Perspective. In: 2018 4th International Conference on Science and Technology (ICST), pp. 1–6. https://doi.org/10.1109/ICSTC.2018.8528678. IEEE, Yogyakarta, Indonesia.
He, Y., Zamani, E. D., Lloyd, S., & Luo, C. (2022). Agile incident response (air): Improving the incident response process in healthcare. International Journal of Information Management, 62,. https://doi.org/10.1016/j.ijinfomgt.2021.102435
Heim, B., Soeken, M., Marshall, S., Granade, C., Roetteler, M., Geller, A., Troyer, M., & Svore, K. (2020). Quantum programming languages. Nature Reviews. Physics, 2(12), 709–722. https://doi.org/10.1038/s42254-020-00245-7
Hidary, J. D. (2019). Quantum Computing: An Applied Approach. Cham: Springer.
IBM: The Quantum Decade. (2021). A Playbook for Achieving Awareness, Readiness, and Advantage. https://www.ibm.com/downloads/cas/J25G35OK
Johnston, E. R., Harrigan, N., & Gimeno-Segovia, M. (2019). Programming Quantum Computers: Essential Algorithms and Code Samples. Gravenstein Highway North, USA: O’Reilly Media.
Kirkpatrick, S., Gelatt, C. D., Jr, & Vecchi, M. P. (1983). Optimization by simulated annealing. science, 220(4598), 671–680.
Knight, R., & Nurse, J. R. C. (2020). A framework for effective corporate communication after cyber security incidents. Computers & Security, 99,. https://doi.org/10.1016/j.cose.2020.102036
Knill, E. (1996). Conventions for quantum pseudocode. Technical Report LAUR-96-2724, Los Alamos National Lab, NM (United States)
Liu, S., Wang, X., Zhou, L., Guan, J., Li, Y., He, Y., Duan, R., & Ying, M. (2018). Qsi\(>\): A quantum programming environment. In: Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 11180(LNCS), 133–164. https://doi.org/10.1007/978-3-030-01461-2_8. Springer.
Lucas, A. (2014). Ising formulations of many np problems. Frontiers in physics, 2, 5. https://doi.org/10.3389/fphy.2014.00005
Mahima, D. (2021). Cyber threat in public sector: Modeling an incident response framework. In: 2021 International Conference on Innovative Practices in Technology and Management (ICIPTM), pp. 55–60. https://doi.org/10.1109/ICIPTM52218.2021.9388333
Mailloux, L. O., Lewis, C. D., II, Riggs, C., & Grimaila, M. R. (2016). Post-quantum cryptography: what advancements in quantum computing mean for it professionals. IT Professional, 18(5), 42–47.
Maymin, P. (1996). Extending the Lambda Calculus to Express Randomized and Quantumized Algorithms. arXiv preprint quant-ph/9612052. arXiv:9612052. [quant-ph].
Mortazavi, S. A. R., & Safi-Esfahani, F. (2019). A checklist based evaluation framework to measure risk of information security management systems. International Journal of Information Technology (Singapore), 11(3), 517–534. https://doi.org/10.1007/s41870-019-00302-0
Mueck, L. (2017). Quantum software. Nature, 549(7671), 171–171.
Naseer, A., Naseer, H., Ahmad, A., Maynard, S. B., & Masood Siddiqui, A. (2021). Real-time analytics, incident response process agility and enterprise cybersecurity performance: A contingent resource-based analysis. International Journal of Information Management, 59,. https://doi.org/10.1016/j.ijinfomgt.2021.102334
Paltrinieri, N., & Reniers, G. (2017). Dynamic risk analysis for Seveso sites. Journal of Loss Prevention in the Process Industries, 49, 111–119. https://doi.org/10.1016/j.jlp.2017.03.023
Pakin, S. (2016). A quantum macro assembler. In: 2016 IEEE High Performance Extreme Computing Conference (HPEC), pp. 1–8. https://doi.org/10.1109/HPEC.2016.7761637
Piattini, M., Serrano, M., Perez-Castillo, R., Petersen, G., & Hevia, J. L. (2021). Toward a Quantum Software Engineering. IT Professional, 23(1), 62–66. https://doi.org/10.1109/MITP.2020.3019522
Pleta, T., Tvaronavičiene, M., & Della Casa, S. (2020). Cyber effect and security management aspects in critical energy infrastructures. Insights into Regional Development, 2(2), 538–548. https://doi.org/10.9770/IRD.2020.2.2(3)
Prasad, R., & Rohokale, V. (2020). Secure Incident Handling, pp. 203–216. Springer, Cham. https://doi.org/10.1007/978-3-030-31703-4_14
Proença, D., & Borbinha, J. (2018). Information Security Management Systems - A Maturity Model Based on ISO/IEC 27001. In: Lecture Notes in Business Information Processing. Business Information Systems, 320, 102–114. https://doi.org/10.1007/978-3-319-93931-5_8. Springer, Cham.
Rocke, D. (2000). Genetic algorithms+ data structures= evolution programs (3rd. Journal of the American Statistical Association, 95(449), 347.
Rosado, D. G., Moreno, J., Sánchez, L. E., Santos-Olmo, A., Serrano, M. A., & Fernández-Medina, E. (2021). Marisma-bida pattern: Integrated risk analysis for big data. Computers & Security, 102,. https://doi.org/10.1016/j.cose.2020.102155
Ross, R., Pillitteri, V., Graubart, R., Bodeau, D., & McQuaid, R. (2019). Developing cyber resilient systems: a systems security engineering approach. National Institute of Standards and Technology: Technical report.
Ruan, K. (2017). Introducing cybernomics: A unifying economic framework for measuring cyber risk. Computers & Security, 65, 77–89. https://doi.org/10.1016/j.cose.2016.10.009
Salvi, A., Spagnoletti, P., & Noori, N. S. (2022). Cyber-resilience of critical cyber infrastructures: Integrating digital twins in the electric power ecosystem. Computers & Security, 112,. https://doi.org/10.1016/j.cose.2021.102507
Sánchez, P., & Alonso, D. (2021). On the Definition of Quantum Programming Modules. Applied Sciences, 11(13), 5843.
Sardjono, W., & Cholik, M. I. (2018). Information Systems Risk Analysis Using Octave Allegro Method Based at Deutsche Bank. In: 2018 International Conference on Information Management and Technology (ICIMTech), pp. 38–42. https://doi.org/10.1109/ICIMTech.2018.8528108. IEEE, Jakarta, Indonesia.
Shor, P. W. (2002). Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th Annual Symposium on Foundations of Computer Science, pp. 124–134. IEEE Comput. Soc. Press, Santa Fe, NM, USA. https://doi.org/10.1109/SFCS.1994.365700. IEEE.
Smith, R. S., Curtis, M. J., & Zeng, W. J. (2016). A Practical Quantum Instruction Set Architecture. arXiv preprint. arXiv:1608.03355, arXiv:1608.03355
Srinivas, J., Das, A. K., & Kumar, N. (2019). Government regulations in cyber security: Framework, standards and recommendations. Future Generation Computer Systems, 92, 178–188. https://doi.org/10.1016/j.future.2018.09.063
Steiger, D. S., Häner, T., & Troyer, M. (2018). ProjectQ: an open source software framework for quantum computing. Quantum, 2, 49. arXiv:1612.08091, https://doi.org/10.22331/q-2018-01-31-49
Sun, H., & Xie, X. (2019). Threat evaluation method of warships formation air defense based on AR(p)-DITOPSIS. Journal of Systems Engineering and Electronics, 30(2), 297. https://doi.org/10.21629/JSEE.2019.02.09
Sutor, R. (2019). Dancing with Qubits. Birmingham, UK: Packt Publishing.
Svore, K., Roetteler, M., Geller, A., Troyer, M., Azariah, J., Granade, C., Heim, B., Kliuchnikov, V., Mykhailova, M., & Paz, A. (2018). Q#. In: Proceedings of the Real World Domain Specific Languages Workshop 2018. RWDSL2018, pp. 1–10. https://doi.org/10.1145/3183895.3183901. ACM Press, New York, New York, USA.
Szwaczyk, S., Wrona, K., & Amanowicz, M. (2018). Applicability of risk analysis methods to risk-aware routing in software-defined networks. In: 2018 International Conference on Military Communications and Information Systems (ICMCIS), pp. 1–7. https://doi.org/10.1109/ICMCIS.2018.8398688. IEEE, Warsaw, Poland.
Szabó, Z. (2017). The Information Security and IT Security Questions of Pension Payment. In: Key Engineering Materials, 755, 322–327. https://doi.org/10.4028/www.scientific.net/KEM.755.322. Trans Tech Publ, Cham.
Tam, T., Rao, A., & Hall, J. (2021). The good, the bad and the missing: A narrative review of cyber-security implications for australian small businesses. Computers & Security, 109,. https://doi.org/10.1016/j.cose.2021.102385
Tanczer, L. M., Brass, I., & Carr, M. (2018). Csirts and global cybersecurity: How technical experts support science diplomacy. Global Policy, 9(S3), 60–66. https://doi.org/10.1111/1758-5899.12625
Thakur, K., Qiu, M., Gai, K., & Ali, M. L. (2015). An Investigation on Cyber Security Threats and Security Models. In: 2015 IEEE 2nd International Conference on Cyber Security and Cloud Computing, pp. 307–311. https://doi.org/10.1109/CSCloud.2015.71. IEEE, New York, NY, USA.
Tiganoaia, B., Niculescu, A., Negoita, O., & Popescu, M. (2019). A New Sustainable Model for Risk Management-RiMM. Sustainability, 11(4), 1178. https://doi.org/10.3390/su11041178
Turskis, Z., Goranin, N., Nurusheva, A., & Boranbayev, S. (2019). Information Security Risk Assessment in Critical Infrastructure: A Hybrid MCDM Approach. Informatica, 30(1), 187–211. https://doi.org/10.15388/Informatica.2019.203
van der Kleij, R., Schraagen, J. M., Cadet, B., & Young, H. (2021). Developing decision support for cybersecurity threat and incident managers. Computers & Security, 102535. https://doi.org/10.1016/j.cose.2021.102535.
Wang, T., Gao, S., Li, X., & Ning, X. (2018). A meta-network-based risk evaluation and control method for industrialized building construction projects. Journal of Cleaner Production, 205, 552–564. https://doi.org/10.1016/j.jclepro.2018.09.127
Wecker, D., & Svore, K. M. (2014). LIQUi>: A Software Design Architecture and Domain-Specific Language for Quantum Computing. http://arxiv.org/abs/1402.4467
Wittek, P. (2014). Quantum Machine Learning: What Quantum Computing Means to Data Mining. Elsevier: Academic Press.
Wolf, M., & Serpanos, D. (2020). Chapter 3. Threats and Threat Analysis, pp. 35–45. https://doi.org/10.1007/978-3-030-25808-5_3. Springer, Cham.
Yoseviano, H. F., & Retnowardhani, A. (2018). The use of ISO/IEC 27001: 2009 to analyze the risk and security of information system assets: case study in xyz, ltd. In: 2018 International Conference on Information Management and Technology (ICIMTech), pp. 21–26. https://doi.org/10.1109/ICIMTech.2018.8528096. IEEE, Jakarta, Indonesia.
Zhao, J. (2020). Quantum Software Engineering: Landscapes and Horizons. http://arxiv.org/abs/2007.07047
Acknowledgements
We thank the support of the companies Sicaman Nuevas Tecnologías S.L. (https://www.sicaman.com) and Marisma Shield S.L. (https://www.emarisma.com) that have facilitated the validation of case studies and the use of the eMARISMA tool.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature. This work has been developed within the AETHER-UCLM (PID2020-112540RB-C42) funded by MCIN/AEI/10.13039/501100011033, ALBA-UCLM (TED2021-130355B-C31, id.4809130355-130355-28-521), ALBA-UC (TED2021-130355B-C33, id.3611130630-130630-28-521) funded by “Ministerio de Ciencia e Innovación”, and supported by the European Union’s Horizon 2020 Project “CyberSANE” under Grant Agreement No. 833683.
Author information
Authors and Affiliations
Contributions
Manuel A. Serrano led the manuscript writing and is responsible of the creation of the algorithm and validation of the proposal. Luis Enrique Sánchez and Antonio were in charge of the MARISMA framework. David García Rosado wrote Section 2. Eduardo Fernández-Medina, Vita Santa Barletta and Danilo Caivano contributed to Sections 1 and 5. All authors contributed to the writing and reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Serrano, M.A., Sánchez, L.E., Santos-Olmo, A. et al. Minimizing incident response time in real-world scenarios using quantum computing. Software Qual J 32, 163–192 (2024). https://doi.org/10.1007/s11219-023-09632-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11219-023-09632-6