iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s11128-024-04565-w
Enabling CV-MDI-QKD for weakly squeezed states using non-Gaussian operations | Quantum Information Processing Skip to main content
Springer Nature Link
Log in

Enabling CV-MDI-QKD for weakly squeezed states using non-Gaussian operations

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

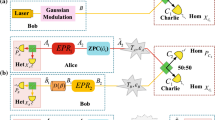
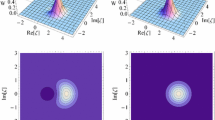
We propose a new non-Gaussian version of the continuous variables measurement device independent quantum key distribution (CV-MDI-QKD) protocol by utilizing a photon added-then-subtracted (PAS) state. We report that our single- and two-mode PAS-CV-MDI-QKD protocols outperform pure state CV-MDI-QKD protocol when considering weak squeezing and high noise, which is the practical regime. With such resources, CV-MDI-QKD is inaccessible when using a pure TMSV state, while PAS-CV-MDI-QKD can generate a useful key rate in this regime. We also compare PAS-CV-MDI-QKD with a two-mode photon replaced (2PR) state, which was not studied in low squeezing for MDI-QKD before.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

No datasets were generated or analysed during the current study.

References

  1. Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th Annual Symposium on Foundations of Computer Science, pp. 124–134. IEEE (1994)

  2. Scarani, V., Bechmann-Pasquinucci, H., Cerf, N.J., šek, M., Lütkenhaus, N., Peev, M.: The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301–1350 (2009). https://doi.org/10.1103/RevModPhys.81.1301

    Article  ADS  Google Scholar 

  3. Gisin, N., Ribordy, G., Tittel, W., Zbinden, H.: Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002). https://doi.org/10.1103/RevModPhys.74.145

    Article  ADS  Google Scholar 

  4. Bennett, C.H., Brassard, G.: Quantum cryptography: Public key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, India, p. 175 (1984)

  5. Nauerth, S., Moll, F., Rau, M., Fuchs, C., Horwath, J., Frick, S., Weinfurter, H.: Air-to-ground quantum communication. Nature Photon 7(5), 382–386 (2013)

    Article  ADS  Google Scholar 

  6. Grünenfelder, F., Boaron, A., Resta, G.V., Perrenoud, M., Rusca, D., Barreiro, C., Houlmann, R., Sax, R., Stasi, L., El-Khoury, S., Hänggi, E., Bosshard, N., Bussières, F., Zbinden, H.: Fast single-photon detectors and real-time key distillation enable high secret-key-rate quantum key distribution systems. Nature Photon. 17(5), 422–426 (2023). https://doi.org/10.1038/s41566-023-01168-2

    Article  ADS  Google Scholar 

  7. Ma, D., Liu, X., Huang, C., Chen, H., Lin, H., Wei, K.: Simple quantum key distribution using a stable transmitter-receiver scheme. Opt. Lett. 46(9), 2152 (2021). https://doi.org/10.1364/ol.418851

    Article  ADS  Google Scholar 

  8. Tian, X.-H., Yang, R., Zhang, J.-N., Yu, H., Zhang, Y., Fan, P., Chen, M., Gu, C., Ni, X., Hu, M., Cao, X., Hu, X., Zhao, G., Lu, Y.-Q., Yin, Z.-J., Liu, H.-Y., Gong, Y.-X., Xie, Z., Zhu, S.-N.: Drone-based quantum key distribution (2023). https://arxiv.org/abs/2302.14012

  9. Bouchard, F., Sit, A., Hufnagel, F., Abbas, A., Zhang, Y., Heshami, K., Fickler, R., Marquardt, C., Leuchs, G., Boyd, R., Karimi, E.: Quantum cryptography with twisted photons through an outdoor underwater channel. Opt. Express 26(17), 22563–22573 (2018). https://doi.org/10.1364/OE.26.022563

    Article  ADS  Google Scholar 

  10. Sax, R., Boaron, A., Boso, G., Atzeni, S., Crespi, A., Grünenfelder, F., Rusca, D., Al-Saadi, A., Bronzi, D., Kupijai, S., Rhee, H., Osellame, R., Zbinden, H.: High-speed integrated qkd system. Photon. Res. 11(6), 1007–1014 (2023). https://doi.org/10.1364/PRJ.481475

    Article  Google Scholar 

  11. Wei, K., Hu, X., Du, Y., Hua, X., Zhao, Z., Chen, Y., Huang, C., Xiao, X.: Resource-efficient quantum key distribution with integrated silicon photonics (2023). https://arxiv.org/abs/2212.12980

  12. Du, Y., Zhu, X., Hua, X., Zhao, Z., Hu, X., Qian, Y., Xiao, X., Wei, K.: Silicon-based decoder for polarization-encoding quantum key distribution (2022). https://arxiv.org/abs/2212.04019

  13. Wei, K., Li, W., Tan, H., Li, Y., Min, H., Zhang, W.-J., Li, H., You, L., Wang, Z., Jiang, X., Chen, T.-Y., Liao, S.-K., Peng, C.-Z., Xu, F., Pan, J.-W.: High-speed measurement-device-independent quantum key distribution with integrated silicon photonics. Phys. Rev. X (2020). https://doi.org/10.1103/physrevx.10.031030

    Article  Google Scholar 

  14. Ralph, T.C.: Security of continuous-variable quantum cryptography. Phys. Rev. A 62, 062306 (2000). https://doi.org/10.1103/PhysRevA.62.062306

    Article  ADS  Google Scholar 

  15. Grosshans, F., Grangier, P.: Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902 (2002). https://doi.org/10.1103/PhysRevLett.88.057902

    Article  ADS  Google Scholar 

  16. Weedbrook, C., Pirandola, S., García-Patrón, R., Cerf, N.J., Ralph, T.C., Shapiro, J.H., Lloyd, S.: Gaussian quantum information. Rev. Modern Phys. 84(2), 621 (2012)

    Article  ADS  Google Scholar 

  17. Laudenbach, F., Pacher, C., Fung, C.F., Poppe, A., Peev, M., Schrenk, B., Hentschel, M., Walther, P., Hübel, H.: Continuous-variable quantum key distribution with gaussian modulation-the theory of practical implementations. Adv. Quant. Technol. (2018). https://doi.org/10.1002/qute.201800011

    Article  Google Scholar 

  18. Grosshans, F.: Collective attacks and unconditional security in continuous variable quantum key distribution. Phys. Rev. Lett. 94(2), 020504 (2005)

    Article  ADS  Google Scholar 

  19. Renner, R., Cirac, J.I.: de finetti representation theorem for infinite-dimensional quantum systems and applications to quantum cryptography. Phys. Rev. Lett. 102, 110504 (2009). https://doi.org/10.1103/PhysRevLett.102.110504

    Article  ADS  Google Scholar 

  20. Leverrier, A.: Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. (2015). https://doi.org/10.1103/physrevlett.114.070501

    Article  Google Scholar 

  21. Zhang, Y., Chen, Z., Pirandola, S., Wang, X., Zhou, C., Chu, B., Zhao, Y., Xu, B., Yu, S., Guo, H.: Long-distance continuous-variable quantum key distribution over 202.81 km of fiber. Phys. Rev. Lett. (2020). https://doi.org/10.1103/physrevlett.125.010502

    Article  Google Scholar 

  22. Zhang, G., Haw, J.Y., Cai, H., Xu, F., Assad, S.M., Fitzsimons, J.F., Zhou, X., Zhang, Y., Yu, S., Wu, J., Ser, W., Kwek, L.C., Liu, A.Q.: An integrated silicon photonic chip platform for continuous-variable quantum key distribution. Nat. Photon. 13(12), 839–842 (2019). https://doi.org/10.1038/s41566-019-0504-5

    Article  ADS  Google Scholar 

  23. Xu, F., Wei, K., Sajeed, S., Kaiser, S., Sun, S., Tang, Z., Qian, L., Makarov, V., Lo, H.-K.: Experimental quantum key distribution with source flaws. Phys. Rev. A 92(3), 032305 (2015)

    Article  ADS  Google Scholar 

  24. Li, H.-W., Wang, S., Huang, J.-Z., Chen, W., Yin, Z.-Q., Li, F.-Y., Zhou, Z., Liu, D., Zhang, Y., Guo, G.-C., et al.: Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources. Phys. Rev. A 84(6), 062308 (2011)

    Article  ADS  Google Scholar 

  25. Zhao, Y., Fung, C.-H.F., Qi, B., Chen, C., Lo, H.-K.: Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A 78(4), 042333 (2008)

    Article  ADS  Google Scholar 

  26. Makarov, V., Anisimov, A., Skaar, J.: Effects of detector efficiency mismatch on security of quantum cryptosystems. Phys. Rev. A 74(2), 022313 (2006)

    Article  ADS  Google Scholar 

  27. Lamas-Linares, A., Kurtsiefer, C.: Breaking a quantum key distribution system through a timing side channel. Opt. Express 15(15), 9388–9393 (2007)

    Article  ADS  Google Scholar 

  28. Lo, H.-K., Curty, M., Qi, B.: Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108(13), 130503 (2012)

    Article  ADS  Google Scholar 

  29. Acín, A., Brunner, N., Gisin, N., Massar, S., Pironio, S., Scarani, V.: Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98(23), 230501 (2007)

    Article  ADS  Google Scholar 

  30. Yang, Y., Li, F.-L.: Entanglement properties of non-gaussian resources generated via photon subtraction and addition and continuous-variable quantum-teleportation improvement. Phys. Rev. A 80, 022315 (2009). https://doi.org/10.1103/PhysRevA.80.022315

    Article  ADS  Google Scholar 

  31. Lee, S.-Y., Ji, S.-W., Kim, H.-J., Nha, H.: Enhancing quantum entanglement for continuous variables by a coherent superposition of photon subtraction and addition. Phys. Rev. A 84, 012302 (2011). https://doi.org/10.1103/PhysRevA.84.012302

    Article  ADS  Google Scholar 

  32. Ourjoumtsev, A., Dantan, A., Tualle-Brouri, R., Grangier, P.: Increasing entanglement between gaussian states by coherent photon subtraction. Phys. Rev. Lett. 98, 030502 (2007). https://doi.org/10.1103/PhysRevLett.98.030502

    Article  ADS  Google Scholar 

  33. Takahashi, H., Neergaard-Nielsen, J.S., Takeuchi, M., Takeoka, M., Hayasaka, K., Furusawa, A., Sasaki, M.: Entanglement distillation from gaussian input states. Nat. Photon. 4(3), 178–181 (2010)

    Article  ADS  Google Scholar 

  34. Kurochkin, Y., Prasad, A.S., Lvovsky, A.I.: Distillation of the two-mode squeezed state. Phys. Rev. Lett. 112, 070402 (2014). https://doi.org/10.1103/PhysRevLett.112.070402

    Article  ADS  Google Scholar 

  35. Boyd, R.W., Chan, K.W.C., O’Sullivan, M.N.: Quantum weirdness in the lab. Science 317(5846), 1874–1875 (2007). https://doi.org/10.1126/science.1148947

    Article  Google Scholar 

  36. Bartley, T.J., Walmsley, I.A.: Directly comparing entanglement-enhancing non-gaussian operations. New J. Phys. 17(2), 023038 (2015)

    Article  ADS  Google Scholar 

  37. Borelli, L.F.M., Aguiar, L.S., Roversi, J.A., Vidiella-Barranco, A.: Quantum key distribution using continuous-variable non-gaussian states. Quantum Inf. Process. 15(2), 893–904 (2015). https://doi.org/10.1007/s11128-015-1193-8

    Article  ADS  MathSciNet  Google Scholar 

  38. Aguiar, L.S., Borelli, L.F.M., Roversi, J.A., Vidiella-Barranco, A.: Performance analysis of continuous-variable quantum key distribution using non-gaussian states. Quantum Inf. Process. (2022). https://doi.org/10.1007/s11128-022-03645-z

    Article  MathSciNet  Google Scholar 

  39. Hu, L., Al-amri, M., Liao, Z., Zubairy, M.S.: Continuous-variable quantum key distribution with non-gaussian operations. Phys. Rev. A 102, 012608 (2020). https://doi.org/10.1103/PhysRevA.102.012608

    Article  ADS  MathSciNet  Google Scholar 

  40. Ma, H.-X., Huang, P., Bai, D.-Y., Wang, S.-Y., Bao, W.-S., Zeng, G.-H.: Continuous-variable measurement-device-independent quantum key distribution with photon subtraction. Phys. Rev. A 97(4), 042329 (2018)

    Article  ADS  Google Scholar 

  41. Ye, W., Zhong, H., Wu, X., Hu, L., Guo, Y.: Continuous-variable measurement-device-independent quantum key distribution via quantum catalysis. Quantum Inf. Process. 19(10), 1–22 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  42. Khan, M.B., Waseem, M., Irfan, M., Mehmood, A., Qamar, S.: Zero-photon catalysis based eight-state discrete modulated measurement-device-independent continuous-variable quantum key distribution. J. Opt. Soc. Am. B 40(4), 763–772 (2023). https://doi.org/10.1364/JOSAB.482577

    Article  ADS  Google Scholar 

  43. Li, Z., Zhang, Y.-C., Xu, F., Peng, X., Guo, H.: Continuous-variable measurement-device-independent quantum key distribution. Phys. Rev. A 89(5), 052301 (2014)

    Article  ADS  Google Scholar 

  44. Vahlbruch, H., Mehmet, M., Danzmann, K., Schnabel, R.: Detection of 15 db squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency. Phys. Rev. Lett. 117, 110801 (2016). https://doi.org/10.1103/PhysRevLett.117.110801

    Article  ADS  Google Scholar 

  45. Ma, S.-L., Li, X.-K., Xie, J.-K., Li, F.-L.: Two-mode squeezed states of two separated nitrogen-vacancy-center ensembles coupled via dissipative photons of superconducting resonators. Phys. Rev. A 99, 012325 (2019). https://doi.org/10.1103/PhysRevA.99.012325

    Article  ADS  Google Scholar 

  46. Mølmer, K.: Non-gaussian states from continuous-wave gaussian light sources. Phys. Rev. A 73, 063804 (2006). https://doi.org/10.1103/PhysRevA.73.063804

    Article  ADS  Google Scholar 

  47. Singh, J., Bose, S.: Non-gaussian operations in measurement-device-independent quantum key distribution. Phys. Rev. A 104, 052605 (2021). https://doi.org/10.1103/PhysRevA.104.052605

    Article  ADS  Google Scholar 

  48. Mardani, Y., Shafiei, A., Ghadimi, M., Abdi, M.: Continuous-variable entanglement distillation by cascaded photon replacement. Phys. Rev. A (2020). https://doi.org/10.1103/physreva.102.012407

    Article  Google Scholar 

  49. Malpani, P., Thapliyal, K., Banerji, J., Pathak, A.: Enhancement of non-Gaussianity and nonclassicality of photon added displaced Fock state: A quantitative approach (2021). https://arxiv.org/abs/2109.12145

  50. Thapliyal, K., Samantray, N.L., Banerji, J., Pathak, A.: Comparison of lower- and higher-order nonclassicality in photon added and subtracted squeezed coherent states. Phys. Lett. A 381(37), 3178–3187 (2017). https://doi.org/10.1016/j.physleta.2017.08.019

    Article  Google Scholar 

  51. Zavatta, A., Viciani, S., Bellini, M.: Quantum-to-classical transition with single-photon-added coherent states of light. Science 306(5696), 660–662 (2004). https://doi.org/10.1126/science.1103190

    Article  ADS  Google Scholar 

  52. Hosseinidehaj, N., Malaney, R.: Cv-mdi quantum key distribution via satellite. Quantum Inf. Comput. (2017). https://doi.org/10.26421/qic17.5-6

  53. Hosseinidehaj, N.: Continuous-variable quantum communication over free-space lossy channels. PhD thesis, The University of New South Wales (2017)

  54. Villasenor, E., Malaney, R.: Improving qkd for entangled states with low squeezing via non-gaussian operations. In: 2019 IEEE Globecom Workshops (GC Wkshps), pp. 1–6 (2019). https://doi.org/10.1109/GCWkshps45667.2019.9024548

  55. Pirandola, S., Ottaviani, C., Spedalieri, G., Weedbrook, C., Braunstein, S., Lloyd, S., Gehring, T., Jacobsen, C., Andersen, U.: High-rate measurement-device-independent quantum cryptography. Nat. Photon. 9, 397–402 (2015). https://doi.org/10.1038/nphoton.2015.83

    Article  ADS  Google Scholar 

  56. Vidal, G., Werner, R.F.: Computable measure of entanglement. Phys. Rev. A 65, 032314 (2002). https://doi.org/10.1103/PhysRevA.65.032314

    Article  ADS  Google Scholar 

  57. Plenio, M.B.: Logarithmic negativity: a full entanglement monotone that is not convex. Phys. Rev. Lett. 95, 090503 (2005). https://doi.org/10.1103/PhysRevLett.95.090503

    Article  ADS  Google Scholar 

Download references

Author information

Author notes

  1. Jian Li and Aeysha Khalique have contributed equally to this work.

Authors and Affiliations

  1. Department of Physics, Syed Babar Ali School of Science and Engineering, Lahore University of Management Sciences, Lahore, 54792, Pakistan

    Farsad Ahmad & Aeysha Khalique

  2. School of Natural Sciences, National University of Sciences and Technology, Islamabad, 44000, Pakistan

    Farsad Ahmad & Aeysha Khalique

  3. Information Security Center, State Key Laboratory of Networking and Switching Technology Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Jian Li

  4. National Centre for Physics (NCP), Shahdra Valley Road, Islamabad, 44000, Pakistan

    Aeysha Khalique

Authors
  1. Farsad Ahmad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aeysha Khalique
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

FA did the main work and analysis. JL contributed in conceptualisation. AK supervised the work and contributed in analysis.

Corresponding author

Correspondence to Farsad Ahmad.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmad, F., Li, J. & Khalique, A. Enabling CV-MDI-QKD for weakly squeezed states using non-Gaussian operations. Quantum Inf Process 23, 353 (2024). https://doi.org/10.1007/s11128-024-04565-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-024-04565-w

Keywords

Search

Navigation