iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s11128-022-03787-0
Phase-matching quantum key distribution based on heralded pair-coherent source | Quantum Information Processing Skip to main content

Advertisement

Springer Nature Link
Log in

Phase-matching quantum key distribution based on heralded pair-coherent source

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

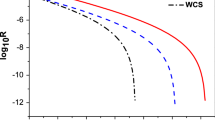
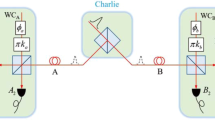
Twin-field quantum key distribution (TF-QKD) is known for its capacity of overcoming the fundamental rate-distance limit of QKD, and a variety of its variants have been derived. One of them, the phase-matching quantum key distribution (PM-QKD) not only inherits the high rate-distance capacity, but also outperforms the original TF-QKD. Moreover, the relatively less single-photon component of the most frequently used weak coherent source (WCS) makes it unable to meet the high-performance requirements of communication. In this paper, we propose a four-intensity decoy-state PM-QKD protocol based on heralded pair-coherent source to improve the secure key rate and the practicality. The simulations show that the secure key rate of our scheme is about an order of magnitude higher than that of four-intensity decoy-state PM-QKD protocol based on WCS. Meanwhile, the transmission distance is increased by more than 100 km. And the performance of our protocol has been greatly improved, in comparison with the better performance protocol known as ‘new PM-QKD’. In addition, the proposed protocol also shows excellent performance when finite data size and statistical fluctuation are considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

All data generated or analyzed during this study are included in this published article.

References

  1. Mayers, D.: Unconditional security in quantum cryptography. J. ACM 48(3), 351–406 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  2. Lo, H.K., Chau, H.F.: Unconditional security of quantum key distribution over arbitrarily long distances. Science 283(5410), 2050–2056 (1999)

    Article  ADS  Google Scholar 

  3. Shor, P.W., Preskill, J.: Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85(2), 441 (2000)

    Article  ADS  Google Scholar 

  4. Bennett, C. H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers Systems and Signal Processing, pp. 175-C179 (1984)

  5. Wang, X.B.: Decoy-state protocol for quantum cryptography with four different intensities of coherent light. Phys. Rev. A 72(1), 012322 (2005)

    Article  ADS  Google Scholar 

  6. Wang, X.B.: Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94(23), 230503 (2005)

    Article  ADS  Google Scholar 

  7. Lo, H.K., Ma, X., Chen, K.: Decoy state quantum key distribution. Phys. Rev. Lett. 94(23), 230504 (2005)

    Article  ADS  Google Scholar 

  8. Wang, X.B., Yang, L., Peng, C.Z., Pan, J.W.: Decoy-state quantum key distribution with both source errors and statistical fluctuations. New J. Phys. 11(7), 075006 (2009)

    Article  ADS  Google Scholar 

  9. Lo, H.K., Curty, M., Qi, B.: Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108(13), 130503 (2012)

    Article  ADS  Google Scholar 

  10. Ma, X., Razavi, M.: Alternative schemes for measurement-device-independent quantum key distribution. Phys. Rev. A 86(6), 062319 (2012)

    Article  ADS  Google Scholar 

  11. Wang, L., Zhao, S.M., Gong, L.Y., Cheng, W.W.: Free-space measurement-device-independent quantum-key-distribution protocol using decoy states with orbital angular momentum. Chin. Phys. B 24(12), 120307 (2015)

    Article  ADS  Google Scholar 

  12. Zhou, Y.H., Yu, Z.W., Wang, X.B.: Making the decoy-state measurement-device-independent quantum key distribution practically useful. Phys. Rev. A 93(4), 042324 (2016)

    Article  ADS  Google Scholar 

  13. Wu, X.D., Zhou, L., Zhong, W., Sheng, Y.B.: High-capacity measurement-device-independent quantum secure direct communication. Quantum Inf. Process. 19(10), 1–14 (2020)

    Article  ADS  MathSciNet  Google Scholar 

  14. Cui, Z.X., Zhong, W., Zhou, L., Sheng, Y.B.: Measurement-device-independent quantum key distribution with hyper-encoding. Sci. China Phys. Mech. Astron. 62(11), 1–10 (2019)

    Article  Google Scholar 

  15. Yan, Y.F., Zhou, L., Zhong, W., Sheng, Y.B.: Measurement-device-independent quantum key distribution of multiple degrees of freedom of a single photon. Front. Phys. 16(1), 1–11 (2021)

    Article  Google Scholar 

  16. Mizutani, A., Imoto, N., Tamaki, K.: Robustness of the round-robin differential-phase-shift quantum-key-distribution protocol against source flaws. Phys. Rev. A 92(6), 060303 (2015)

    Article  ADS  Google Scholar 

  17. Zhang, Y.Y., Bao, W.S., Zhou, C., Li, H.W., Wang, Y., Jiang, M.S.: Practical round-robin differential phase-shift quantum key distribution. Opt. Express 24(18), 20763–20773 (2016)

    Article  ADS  Google Scholar 

  18. Mao, Q.P., Wang, L., Zhao, S.M.: Decoy-state round-robin differential-phase-shift quantum key distribution with source errors. Quantum Inf. Process. 19(2), 1–12 (2020)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Pirandola, S., Laurenza, R., Ottaviani, C., Banchi, L.: Fundamental limits of repeaterless quantum communications. Nat. Commun. 8(1), 1–15 (2017)

    Article  Google Scholar 

  20. Lucamarini, M., Yuan, Z.L., Dynes, J.F., Shields, A.J.: Overcoming the rate-distance limit of quantum key distribution without quantum repeaters. Nature 557(7705), 400–403 (2018)

    Article  ADS  Google Scholar 

  21. Wang, X.B., Yu, Z.W., Hu, X.L.: Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 98(6), 062323 (2018)

    Article  ADS  Google Scholar 

  22. Ma, X., Zeng, P., Zhou, H.: Phase-matching quantum key distribution. Phys. Rev. X 8(3), 031043 (2018)

    Google Scholar 

  23. Cui, C., Yin, Z.Q., Wang, R., Chen, W., Wang, S., Guo, G.C., Han, Z.F.: Twin-field quantum key distribution without phase postselection. Phys. Rev. Appl. 11(3), 034053 (2019)

    Article  ADS  Google Scholar 

  24. Xue, K., Zhao, S., Mao, Q., Xu, R.: Plug-and-play sending-or-not-sending twin-field quantum key distribution. Quantum Inf. Process. 20(10), 1–16 (2021)

    Article  ADS  MathSciNet  Google Scholar 

  25. Li, W.T., Wang, L., Li, W., Zhao, S.M.: Phase-matching quantum key distribution with light source monitoring. Chin. Phys. B 31(5), 050310 (2022)

    Article  ADS  Google Scholar 

  26. Li, W., Wang, L., Zhao, S.: Phase matching quantum key distribution based on single-photon entanglement. Sci. Rep. 9(1), 1–12 (2019)

    ADS  Google Scholar 

  27. Zeng, P., Wu, W., Ma, X.: Symmetry-protected privacy: beating the rate-distance linear bound over a noisy channel. Phys. Rev. Appl. 13(6), 064013 (2020)

    Article  ADS  Google Scholar 

  28. Chen, G., Wang, L., Li, W., Zhao, Y., Zhao, S.M., Gruska, J.: Multiple-pulse phase-matching quantum key distribution. Quantum Inf. Process. 19(11), 1–16 (2020)

    Article  MathSciNet  Google Scholar 

  29. Yu, Y., Wang, L., Zhao, S., Mao, Q.: Decoy-state phase-matching quantum key distribution with source errors. Opt. Express 29(2), 2227–2243 (2021)

    Article  ADS  Google Scholar 

  30. Zhang, X.X., Wang, Y., Jiang, M.S., Zhou, C., Lu, Y.F., Bao, W.S.: Finite-key analysis of asymmetric phase-matching quantum key distribution with unstable sources. J. Opt. Soc. Am. B 38(3), 724–731 (2021)

    Article  ADS  Google Scholar 

  31. Yu, Y., Wang, L., Zhao, S., Mao, Q.: Prefixed-threshold real-time selection for free-space phase-matching quantum key distribution. Europhys. Lett. 138(2), 28001 (2022)

    Article  ADS  Google Scholar 

  32. Agarwal, G.S.: Generation of pair coherent states and squeezing via the competition of four-wave mixing and amplified spontaneous emission. Phys. Rev. Lett. 57(7), 827 (1986)

    Article  ADS  Google Scholar 

  33. Zhang, S., Zou, X., Li, C., Jin, C., Guo, G.: A universal coherent source for quantum key distribution. Chin. Sci. Bull. 54(11), 1863–1871 (2009)

    MATH  Google Scholar 

  34. Wang, L., Zhao, S.: Round-robin differential-phase-shift quantum key distribution with heralded pair-coherent sources. Quantum Inf. Process. 16(4), 100 (2017)

    Article  ADS  MATH  Google Scholar 

  35. Chen, D., Shang-Hong, Z., Lei, S.: Measurement device-independent quantum key distribution with heralded pair coherent state. Quantum Inf. Process. 15(10), 4253–4263 (2016)

    Article  ADS  MATH  Google Scholar 

  36. Wang, X., Wang, Y., Chen, R.K., Zhou, C., Li, H.W., Bao, W.S.: Measurement-device-independent quantum key distribution with heralded pair coherent state. Laser Phys. 26(6), 065203 (2016)

    Article  ADS  Google Scholar 

  37. Xu, R., Zhao, S.: Sending or not sending quantum key distribution based on heralded pair-coherent source. Laser Optoelectron. Progress 58(23), 2327001 (2021)

    Google Scholar 

  38. Bennett, C.H., DiVincenzo, D.P., Smolin, J.A., Wootters, W.K.: Mixed-state entanglement and quantum error correction. Phys. Rev. A 54(5), 3824 (1996)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Horikiri, T., Kobayashi, T.: Decoy state quantum key distribution with a photon number resolved heralded single photon source. Phys. Rev. A 73(3), 032331 (2006)

    Article  ADS  Google Scholar 

  40. Wang, Y., Bao, W.S., Zhou, C., Jiang, M.S., Li, H.W.: Tight finite-key analysis of a practical decoy-state quantum key distribution with unstable sources. Phys. Rev. A 94(3), 032335 (2016)

    Article  ADS  Google Scholar 

  41. Ma, X., Qi, B., Zhao, Y., Lo, H.K.: Practical decoy state for quantum key distribution. Phys. Rev. A 72(1), 012326 (2005)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (NSFC) (61871234). Yang Yu acknowledges the Postgraduate Research & Practice Innovation Program of Jiangsu Province (Grant KYCX22_0958).

Author information

Authors and Affiliations

  1. Institute of Signal Processing Transmission, Nanjing University of Posts and Telecommunications (NUPT), Nanjing, 210003, China

    Le Han, Yang Yu, Wenhao Lu, Ke Xue, Wenting Li & Shengmei Zhao

  2. Key Lab of Broadband Wireless Communication and Sensor Network Technology, Ministry of Education, Nanjing, 210003, China

    Shengmei Zhao

Authors
  1. Le Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yang Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wenhao Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ke Xue
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wenting Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Shengmei Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shengmei Zhao.

Ethics declarations

Conflict of interest

The authors have no conflicts to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, L., Yu, Y., Lu, W. et al. Phase-matching quantum key distribution based on heralded pair-coherent source. Quantum Inf Process 22, 37 (2023). https://doi.org/10.1007/s11128-022-03787-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-022-03787-0

Keywords

Search

Navigation