Multi-view Subspace Clustering Based on Unified Measure Standard

Abstract

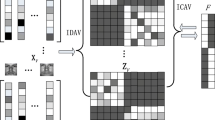
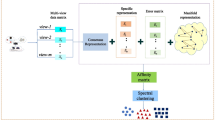
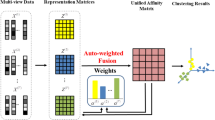
In recent years, multi-view subspace clustering has attracted extensive attention. In order to improve the clustering performance, the previous work tries to explore the consistency and specificity between different views by making the common representation matrix as close to the representation matrix learned in each view as possible. However, the values of the elements corresponding to a similar degree of the strong or weak relationship often have different magnitude levels in the representation matrix learned in each view. In this situation, the above strategy will make the information of some views ignored or magnified. To overcome this limitation, we propose a novel multi-view subspace clustering method in this paper. Because our proposed method can normalize the degree of the strong or weak relationship in each view to the unified measure standard by scaling the representation matrix learned in each view, the consistency and specificity between different views will be mined more effectively. In addition, we provide a theoretical analysis of the convergence and computation complexity of our numerical algorithm. The experimental results on several benchmark data sets indicate that our proposed method is not only effective but also efficient for the problem of multi-view subspace clustering.

Appendix A: Proof of Theorem 1

Suppose we have obtained $Z^{(v)}_{k}, \mu _{k}$ and $C_{k}$ by our algorithm. In the next round of iteration, when updating $Z^{(v)}$, $\mu _{k}$ and $C_{k}$ are fixed. Since Eq. (6) is a closed-form solution, $Z^{(v)}_{k+1}$ is the optimal solution. Therefore, it will minimize the value of the objective function with $\mu _{k}$ and $C_{k}$ fixed, i.e.

$$\begin{aligned} f(Z^{(v)}_{k+1},\mu _{k},C_{k})\le f(Z^{(v)}_{k},\mu _{k},C_{k}). \end{aligned}$$

(A1)

When updating $\mu , Z^{(v)}_{k+1}$ and $C_{k}$ are fixed. Since both Eqs. (8) and (10) are the closed-form solution, $\mu _{k+1}$ is the optimal solution. Therefore, it will minimize the value of the objective function with $Z^{(v)}_{k+1}$ and $C_{k}$ fixed, i.e.

$$\begin{aligned} f(Z^{(v)}_{k+1},\mu _{k+1},C_{k})\le f(Z^{(v)}_{k+1},\mu _{k},C_{k}). \end{aligned}$$

(A2)

When updating $C, Z^{(v)}_{k+1}$ and $\mu _{k+1}$ are fixed. Since Eq. (12) is also a closed-form solution, $C_{k+1}$ is the optimal solution. Therefore, it will minimize the value of the objective function with $Z^{(v)}_{k+1}$ and $\mu _{k+1}$ fixed, i.e.

$$\begin{aligned} f(Z^{(v)}_{k+1},\mu _{k+1},C_{k+1})\le f(Z^{(v)}_{k+1},\mu _{k+1},C_{k}). \end{aligned}$$

(A3)

Hence, after a round of iteration, the objective function value will decrease, i.e.

$$\begin{aligned} f(Z^{(v)}_{k+1},\mu _{k+},C_{k+1})\le f(Z^{(v)}_{k},\mu _{k},C_{k}). \end{aligned}$$

(A4)

Hence, Theorem 1 is proved.