iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s11063-015-9482-x
Dissipativity and Passivity Analysis of Markovian Jump Neural Networks with Two Additive Time-Varying Delays | Neural Processing Letters Skip to main content
Springer Nature Link
Log in

Dissipativity and Passivity Analysis of Markovian Jump Neural Networks with Two Additive Time-Varying Delays

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

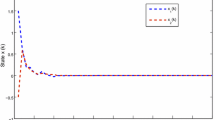
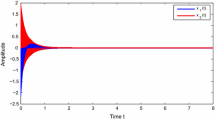
In this paper, we investigated a problem of dissipativity and passivity analysis of Markovian jump neural networks involving two additive time-varying delays. By considering proper triple integral terms in the Lyapunov–Krasovskii functional, several sufficient conditions are derived for verifying the dissipativity criteria of neural networks. The relationship between the time-varying delay and its lower and upper bounds is taken into account when estimating the upper bound of the time delay. As a result, some improved delay dissipativity criteria for neural networks with two additive time-varying delays components are proposed. The dissipativity criteria that depend on the upper bounds of the leakage time-varying delay and its derivative is given in terms of linear matrix inequalities, which can be efficiently solved via standard numerical software. Finally, three numerical examples are given to show the effectiveness of the proposed results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Gupta MM, Jin L, Homma N (2003) Static and dynamic neural networks. Wiley, New York

    Book  Google Scholar 

  2. Sakthivel R, Vadivel P, Mathiyalagan K, Arunkumar A, Sivachitra M (2015) Design of state estimator for bidirectional associative memory neural networks with leakage delays. Inf Sci 296:263–274

    Article  MathSciNet  Google Scholar 

  3. Zhu Q, Cao J, Hayat T, Alsaadi F (2015) Robust stability of Markovian jump stochastic neural networks with time delays in the leakage terms. Neural Process Lett 41:1–27

    Article  Google Scholar 

  4. Arunkumar A, Sakthivel R, Mathiyalagan K (2015) Robust reliable \(H_{\infty }\) control for stochastic neural networks with randomly occurring delays. Neurocomputing 149:1524–1534

    Article  Google Scholar 

  5. Kwon OM, Park MJ, Park JH, Lee SM, Cha EJ (2014) Improved results on stability of linear systems with time-varying delays via Wirtinger-based integral inequality. J Frankl Inst 351:5386–5398

    Article  MathSciNet  Google Scholar 

  6. Wang X, Yu J, Li C, Wang H, Huang T, Huang J (2015) Robust stability of stochastic fuzzy delayed neural networks with impulsive time window. Neural Netw 67:84–91

    Article  Google Scholar 

  7. Jiang P, Zeng Z, Chen J (2015) Almost periodic solutions for a memristor-based neural networks with leakage, time-varying and distributed delays. Neural Netw 68:34–45

    Article  Google Scholar 

  8. Zhu Q, Rakkiyappan R, Chandrasekar A (2014) Stochastic stability of Markovian jump BAM neural networks with leakage delays and impulse control. Neurocomputing 136:136–151

    Article  Google Scholar 

  9. Samli R (2015) A new delay-independent condition for global robust stability of neural networks with time delays. Neural Netw 66:131–137

    Article  Google Scholar 

  10. Zhang H, Yang F, Liu X, Zhang Q (2013) Stability analysis for neural networks with time-varying delay based on quadratic convex combination. IEEE Trans Neural Netw Learn Syst 24:513–521

    Article  Google Scholar 

  11. Guo Z, Wang J, Yan Z (2014) Attractivity analysis of memristor-based cellular neural networks with time-varying delays. IEEE Trans Neural Netw Learn Syst 25:704–717

    Article  Google Scholar 

  12. Verriest E (2011) Inconsistencies in systems with time-varying delays and their resolution. IMA J Math Control Inf 28:147–162

    Article  MathSciNet  MATH  Google Scholar 

  13. He Y, Liu GP, Rees D (2007) New delay-dependent stability criteria for neural networks with time-varying delay. IEEE Trans Neural Netw 18:310–314

    Article  Google Scholar 

  14. Zhao Y, Gao H, Mou S (2008) Asymptotic stability analysis of neural networks with successive time delay components. Neurocomputing 71:2848–2856

    Article  Google Scholar 

  15. Shao H, Han Q (2011) New delay-dependent stability criteria for neural networks with two additive time-varying delay components. IEEE Trans Neural Netw 22:812–818

    Article  Google Scholar 

  16. Tian J, Zhong S (2012) Improved delay-dependent stability criteria for neural networks with two additive time-varying delay components. Neurocomputing 77:114–119

    Article  Google Scholar 

  17. Chen H (2013) Improved stability criteria for neural networks with two additive time-varying delay components. Circuits Syst Signal Process 32:1977–1990

    Article  MathSciNet  Google Scholar 

  18. Zheng CD, Zhang X, Wang Z (2015) Mode and delay-dependent stochastic stability conditions of fuzzy neural networks with Markovian jump parameters. Neural Process Lett. doi:10.1007/s11063-015-9413-x

  19. Chen H, Wang J, Wang L (2014) New criteria on delay-dependent robust stability for uncertain Markovian stochastic delayed neural networks, Neural Process Lett. doi:10.1007/s11063-014-9356-7

  20. Wu ZG, Shi P, Su H, Chu J (2011) Passivity analysis for discretetime stochastic Markovian jump neural networks with mixed time delays. IEEE Trans Neural Netw 22:1566–1575

    Article  Google Scholar 

  21. Wu ZG, Shi P, Su H, Chu J (2014) Asynchronous \(L_2-L_{\infty }\) filtering for discrete-time stochastic Markov jump systems with randomly occurred sensor nonlinearities. Automatica 50:180–186

    Article  MathSciNet  MATH  Google Scholar 

  22. Wu ZG, Shi P, Su H, Chu J (2013) Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled data. IEEE Trans Cybern 43:1796–1806

    Article  Google Scholar 

  23. Chandrasekar A, Rakkiyappan R, Rihan FA, Lakshmanan S (2014) Exponential synchronization of Markovian jumping neural networks with partly unknown transition probabilities via stochastic sampled-data control. Neurocomputing 133:385–398

    Article  Google Scholar 

  24. Rakkiyappan R, Chandrasekar A, Park JH, Kwon OM (2014) Exponential synchronization criteria for Markovian jumping neural networks with time-varying delays and sampled-data control. Nonlinear Anal 14:16–37

    MathSciNet  MATH  Google Scholar 

  25. Wu SL, Li KL, Huang TZ (2011) Global dissipativity of delayed neural networks with impulses. J Frankl Inst 348:2270–2291

    Article  MathSciNet  MATH  Google Scholar 

  26. Guo Z, Wang J, Yan Z (2013) Global exponential dissipativity and stabilization of memristor-based recurrent neural networks with time-varying delays. Neural Netw 48:158–172

    Article  MATH  Google Scholar 

  27. Chen Y, Li W, Bi W (2009) Improved results on passivity analysis of uncertain neural networks with time-varying discrete and distributed delay. Neural Process Lett 30:155–169

    Article  Google Scholar 

  28. Balasubramaniam P, Nagamani G, Rakkiyappan R (2010) Global passivity analysis of interval neural networks with discrete and distributed delays of neutral type. Neural Process Lett 32:109–130

    Article  Google Scholar 

  29. Xiao J, Zeng Z, Shen W (2015) Passivity analysis of delayed neural networks with discontinuous activations. Neural Process Lett 42:215–232

    Article  Google Scholar 

  30. Rakkiyappan R, Chandrasekar A, Cao J (2014) Passivity and passification of memristor-based recurrent neural networks with additive timevarying delays. IEEE Trans Neural Netw Learn Syst. doi:10.1109/TNNLS.2014.2365059

  31. Sun Y, Cui BT (2008) Dissipativity analysis of neural networks with time-varying delays. Int J Autom Comput 05:290–295

    Article  Google Scholar 

  32. Xu S, Zheng WX, Zou Y (2009) Passivity analysis of neural networks with time-varying delays. IEEE Trans Circuits Syst II 56:325–329

    Article  Google Scholar 

  33. Lee W, Park P (2014) Second-order reciprocally convex approach to stability of systems with interval time-varying delays. Appl Math Comput 229:245–253

    Article  MathSciNet  Google Scholar 

  34. Park P, Ko JW, Jeong C (2011) Reciprocally convex approach to stability of systems with time-varying delays. Automatica 47:235–238

    Article  MathSciNet  MATH  Google Scholar 

  35. Chen Y, Bi W, Li W, Wu Y (2010) Less conservative results of state estimation for neural networks with time-varying delay. Neurocomputing 73:1324–1331

    Article  Google Scholar 

  36. Song Q (2008) Exponential stability of recurrent neural networks with both time-varying delays and general activation functions via LMI approach. Neurocomputing 71:2823–2830

    Article  Google Scholar 

  37. Sun J, Liu GP, Chen J, Rees D (2009) Improved stability criteria for neural networks with time-varying delay. Phys Lett A 373:342–348

    Article  MATH  Google Scholar 

  38. Tian J, Zhong S (2011) Improved delay-dependent stability criterion for neural networks with time-varying delay. Appl Math Comput 217:10278–10288

    Article  MathSciNet  MATH  Google Scholar 

  39. Shi K, Zhong S, Zhu H, Liu X, Zeng Y (2015) New delay-dependent stability criteria for neutral-type neural networks with mixed random time-varying delays. Neurocomputing. doi:10.1016/j.neucom.2015.05.035i

Download references

Acknowledgments

The work of authors was supported by UGC-BSR Research Start-Up-Grant, New Delhi, India, under the sanctioned No. F. 20-1/2012 (BSR)/20-5(13)/2012(BSR).

Author information

Authors and Affiliations

  1. Department of Mathematics, Gandhigram Rural Institute - Deemed University, Gandhigram, Tamil Nadu, 624 302, India

    G. Nagamani & T. Radhika

Authors
  1. G. Nagamani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Radhika
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Nagamani.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nagamani, G., Radhika, T. Dissipativity and Passivity Analysis of Markovian Jump Neural Networks with Two Additive Time-Varying Delays. Neural Process Lett 44, 571–592 (2016). https://doi.org/10.1007/s11063-015-9482-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-015-9482-x

Keywords

Search

Navigation