$H_{\infty }$ Estimation for Markovian Jump Neural Networks With Quantization, Transmission Delay and Packet Dropout

Abstract

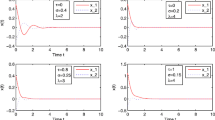
This paper is concerned with the problem of robust $H_{\infty }$ estimation for a class of Markovian jump neural networks with norm-bounded parameter uncertainties, time-varying delay and limited communication capacity including signal transmission delay, measurement quantization and data packet dropout, which occur simultaneously in the same networked control system framework. Our objective is to design mode-dependent $H_{\infty }$ filter in the network environment in order to ensure the filtering error system is not only exponentially mean-square stable, but also satisfies a prescribed $H_{\infty }$ norm level for the limited communication capacity and for all admissible uncertainties. We use the delay system method to deal with signal transmission delay and data packet dropout, utilize the sector bound approach to handle measurement quantization. We also construct a comprehensive stochastic Lyapunov–Krasovskii functional to show the inherent mode-dependent state delays in the neural networks itself and the network-induced signal transmission delay. The free-weighting matrix technique and a set of strict linear matrix inequalities are employed to derive novel conditions for the desired mode-dependent $H_{\infty }$ filter. A numerical example is provided to verify the effectiveness and usefulness of the obtained main results.