Characterization of Graph-Based Hierarchical Watersheds: Theory and Algorithms

Abstract

Watershed is a well-established clustering and segmentation method. In this article, we aim to achieve a better theoretical understanding of the hierarchical version of the watershed operator. More precisely, we propose a characterization of hierarchical watersheds in the framework of edge-weighted graphs. The proposed characterization leads to an efficient algorithm to recognize hierarchical watersheds.

Appendices

Proof of Property 7

Property 7

Let ${\mathcal {H}}$ be a hierarchy on V. The hierarchy ${\mathcal {H}}$ is a hierarchical watershed of (G, w) if and only if there exists an altitude ordering $\prec$ for w and an extinction map $\epsilon$ for $\prec$ such that

• 1. $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$; and

• 2. for any edge u in $E_\prec$, we have: $\varPhi ({\mathcal {H}})(u) = \min \{\epsilon (R)$ such that R is a child of $R_u\}$.

To prove Property 7, we first present a result established in [6] and other auxiliary lemmas.

Let $\prec$ be an altitude ordering for w, let ${\mathcal {B}}_{\prec }$ be the binary partition hierarchy by $\prec$ and let ${\mathcal {S}} = (M_1, \ldots , M_n)$ be a sequence of minima of w. Let u be a building edge for $\prec$ and let X be the region of ${\mathcal {B}}_{\prec }$ whose building edge is u. The persistence value of u(for$\prec$and${\mathcal {S}}$) is the minimum of the extinction values of the children of X. Let $\rho$ be the map from the building edges for $\prec$ into $\mathbb {R}$ such that, for any building edge u for $\prec$, $\rho (u)$ is the persistence value of u. We say that $\rho$is the persistence map (for$\prec$and${\mathcal {S}}$). We denote by $B_i$ the set of building edges for $\prec$ whose persistence value is lower than or equal to i.

Definition 15

(Hierarchy induced by an altitude ordering and a sequence of minima [6]) Let $\prec$ be an altitude ordering for w, let ${\mathcal {S}}=(M_1, \ldots , M_n)$ be a sequence of minima of w, and let $\rho$ be the persistence map for $\prec$ and ${\mathcal {S}}$. The sequence of partitions $(CC(V,B_0), \ldots , CC(V,B_{n-1}))$ is a hierarchy called the hierarchy induced by $\prec$and ${\mathcal {S}}$.

Lemma 16

(Property 12 of [6]) Let ${\mathcal {S}} = (M_1, \ldots , M_n)$ be a sequence of minima of w and let ${\mathcal {H}}$ be a hierarchy on V. The hierarchy ${\mathcal {H}}$ is a hierarchical watershed of (G, w) for ${\mathcal {S}}$ if and only if there exists an altitude ordering $\prec$ such that ${\mathcal {H}}$ is the hierarchy induced by $\prec$ and ${\mathcal {S}}$.

Lemma 17

Let $\prec$ be an altitude ordering for w and let $\epsilon$ be an extinction map for $\prec$. Let X and Y be two regions of ${\mathcal {B}}_{\prec }$. If $X \subseteq Y$, then $\epsilon (X) \le \epsilon (Y)$.

Proof

Since ${\mathcal {B}}_{\prec }$ is a hierarchy, we can affirm that, for any two regions Y and Z of ${\mathcal {B}}_{\prec }$, if $Y \subseteq Z$, then all minima of w included in Y are also included in Z and, therefore, $\epsilon (Y) \le \epsilon (Z)$. $\square$

From the results established in [26], we can state the following lemma.

Lemma 18

Let ${\mathcal {B}}$ be a binary partition hierarchy of (G, w). Then, any minimum of w is a region of ${\mathcal {B}}$.

Lemma 19

Let $\prec$ be an altitude ordering on the edges of G for w, let ${\mathcal {S}} = (M_1, \ldots , M_n)$ be a sequence of minima of w and let $\rho$ be the persistence map for $\prec$ and ${\mathcal {S}}$. The range of $\rho$ is $\{0, \ldots , n-1\}$.

Proof

Let $\epsilon$ be the extinction map for $\prec$ and ${\mathcal {S}}$. We will prove that (1) for any building edge u for $\prec$, $\rho (u)$ is in $\{0, \ldots , n-1\}$, and that, (2) for any i in $\{0, \ldots , n-1\}$, there is a building edge u for $\prec$ such that $\rho (u)=i$.

• 1. $\{0, \ldots , n-1\} \subseteq range(\rho )$. First, we prove that 0 is in $range(\rho )$. By Property 6, there is a region X of ${\mathcal {B}}_{\prec }$ whose extinction value is zero. Therefore, the persistence value of the building edge u of the parent of X is equal to zero: $\rho (u)=0$. Now, we will prove that any i in $\{1, \ldots , n-1\}$ is in $range(\rho )$. Let i be a value in $\{1, \ldots , n-1\}$. By Lemma 18, the minimum $M_i$ is a region of ${\mathcal {B}}_\prec$. Then, there is a region of ${\mathcal {B}}_\prec$ whose extinction value is i. Let X be the largest region of ${\mathcal {B}}_\prec$ whose extinction value is i. We can say that $X \ne V$ because $M_n$ is included in V and, therefore, $\epsilon (V) = n$. Let Z be the parent of X. We can infer that the extinction value $\epsilon (Z)$ of Z is strictly greater than i. Therefore, there is a minimum $M_j$ with $j>i$ included in the sibling of X. Hence, the extinction value of sibling(X) is also strictly greater than i. Then, the persistence value of the building edge of Z, being the minimum of the extinction value of its children, is i.

• 2. $range(\rho ) \subseteq \{0, \ldots , n-1\}$. Let u be an edge in $E_\prec$. By Property 6 (statement 1), and as the persistence value of u is equal to the extinction value of a child of $R_u$, we have that $\rho (u)$ is in $\{0, \ldots , n\}$. Moreover, the persistence value $\rho (u)$ of u is lower than n because, if the extinction value of one child X of $R_u$ is n, then the minimum $M_n$ is included in X and $M_n$ is not included in sibling(X), which implies that the extinction value of sibling(X) is strictly lower than n. Therefore, since $\rho (u) = min\{\epsilon (X), \epsilon (sibling(X))\}$, the persistence value of u is strictly lower than n. Thus, we have that $range(\rho ) \subseteq \{0, \ldots , n-1\}$.$\square$

Lemma 20

Let $\prec$ be an altitude ordering for w, let ${\mathcal {S}}=(M_1, \ldots , M_n)$ be a sequence of minima of w and let $\rho$ be the persistence map for $\prec$ and ${\mathcal {S}}$. Let ${\mathcal {H}}$ be the hierarchy induced by $\prec$ and ${\mathcal {S}}$. For any edge u in $E_\prec$, we have $\varPhi ({\mathcal {H}})(u)=\rho (u)$.

Proof

By Definition 15, the hierarchy ${\mathcal {H}}$ is the sequence $(CC(V,B_0), \ldots , CC(V,B_{n-1}))$ such that, for any i in $\{0, \ldots , n-1\}$, $B_i$ is the set of building edges for $\prec$ whose persistence values are lower than or equal to i. Let $u=\{x,y\}$ be a building edge for $\prec$ and let i be the persistence value of u. We can say that x and y are in the same region of $CC(V,B_i)$ but in distinct regions of $CC(V,B_{i-1})$ if $i\ne 0$. Therefore, since $CC(V,B_i)$ is the i-th partition of ${\mathcal {H}}$, by the definition of saliency maps, we have $\varPhi ({\mathcal {H}})(u) = i$. $\square$

The following lemma, established in [9], links MSTs and QFZ hierarchies.

Lemma 21

(Theorem 4 of [9]) A subgraph $G'$ of G is a MST of (G, w) if and only if:

• 1. the QFZ hierarchy of $G'$ and G are the same; and

• 2. the graph $G'$ is minimal for statement 1, i.e. for any subgraph $G''$ of $G'$, if the quasi-flat zone hierarchy of $G''$ for w is the one of G for w, then we have $G''=G'$.

Lemma 22

Let $\prec$ be an altitude ordering for w and let ${\mathcal {S}}=(M_1, \ldots , M_n)$ be a sequence of minima of w. Let ${\mathcal {H}}$ be the hierarchy induced by $\prec$ and ${\mathcal {S}}$. Then, $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$.

Proof

Let $\alpha$ denote the sum of the weight of the edges in $E_\prec$ in the map $\varPhi ({\mathcal {H}})$: $\alpha = \sum _{e\in E_\prec }\varPhi ({\mathcal {H}})(e)$. Let $\rho$ be the persistence map for $\prec$ and ${\mathcal {S}}$. By Lemma 20, we can affirm that, for any edge u in $E_\prec$, we have $\varPhi ({\mathcal {H}})(u) = \rho (u)$. Hence, we have $\alpha = \sum _{e\in E_\prec }\rho (e)$. We will first prove that $\alpha$ is precisely $0 + 1 + \ldots + n-1$. We know that, for any edge u in $E_\prec$:

• 1. if u is a watershed-cut edge for $\prec$, then each child of $R_u$ contains at least one minimum of w. Therefore, the extinction values of both children of $R_u$ is nonzero, and, consequently, the persistence value $\rho (u)$ of u is nonzero.

• 2. otherwise, if u is not a watershed-cut edge for $\prec$, then there exists a child X of $R_u$ such that there is no minimum of w included in X. Therefore, the extinction value of X is zero. Since the extinction value of sibling(X) is at least zero by Lemma 35 (statement 1), the persistence value $\rho (u)$ of u, being the minimum between the extinction values of X and sibling(X), is also zero.

Hence, since there are $n-1$ watershed-cut edges for $\prec$, and since only the watershed-cut edges for $\prec$ have nonzero persistence values, we can conclude that, for any i in $\{1, \ldots , n-1\}$, there is exactly one edge u in $E_\prec$ such that $\rho (u) = i$. Hence, $\alpha = \sum _{e\in E_\prec }\rho (e)=0 + 1 + \ldots + n-1$.

Now, in order to prove that $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$, we will prove that, for any MST $G'$ of $(G,\varPhi ({\mathcal {H}}))$, the sum of the weight of the edges in $G'$ is greater than or equal to $\alpha$. Let $G'$ be a MST of $(G, \varPhi ({\mathcal {H}}))$. As $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}))$, by the condition 1 of Lemma 21, we have that G and $G'$ have the same quasi-flat zones hierarchies: $\mathcal {QFZ}(G, \varPhi ({\mathcal {H}}))= \mathcal {QFZ}(G', \varPhi ({\mathcal {H}}))$. As $\varPhi ({\mathcal {H}})$ is the saliency map of ${\mathcal {H}}$, we have that ${\mathcal {H}} = \mathcal {QFZ}(G, \varPhi ({\mathcal {H}}))$. Therefore, ${\mathcal {H}} = \mathcal {QFZ}(G', \varPhi ({\mathcal {H}}))$. Let i be a value in $\{1, \ldots , n-1\}$. Since $\sum _{e\in E_\prec }\varPhi ({\mathcal {H}})(e)=0 + 1 + \ldots + n-1$, we can say that $\{1, \ldots , n-1\}$ is a subset of the range of $\varPhi ({\mathcal {H}})$. Therefore, ${\mathcal {H}}$ is composed of at least n distinct partitions. Let ${\mathcal {H}}$ be the sequence $(\mathbf{P }_0, \ldots , \mathbf{P }_{n-1}, \ldots )$. Since the partitions $\mathbf{P }_{i}$ and $\mathbf{P }_{i-1}$ are distinct, then there exists a region in $\mathbf{P }_i$ which is not in $\mathbf{P }_{i-1}$. Therefore, there is a region X of $\mathbf{P }_i$ which is composed of several regions $\{R_1, R_2, \ldots \}$ of $\mathbf{P }_{i-1}$. Then, there are two adjacent vertices x and y such that x and y are in distinct regions in $\{R_1, R_2, \ldots \}$. Let x and y be two adjacent vertices such that x and y are in distinct regions in $\{R_1, R_2, \ldots \}$. Hence, the lowest j such that x and y belong to the same region of $\mathbf{P }_j$ is i. Thus, there exists an edge $u=\{x,y\}$ in $E_\prec$ such that $\varPhi ({\mathcal {H}})(u)=i$. Hence, the sum of the weight of the edges of $G'$ is at least $1 + \ldots + n-1$, which is equal to $\alpha$. Therefore, the graph $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$. $\square$

Proof of Property 7

We first prove the forward implication of this property. Let ${\mathcal {H}}$ be a hierarchical watershed of (G, w). Then, there is a sequence ${\mathcal {S}}$ of minima of w such that ${\mathcal {H}}$ is the hierarchical watershed of (G, w) for ${\mathcal {S}}$. Let ${\mathcal {S}}$ be the sequence of minima of w such that ${\mathcal {H}}$ is the hierarchical watershed of (G, w) for ${\mathcal {S}}$. By Lemma 16, there is an altitude ordering $\prec$ such that ${\mathcal {H}}$ is the hierarchy induced by $\prec$ and ${\mathcal {S}}$. Let $\prec$ be an altitude ordering such that ${\mathcal {H}}$ is the hierarchy induced by $\prec$ and ${\mathcal {S}}$. Then, by Lemma 22, $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$. We will now prove the second statement of Property 7. By Lemma 20, for any edge u in $E_\prec$, $\varPhi ({\mathcal {H}})(u)$ is equal to the persistence value $\rho (u)$ of u for $\prec$ and ${\mathcal {S}}$. By the definition of persistence values, for edge u in $E_\prec$, the persistence value of u for $\prec$ and ${\mathcal {S}}$ is the minimum extinction value of the children of $R_u$. Therefore, we can conclude that, for edge u in $E_\prec$, $\varPhi ({\mathcal {H}})(u) = \min \{\epsilon (R)$ such that R is a child of $R_u\}$, where $\epsilon$ is the extinction map for $\prec$ and ${\mathcal {S}}$. Hence, there exists an extinction map $\epsilon$ such that, for edge u in $E_\prec$, $\varPhi ({\mathcal {H}})(u) = \min \{\epsilon (R)$ such that R is a child of $R_u\}$.

We will now prove the backward implication of Property 7. Let ${\mathcal {H}}$ be a hierarchy on V such that there exists an altitude ordering $\prec$ for w and an extinction map $\epsilon$ for $\prec$ such that:

• 1. $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$; and

• 2. for any edge u in $E_\prec$, we have: $\varPhi ({\mathcal {H}})(u) = \min \{\epsilon (R)$ such that R is a child of $R_u\}$.

Let $G'$ denote the graph $(V,E_\prec )$. By Lemma 21 (statement 1), as $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}))$, we have that $G'$ and G have the same quasi-flat zones hierarchies (for $\varPhi ({\mathcal {H}})$): $\mathcal {QFZ}(G',\varPhi ({\mathcal {H}})) = \mathcal {QFZ}(G,\varPhi ({\mathcal {H}}))$. Let $\rho$ be the persistence map for $\prec$ and ${\mathcal {S}}$. By the definition of persistence values, we can affirm that, for any edge u in $E_\prec$, we have $\varPhi ({\mathcal {H}})(u) = \rho (u)$. Hence, we can say that $\mathcal {QFZ}(G',\varPhi ({\mathcal {H}})) = \mathcal {QFZ}(G',\rho ))$. Let ${\mathcal {H}}'$ be the hierarchy induced by $\prec$ and ${\mathcal {S}}$. By Lemma 22, $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}'))$. Hence, by Lemma 21, $G'$ and G have the same quasi-flat zones hierarchies (for $\varPhi ({\mathcal {H}}')$): $\mathcal {QFZ}(G',\varPhi ({\mathcal {H}}')) = \mathcal {QFZ}(G,\varPhi ({\mathcal {H}}'))$. By Lemma 20, for edge u in $E_\prec$, we have $\varPhi ({\mathcal {H}}')(u) = \rho (u)$, which is equal to $\varPhi ({\mathcal {H}})(u)$ as stated previously. Thus, $\mathcal {QFZ}(G',\varPhi ({\mathcal {H}}')) = \mathcal {QFZ}(G',\varPhi ({\mathcal {H}}))$ and, consequently, ${\mathcal {H}}$ and ${\mathcal {H}}'$ are equal. By Lemma 16, ${\mathcal {H}}'$ is a hierarchical watershed of (G, w). Therefore, ${\mathcal {H}}$ is a hierarchical watershed of (G, w). $\square$

Proof of Theorem 5

Theorem 5

Let ${\mathcal {H}}$ be a hierarchy on V and let $\prec$ be a lexicographic ordering for (w, f). The hierarchy ${\mathcal {H}}$ is a hierarchical watershed of (G, w) if and only if $\varPhi ({\mathcal {H}})$ is one-side increasing for $\prec$.

Let ${\mathcal {H}}$ be a hierarchy on V. By Lemma 4, ${\mathcal {H}}$ is a hierarchical watershed of (G, w) if and only if there is an altitude ordering for w such that the saliency map $\varPhi ({\mathcal {H}})$ of ${\mathcal {H}}$ is one-side increasing for $\prec$. In order to prove Theorem 5, we will prove in the following lemma that, if the saliency map $\varPhi ({\mathcal {H}})$ is one-side increasing for an altitude ordering for w, then $\varPhi ({\mathcal {H}})$ is one-side increasing for any lexicographic ordering for $(w, \varPhi ({\mathcal {H}}))$.

Given a map f from E into $\mathbb {R}$, we say that fis a saliency map if there is an hierarchy ${\mathcal {H}}$ on V such that f is the saliency map of ${\mathcal {H}}$.

Lemma 23

Let f be a saliency map and let $\prec _f$ be a lexicographic ordering for (w, f). If there exists an altitude ordering $\prec$ for w such that f is one-side increasing for $\prec$, then f is one-side increasing for $\prec _f$.

Let $\prec$ be an ordering on E and let $(u_1, \ldots , u_{|E|})$ be the sequence of edges in E such that, for any i in $\{1, \ldots , |E|-1\}$, we have $u_{i} \prec u_{i+1}$. This sequence $(u_1, \ldots , u_{|E|})$ is called the sequence (of edges) induced by$\prec$. In order to prove Lemma 23, we first introduce the notion of critical rank and the notion of switch in the context of lexicographic orderings, and other auxiliary lemmas.

Definition 24

(Critical rank) Let f be a saliency map and let $\prec$ be an altitude ordering for w. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Let k be a value such that $u_{k} \prec u_{k+1}$ and such that $w(u_k) = w(u_{k+1})$ and $f(u_k) \ge f(u_{k+1})$. We say that kis a critical rank forfand$\prec$.

Definition 25

(Switch) Let f be a saliency map and let $\prec$ be an altitude ordering for w. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Let k be a critical rank for f and $\prec$, and let $\prec _k$ be the ordering such that $(u_1, \ldots , u_{k+1}, u_k, \ldots , u_{|E|})$ is the sequence induced by $\prec _k$. We say that $\prec _k$ is a switch of $\prec$ for f (and k).

Lemma 26

Let f be a saliency map, let $\prec$ be an altitude ordering for w and let $\prec '$ be a switch of $\prec$ for f. Then, $\prec '$ is an altitude ordering for w.

Proof

Let $\prec '$ be the switch of $\prec$ for a critical rank k for f and $\prec$. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Then, $(u_1, \ldots , u_{k+1}, u_k, \ldots , u_{|E|})$ is the sequence induced by $\prec '$. We may affirm that, for any edge v different from $u_{k+1}$, if $v \prec u_k$ (resp. $u_k \prec v$) then $v \prec ' u_k$ (resp. $u_k \prec ' v$). Similarly, for any edge v different from $u_{k}$, if $v \prec u_{k+1}$ (resp. $u_{k+1} \prec v$) then $v \prec ' u_{k+1}$ ($u_{k+1} \prec ' v$). Finally, for any two edges u and v such that $\{u,v\} \cap \{u_{k}, u_{k+1}\} = \emptyset$, if $u \prec v$ (resp. $v \prec u$), then $u \prec ' v$ (resp. $v \prec ' u$). Hence, for any two edges u and v such that $w(u) < w(v)$, by the definition of critical rank, we may say that $\{u,v\} \ne \{u_k, u_{k+1}\}$ and, consequently, as $u \prec v$, then $u \prec ' v$. Hence, $\prec '$ is an altitude ordering for w. $\square$

Lemma 27

Let $\prec$ be an altitude ordering for w and let f be a saliency map. Let $\prec '$ be a lexicographic ordering for (w, f). There exists a sequence $(\prec _0, \prec _1, \ldots , \prec _\ell )$ of altitude orderings for w such that $\prec _0$ is equal to $\prec$, $\prec _\ell$ is equal to $\prec '$ and, for any i in $\{1, \ldots , \ell \}$, $\prec _i$ is a switch of $\prec _{i-1}$.

Proof

Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$ and let $(u'_1, \ldots , u'_{|E|})$ be the sequence induced by $\prec '$. Let k be the smallest value such that $u_k \ne u'_k$. In this case, there is an $i > k$ such that $u'_k = u_i$. As $\prec '$ is a lexicographic ordering for (w, f), for any edge $u_j$ such that $k < j \le i$, we have $f(u_j) \ge f(u_{j-1})$. Hence, there is a sequence S of switches of $\prec$ for critical ranks ranging from $i-1$ to k such that, in the last ordering $\prec ^*$ of the sequence S, the edge with rank k for the ordering $\prec ^*$ is precisely the edge $u'_k$. Let $(u^*_1, \ldots , u^*_{|E|})$ be the sequence induced by $\prec ^*$. We conclude that, for any $q \le k$, we have $u^*_q = u'_q$. Hence, the smallest value m such that $u^*_m \ne u'_m$ is strictly greater than k. By performing this procedure iteratively (like the bubble sort algorithm), the resulting ordering converge to $\prec '$. $\square$

Lemma 28

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. Let $v_1$ and $v_2$ be two edges of E. If $f(v_1)$ is equal to $f(v_2)$, then neither $v_1$ nor $v_2$ is a watershed-cut edge for $\prec$.

Proof

Since f is one-side increasing for $\prec$, by Definition 3, we have $\{f(u) \mid u \in E_\prec \} = \{0, \ldots , n-1\}$ and we have that, for any edge u in $E_\prec$, f(u) is greater than 0 if and only if u is a watershed-cut edge for $\prec$. Since w has n minima, there are $n-1$ watershed-cut edges for $\prec$. Hence, the watershed-cut edges for $\prec$ have pairwise distinct edge weights ranging from 1 to $n-1$. Therefore, neither $v_1$ nor $v_2$ is a watershed-cut edge for $\prec$. $\square$

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. By Lemma 26, every switch of $\prec$ is an altitude ordering for w. By Lemma 27, any lexicographic ordering for (w, f) can be obtained by a sequence of switches starting from $\prec$. Hence, to prove Lemma 23, we can simply prove that f is one-side increasing for any switch of $\prec$. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Then, $(u_1, \ldots , u_{k+1}, u_k, \ldots , u_{|E|})$ is the sequence induced by $\prec '$. In order to prove that f is one-side increasing for the switch $\prec '$ for k, we should consider the following cases:

• 1. Neither $u_{k}$ nor $u_{k+1}$ is a building edge for $\prec$;

• 2. Both $u_{k}$ and $u_{k+1}$ are building edges for $\prec$ and $R_{u_{k}} \cap R_{u_{k+1}} = \emptyset$;

• 3. Both $u_{k}$ and $u_{k+1}$ are building edges for $\prec$ and $R_{u_{k}} \subset R_{u_{k+1}}$;

• 4. Only $u_{k+1}$ is a building edge for $\prec$; and

• 5. Only $u_{k}$ is a building edge for $\prec$.

Lemmas 30, 31, 32, 33 and 34 prove that, for each of those five cases, the saliency map f is one-side increasing for the switch $\prec '$ for k. Before considering those five cases, we first present the following auxiliary lemma.

Lemma 29

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. Let $\prec '$ be an altitude ordering for w such that the set of building edges for $\prec '$ is equal to the set of building edges for $\prec$ and such that the set of regions of ${\mathcal {B}}_\prec$ is equal to the set of regions of ${\mathcal {B}}_{\prec '}$. Then, f is one-side increasing for $\prec '$.

Proof

In the definition of one-side increasing maps (Definition 3), the three conditions for f to be one-side increasing for $\prec$ take into consideration only the weight of the building edges for $\prec$ and the parenthood relationship between the regions of $\prec$. Hence, as the set of building edges for $\prec '$ is the same set of building edges for $\prec$ and as they have the same set of regions, we can conclude that the three conditions of Definition 3 for f to the one-side increasing for $\prec '$ are satisfied. $\square$

Lemma 30

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Let k be a critical rank for f and $\prec$ such that neither $u_{k}$ nor $u_{k+1}$ is a building edge for $\prec$. Then, f is one-side increasing for the switch $\prec '$ for k.

Proof

Let $(\mathbf{B }_0, \mathbf{B }_1, \ldots , \mathbf{B }_{|E|})$ be the sequence of partitions (of V) such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }_i$ is the i-partition by the ordering $\prec$ (as defined in Sect. 3.1). Let $(\mathbf{B }'_0, \mathbf{B }'_1, \ldots , \mathbf{B }'_{|E|})$ be the sequence of partitions such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }'_i$ is the i-partition by the ordering $\prec '$. We will prove that neither $u_k$ nor $u_{k+1}$ is a building edge for $\prec '$.

We first prove that $u_{k+1}$ is not a building edge for $\prec '$. By the definition of binary partition hierarchy and, as neither $u_{k}$ nor $u_{k+1}$ is a building edge for $\prec$, we may say that:

• I the partition $\mathbf{B }_k$ is equal to the partition $\mathbf{B }_{k-1}$, and

• II the partition $\mathbf{B }_{k+1}$ is equal to the partition $\mathbf{B }_{k}$,

• III which implies that $\mathbf{B }_{k-1}=\mathbf{B }_{k}=\mathbf{B }_{k+1}$.

Let $u_k=\{s,r\}$ and $u_{k+1} = \{x,y\}$. By the definition of switch, the sequence $(u_1, \ldots , u_{k+1}, u_k, \ldots , u_{|E})$ is the sequence induced by $\prec '$. We may infer that, for any $i < k$, the i-partition by the ordering $\prec '$ is equal to the i-partition by the ordering $\prec$. Hence, as $u_{k+1}$ is the edge of rank k for $\prec '$ and since $\mathbf{B }'_{k-1}=\mathbf{B }_{k-1}$, the k-partition for the ordering $\prec '$ is the partition $\mathbf{B }'_k = \{ \mathbf{B }_{k-1}^y \cup \mathbf{B }_{k-1}^x \} \cup (\mathbf{B }_{k-1} {\setminus } \{\mathbf{B }_{k-1}^x, \mathbf{B }_{k-1}^y\})$. By the statement I, $\mathbf{B }_{k-1} = \mathbf{B }_{k}$, which implies that $\mathbf{B }'_k = \{ \mathbf{B }_{k}^y \cup \mathbf{B }_{k}^x \} \cup (\mathbf{B }_{k} {\setminus } \{\mathbf{B }_{k}^x, \mathbf{B }_{k}^y\})$. Therefore, we have that:

• IV $\mathbf{B }'_k$ is equal to the partition $\mathbf{B }_{k+1}$

As $\mathbf{B }_{k+1}=\mathbf{B }_{k}=\mathbf{B }_{k-1}$ by statement III, we have that

• V $\mathbf{B }'_k=\mathbf{B }_{k+1} = \mathbf{B }_{k-1}=\mathbf{B }'_{k-1}$

By statement V, as $\mathbf{B }'_k = \mathbf{B }'_{k-1}$, we conclude that $u_{k+1}$ is not a building edge for $\prec '$.

We now prove that $u_k$ is not a building edge for $\prec '$. As $u_k$ is the edge of rank $k+1$ for $\prec '$, the $k+1$-partition for the ordering $\prec '$ is the partition $\mathbf{B }'_{k+1} = \{ \mathbf{B }_{k}^{'s} \cup \mathbf{B }_{k}^{'r} \} \cup (\mathbf{B }'_{k} {\setminus } \{\mathbf{B }_{k}^{'s}, \mathbf{B }_{k}^{'r}\})$. By statement V, we have $\mathbf{B }'_k=\mathbf{B }'_{k-1}$. Since $\mathbf{B }'_{k-1}=\mathbf{B }_{k-1}$, then, by statement III, we have that $\mathbf{B }'_k = \mathbf{B }_{k-1}$. Therefore, we conclude that:

• VI $\mathbf{B }'_{k+1} = \{ \mathbf{B }_{k-1}^s \cup \mathbf{B }_{k-1}^r \} \cup (\mathbf{B }_{k-1} {\setminus } \{\mathbf{B }_{k-1}^s, \mathbf{B }_{k-1}^r\})$

By the definition of $\mathbf{B }'_{k+1}$ in the statement VI, we have:

• VII $\mathbf{B }'_{k+1} = \mathbf{B }_k$

By statement IV, $\mathbf{B }'_k=\mathbf{B }_{k+1}$, and by statement III, $\mathbf{B }_k=\mathbf{B }_{k+1}$. Hence, $\mathbf{B }_k = \mathbf{B }'_k$. Thus, by the statement VII, we conclude that $\mathbf{B }'_{k+1} = \mathbf{B }'_k$. Therefore, $u_k$ is not a building edge for $\prec '$.

Since the sequences induced by the orderings $\prec$ and $\prec '$ are equal for any $i > k+1$, and since $\mathbf{B }'_{k+1} = \mathbf{B }'_k = \mathbf{B }_k = \mathbf{B }_{k+1}$, we may affirm that, $\mathbf{B }_i = \mathbf{B }'_i$ for any $i > k+1$. Therefore, the set of building edges for $\prec$ is equal to the set of building edges for $\prec '$, and the set of partitions and regions of ${\mathcal {B}}_\prec$ is equal to the set of partitions and regions of ${\mathcal {B}}_{\prec '}$. By Lemma 29, f is one-side increasing for $\prec '$. $\square$

Lemma 31

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Let k be a critical rank for f and $\prec$ such that both $u_{k}$ and $u_{k+1}$ are building edges for $\prec$ and such that $R_{u_{k}} \cap R_{u_{k+1}} = \emptyset$. Then, f is one-side increasing for the switch $\prec '$ for k.

Proof

In this proof, we first show that $u_{k+1}$ and $u_k$ are building edges for $\prec '$. Then, we conclude that the partitions of the binary partition hierarchies for $\prec$ and for $\prec '$ are equal, which, by Lemma 29, prove that f is one-side increasing for $\prec '$.

Let $(\mathbf{B }_0, \mathbf{B }_1, \ldots , \mathbf{B }_{|E|})$ be the sequence of partitions (of V) such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }_i$ is the i-partition by the ordering $\prec$. Let $(\mathbf{B }'_0, \mathbf{B }'_1, \ldots , \mathbf{B }'_{|E|})$ be the sequence of partitions such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }'_i$ is the i-partition by the ordering $\prec '$. By the definition of switch, the sequence $(u_1, \ldots , u_{k+1}, u_k, \ldots , u_{|E|})$ is the sequence induced by $\prec '$. As the sequences induced by $\prec$ and by $\prec '$ are equal for any edge with rank $i<k$, we may affirm that:

• I $\mathbf{B }_i = \mathbf{B }'_i$ for any $i<k$

Let $u_k=\{s,r\}$ and $u_{k+1} = \{x,y\}$. As $u_{k}$ and $u_{k+1}$ are building edges for $\prec$, we have that:

• II $\mathbf{B }_{k} \ne \mathbf{B }_{k-1}$, and

• III $\mathbf{B }_{k+1} \ne \mathbf{B }_{k}$

As $u_{k+1}$ is the edge of rank k for $\prec '$, we have that the k-partition for the ordering $\prec '$ is $\mathbf{B }'_k = \{ \mathbf{B }_{k-1}^{'x} \cup \mathbf{B }_{k-1}^{'y} \} \cup (\mathbf{B }'_{k-1} {\setminus } \{\mathbf{B }_{k-1}^{'x}, \mathbf{B }_{k-1}^{'y}\})$. By the statement I, $\mathbf{B }'_{k-1}$ and $\mathbf{B }_{k-1}$ are equal. Then, $\mathbf{B }'_k = \{ \mathbf{B }_{k-1}^x \cup \mathbf{B }_{k-1}^y \} \cup (\mathbf{B }_{k-1} {\setminus } \{\mathbf{B }_{k-1}^x, \mathbf{B }_{k-1}^y\})$.

By definition, we have:

• IV $\mathbf{B }_{k} = \{ \mathbf{B }_{k-1}^s \cup \mathbf{B }_{k-1}^r \} \cup (\mathbf{B }_{k-1} {\setminus } \{\mathbf{B }_{k-1}^s, \mathbf{B }_{k-1}^r\})$, and

• V $\mathbf{B }_{k+1} = \{ \mathbf{B }_{k}^x \cup \mathbf{B }_{k}^y \} \cup (\mathbf{B }_{k} {\setminus } \{\mathbf{B }_{k}^x, \mathbf{B }_{k}^y\})$

By our hypothesis, we have $R_{u_{k}} \cap R_{u_{k+1}} = \emptyset$, which means that the regions $R_{u_{k}}$ and $R_{u_{k+1}}$ of ${\mathcal {B}}_\prec$ (whose building edges are, respectively, $u_k$ and $u_{k+1}$) have no intersection. As $u_k$ is a building edge for $\prec$, we have $R_{u_{k}} = \{ \mathbf{B }_{k-1}^s \cup \mathbf{B }_{k-1}^r \}$. Similarly, as $u_{k+1}$ is a building edge for $\prec$, we have $R_{u_{k+1}} = \{ \mathbf{B }_{k}^x \cup \mathbf{B }_{k}^y \}$. Since $R_{u_{k}} \cap R_{u_{k+1}} = \emptyset$, we have that:

• VI neither x nor y is in the region $\mathbf{B }_{k-1}^s$ (nor in the region $\mathbf{B }_{k-1}^r$), and

• VII neither s nor r is in the region $\mathbf{B }_{k}^x$ (nor in the region $\mathbf{B }_{k}^y$)

By VI and VII, we can conclude that $\mathbf{B }_{k-1}^s$, $\mathbf{B }_{k-1}^r$, $\mathbf{B }_{k}^x$ and $\mathbf{B }_{k}^y$ are all distinct regions of the partition $\mathbf{B }_{k-1}$. Hence, we have:

• VIII $\mathbf{B }_{k}^x = \mathbf{B }_{k-1}^x$, and

• IX $\mathbf{B }_{k}^y = \mathbf{B }_{k-1}^y$

By definition, as $u_{k+1}$ is the edge of rank k for $\prec '$, we have:

• X $\mathbf{B }'_{k} = \{ \mathbf{B }_{k-1}^{'x} \cup \mathbf{B }_{k-1}^{'y} \} \cup (\mathbf{B }'_{k-1} {\setminus } \{\mathbf{B }_{k-1}^{'x}, \mathbf{B }_{k-1}^{'y}\})$

By I and X, we conclude that:

• XI $\mathbf{B }'_{k} = \{ \mathbf{B }_{k-1}^x \cup \mathbf{B }_{k-1}^y \} \cup (\mathbf{B }_{k-1} {\setminus } \{\mathbf{B }_{k-1}^x, \mathbf{B }_{k-1}^y\})$

By VIII, IX and XI, we conclude:

• XII $\mathbf{B }'_{k} = \{ \mathbf{B }_{k}^x \cup \mathbf{B }_{k}^y \} \cup (\mathbf{B }_{k} {\setminus } \{\mathbf{B }_{k}^x, \mathbf{B }_{k}^y\})$

As $\mathbf{B }_{k}^x$ and $\mathbf{B }_{k}^y$ are distinct regions, we may say that $\mathbf{B }'_{k}$ is different from $\mathbf{B }'_{k-1}$. Hence, $u_{k+1}$ is a building edge for $\prec '$.

We now prove that $u_k$ is also a building edge for $\prec '$. As $u_k$ is the edge of rank $k+1$ for $\prec '$, we have that the $(k+1)$-partition for the ordering $\prec '$ is $\mathbf{B }'_{k+1} = \{ \mathbf{B }_{k}^{'s} \cup \mathbf{B }_{k}^{'r} \} \cup (\mathbf{B }'_{k} {\setminus } \{\mathbf{B }_{k}^{'s}, \mathbf{B }_{k}^{'r}\})$. By statement VII, we have that neither s nor r are in the regions $\mathbf{B }_{k}^x$ and $\mathbf{B }_{k}^y$. Hence, by the statement XII, s and r belong to distinct regions of $\mathbf{B }'_{k}$. Therefore, $\mathbf{B }_{k}^{'s} \ne \mathbf{B }_{k}^{'r}$. Consequently, $\mathbf{B }'_{k+1}$ is different from $\mathbf{B }'_{k}$. Hence, $u_k$ is a building edge for $\prec '$.

Moreover, we conclude that $\mathbf{B }'_{k+1} = \mathbf{B }_{k+1}$ because both partitions result from the union of the four distinct regions of $\mathbf{B }_{k-1}$ containing s, r, x and y. Hence, for any $i > k+1$, as the sequences induced by $\prec$ and $\prec '$ are equal, we can conclude that any partition $\mathbf{B }_i$ is equal to the partition $\mathbf{B }'_i$ for any $i > k+1$. Therefore, the building edges for $\prec$ and for $\prec$ are equal, and the set of regions of the binary partitions hierarchies for $\prec$ and for $\prec$ are equal. By Lemma 29, f is one-side increasing for $\prec '$. $\square$

Lemma 32

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Let k be a critical rank for f and $\prec$ such that both $u_{k}$ and $u_{k+1}$ are building edges for $\prec$ and such that $R_{u_{k}} \subset R_{u_{k+1}}$. Then, f is one-side increasing for the switch $\prec '$ for k.

Proof

In this proof, we first show that both $u_k$ and $u_{k+1}$ are building edges for $\prec '$. Then, we conclude that the set of building edges for $\prec$ and for $\prec '$ are equal. Finally, we prove that the three conditions of Definition 3 for f to be one-side increasing for $\prec '$ hold true.

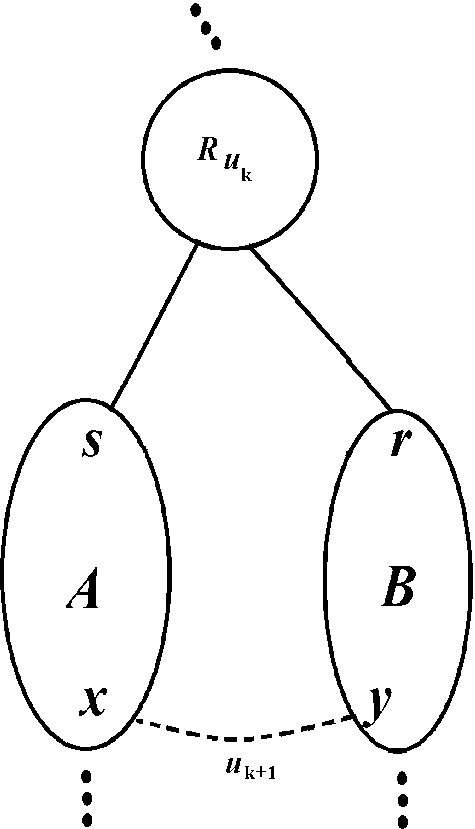
By our hypothesis, the region $R_{u_{k}}$ of ${\mathcal {B}}_\prec$ is a subset of the region $R_{u_{k+1}}$ of ${\mathcal {B}}_\prec$. Let A be the region of ${\mathcal {B}}_\prec$ such that $R_{u_{k+1}} = R_{u_k} \cup A$. Let B and C be the children of $R_{u_k}$. This situation is illustrated in the following figure.

Let $u_k=\{s,r\}$ and $u_{k+1} = \{x,y\}$. As $u_{k+1}$ is a building edge for $\prec$, we conclude that x are y belong to two distinct regions in $\{A,B\}$ or in $\{A,C\}$. Without loss of generality, let us assume that x belongs to A and that y belongs to B. Let $\mathbf{B }_{k-1}$ be the $(k-1)$-partition for $\prec$. We can say that the regions A, B and C belong to $\mathbf{B }_{k-1}$. Moreover, we know that $\mathbf{B }_{k-1}$ is equal to the $(k-1)$-partition for $\prec '$ because, for any $i<k$, the edge of rank i for $\prec$ is also the edge of rank i for $\prec '$. Since $u_{k+1}$ is the edge of rank k for $\prec '$, we can conclude that the k-partition $\mathbf{B }'_k$ for $\prec '$ is the partition $\{A \cup B\} \cup (\mathbf{B }_{k-1} {\setminus } \{A,B\})$. As the region $\{A \cup B\}$ is not in the partition $\mathbf{B }'_{k-1}$, we can conclude that $\mathbf{B }'_{k}$ is different from $\mathbf{B }'_{k-1}$. Hence, $u_{k+1}$ is the building edge of the region $R'_{u_{k+1}} = \{A \cup B\}$ of ${\mathcal {B}}_{\prec '}$. Consequently, $u_{k+1}$ is a building edge for $\prec '$.

We now prove that $u_k$ is also a building edge for $\prec '$. Without loss of generality, let us assume that s belongs to B and that r belongs to C. By our hypothesis, $u_{k}$ is the edge of rank $k+1$ for $\prec '$. In the partition $\mathbf{B }'_k$, we know that s and r belong to distinct regions because s is in $\{A \cup B\}$ and r is in C. Hence, the region $\{A \cup B \cup C\}$ is a region of $\mathbf{B }'_{k+1}$ and we have $\mathbf{B }'_{k+1} \ne \mathbf{B }'_k$. Therefore, $u_k$ is a building edge for $\prec '$. This situation is illustrated in the following figure.

We can infer that the $(k+1)$-partition for $\prec '$ is equal to the $(k+1)$-partition for $\prec$. For $i > k+1$, the edge of rank i for $\prec$ is also the edge of rank i for $\prec '$. Hence, we can conclude that the set of building edges for $\prec$ is equal to the set of building edges for $\prec '$.

Now, we will prove that f is one-side increasing for $\prec '$. To that end, we will demonstrated that the three conditions of the definition of one-side increasing maps (Definition 3) hold true for f.

• 1. We first prove that the condition 1 of Definition  3 holds true for f. Since the set $E_\prec$ of building edges for $\prec$ is equal to the set $E_{\prec '}$ of building edges for $\prec '$, we can conclude that $\{f(u) \mid u \in E_{\prec '}\}$ is equal to $\{f(u) \mid u \in E_\prec \}=\{0, \ldots , n-1\}$. Thus, the first condition for f to be one-side increasing for $\prec '$ holds true.

• 2. We now prove that the condition 2 of Definition 3 holds true for f. In order to prove this condition, we consider four cases: (2.1) both $u_{k}$ and $u_{k+1}$ are watershed-cut edges for $\prec$; (2.2) neither $u_{k}$ nor $u_{k+1}$ is a watershed-cut edge for $\prec$; (2.3) only $u_{k}$ is a watershed-cut for $\prec$; and (2.4) only $u_{k+1}$ is a watershed-cut for $\prec$.

  • (2.1) If both $u_{k}$ and $u_{k+1}$ are watershed-cut edges for $\prec$, then there is at least one minimum of w included in each of the regions A, B and C. Since A and B are the children of $R'_{u_{k+1}}$, we may say that $u_{k+1}$ is a watershed-cut edge for $\prec '$. Since $\{A\cup B\}$ and C are the children of $R'_{u_{k}}$ and since there is at least one minimum included in each of the children of $R'_{u_{k}}$, we may say that $u_{k}$ is a watershed-cut edge for $\prec '$. Hence, both $u_{k}$ and $u_{k+1}$ are watershed-cut edges for $\prec '$.

  • (2.2) If neither $u_{k}$ nor $u_{k+1}$ is a watershed-cut edge for $\prec$, then there are at least two regions among A, B and C that do not include any minimum of w. Hence, there is at least one child of each of the regions $R'_{u_{k}}$ and $R'_{u_{k+1}}$ that do not include any minimum of w. Therefore, neither $u_{k}$ nor $u_{k+1}$ is a watershed-cut edge for $\prec '$.

  • (2.3) If $u_{k}$ is a watershed-cut edge for $\prec$ and if $u_{k+1}$ is not watershed-cut edge for $\prec$, then there is at least one minimum included in each of the regions B and C and there is no minimum included in A. Hence, as A is a child of the region $R'_{u_{k+1}}$ of ${\mathcal {B}}_{\prec '}$ and as there is no minimum of w included in A, $u_{k+1}$ is not a watershed-cut edge for $\prec '$. Since there is at least one minimum included in each of the regions B and C, and since B and C are included in distinct children of the region $R'_{u_{k}}$, we can conclude that $u_{k}$ is a watershed-cut edge for $\prec '$.

  • (2.4) If $u_{k+1}$ is a watershed-cut edge for $\prec$ and if $u_{k}$ is not watershed-cut edge for $\prec$. As k is a critical rank for f and $\prec$, we have that $f(u_{k}) \ge f(u_{k+1})$. However, by the definition of one-side increasing maps (Definition 3), we have $f(u_{k+1}) > 0$ and $f(u_{k})=0$, which contradicts our hypothesis. Therefore, the case where $u_{k+1}$ is a watershed-cut edge for $\prec$ and if $u_{k}$ is not watershed-cut edge for $\prec$ does not happen.

  Therefore, we can conclude that the set of watershed-cut edges for $\prec$ is equal to the set of watershed-cut edges for $\prec '$. Then, the second condition for f to be one-side increasing for $\prec '$ holds true.

• 3. We finally prove that the condition 3 of Definition 3 holds true for f. As k is a critical rank for f and $\prec$, we have that $f(u_{k}) \ge f(u_{k+1})$. We will consider two cases: (3.1) $f(u_{k}) = f(u_{k+1})$; and (3.2) $f(u_{k}) > f(u_{k+1})$.

  • (3.1) If $f(u_{k}) = f(u_{k+1})$, by Lemma 28, neither $u_k$ nor $u_{k+1}$ is a watershed-cut edge for $\prec$. Since neither $u_k$ nor $u_{k+1}$ is a watershed-cut edge for $\prec$, as proven in the case (2.2), neither $u_k$ nor $u_{k+1}$ is a watershed-cut edge for $\prec '$. Hence, there is at least one child of the region $R'_{u_{k}}$ (resp. $R'_{u_{k+1}}$) that does not include any minimum of w. Let Z be the child of $R'_{u_{k}}$ (resp. $R'_{u_{k+1}}$) that does not include any minimum of w. We can infer that there is no watershed-cut edge v for $\prec '$ such that $R_v \subseteq Z$. Then, for any edge v such that $R_v \subseteq Z$, we have $f(v) = 0$. Since $f(u_k) = 0$ (resp. $f(u_{k+1}) = 0$), we can affirm that there is a child Z of $R'_{u_{k}}$ (resp. $R'_{u_{k+1}}$) such that $f(u_k) \ge \vee \{f(v) \mid R_v \subseteq Z\}$ (resp. $f(u_{k+1}) \ge \vee \{f(v) \mid R_v \subseteq Z\}$).

  • (3.2) Let us assume that $f(u_{k}) > f(u_{k+1})$. Since f is one-side increasing for $\prec$, by Definition 3 (statement 3), we conclude that, for any edge v such that v is the building edge of a region included in A, we have $f(u_{k+1}) \ge f(v)$. In the hierarchy ${\mathcal {B}}_{\prec '}$, the region $R'_{u_{k+1}}$ is the parent of A, so the statement 3 of Definition 3 holds true for $R_{u_{k+1}}'$.

    We will now prove that the statement 3 of Definition 3 holds true for $R'_{u_{k}}$. By Definition 3, we know that there is a child Z of $R_{u_k}$ such that for any edge v such that v is the building edge of a region included in Z, we have $f(u_{k}) \ge f(v)$. Let us first assume that $Z = C$. Since C is also a child of the region $R'_{u_k}$ of ${\mathcal {B}}_{\prec '}$, the statement 3 of Definition 3 holds true for $R'_{u_k}$. Now, let us assume that $Z = B$. We will prove that, for the building edge v of any region included in $\{A \cup B \cup R'_{u_{k+1}}\}$, we have $f(u_k) \ge f(v)$. By our assumption $f(u_k) > f(u_{k+1})$, which implies that $f(u_k)$ is greater than the weight of the building edge of $R'_{u_{k+1}}$. By our assumption that $Z=B$, for any edge v such that v is the building edge of a region included in B, we have $f(u_{k}) \ge f(v)$. Moreover, for any edge v such that v is the building edge of a region included in A, we have $f(u_{k}) \ge f(v)$ because $f(u_k) > f(u_{k+1})$ and because A is the child of $R_{u_{k+1}}'$ such that $f(u_{k+1}) \ge \vee \{f(v) \mid R_v \subseteq A\}$. Therefore, for the building edge v of any region included in $\{A \cup B \cup R'_{u_{k+1}}\}$, we have $f(u_k) \ge f(v)$. Consequently, the statement 3 of Definition 3 holds true for $R'_{u_{k}}$. $\square$

Lemma 33

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Let k be a critical rank for f and $\prec$ such that $u_{k+1}$ is a building edge for $\prec$ and such that $u_{k}$ is not a building edge for $\prec$. Then, f is one-side increasing for the switch $\prec '$ for k.

Proof

Let $(\mathbf{B }_0, \mathbf{B }_1, \ldots , \mathbf{B }_{|E|})$ be the sequence of partitions (of V) such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }_i$ is the i-partition by the ordering $\prec$ (as defined in Sect. 3.1). Let $(\mathbf{B }'_0, \mathbf{B }'_1, \ldots , \mathbf{B }'_{|E|})$ be the sequence of partitions such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }'_i$ is the i-partition by the ordering $\prec '$. As the sequences induced by $\prec$ and by $\prec '$ are equal for any edge with rank $i<k$, we may affirm that:

• I. $\mathbf{B }_i = \mathbf{B }'_i$ for any $i<k$

By the definition of binary partition hierarchy and since $u_{k}$ is not a building edge for $\prec$, we may say that:

• II. the partition $\mathbf{B }_k$ is equal to the partition $\mathbf{B }_{k-1}$.

Let $u_k = \{s,r\}$ and $u_{k+1} = \{x,y\}$. Since $\mathbf{B }_k = \mathbf{B }_{k-1}$ and since $\mathbf{B }_k = \{ \mathbf{B }_{k-1}^s \cup \mathbf{B }_{k-1}^r \} \cup (\mathbf{B }_{k-1} {\setminus } \{\mathbf{B }_{k-1}^s, \mathbf{B }_{k-1}^r\})$, we conclude that the regions $\mathbf{B }_{k-1}^s$ and $\mathbf{B }_{k-1}^r$ of the partition $\mathbf{B }_{k-1}$ are equal: $\mathbf{B }_{k-1}^s=\mathbf{B }_{k-1}^r$. By the statement I, we may say that the regions $\mathbf{B }_{k-1}^{'s}$ and $\mathbf{B }_{k-1}^{'r}$ of the partition $\mathbf{B }'_{k-1}$ are equal as well. Hence:

• III. the partition $\mathbf{B }'_k$ is equal to the partition and $\mathbf{B }'_{k-1}$

Therefore, $u_k$ is not a building edge for $\prec '$.

Since $u_{k+1}$ is a building edge for $\prec$, we have that:

• IV. the partition $\mathbf{B }_{k+1}$ is different from the partition $\mathbf{B }_{k}$.

By the statement IV, we conclude that the regions $\mathbf{B }_{k}^x$ and $\mathbf{B }_{k}^y$ of the partition $\mathbf{B }_{k}$ are distinct. By the statement III, we have that $\mathbf{B }'_k = \mathbf{B }'_{k-1}$. Then, by statement I, we have $\mathbf{B }'_k = \mathbf{B }_{k-1}$. Hence, by statement II, we have $\mathbf{B }'_k = \mathbf{B }_k$. Therefore, the regions $\mathbf{B }_{k}^x$ and $\mathbf{B }_{k}^y$ also belong to the partition $\mathbf{B }'_k$. Consequently, since x and y are in distinct regions in the partition $\mathbf{B }'_k$, we conclude that $u_{k+1}$ is a building edge for $\prec '$. Therefore, the set $E_\prec$ of building edges for $\prec$ is equal to the set $E_{\prec '}$ of building edges for $\prec '$.

Moreover, we conclude that $\mathbf{B }'_{k+1} = \mathbf{B }_{k+1}$ because both partitions result from the union of the two distinct regions of $\mathbf{B }_{k-1}$ containing x and y. Hence, for any $i > k+1$, as the edge of rank i for $\prec$ is also the edge of rank i for $\prec '$, we can conclude that any partition $\mathbf{B }_i$ is equal to the partition $\mathbf{B }'_i$. Hence, ${\mathcal {B}}_\prec$ and ${\mathcal {B}}_{\prec }$ have the same set of regions.

Since $E_\prec = E_{\prec '}$ and since ${\mathcal {B}}_\prec$ and ${\mathcal {B}}_{\prec }$ have the same set of regions, by Lemma 29, f is one-side increasing for $\prec '$. $\square$

Lemma 34

Let $\prec$ be an altitude ordering for w and let f be a saliency map such that f is one-side increasing for $\prec$. Let $(u_1, \ldots , u_{|E|})$ be the sequence induced by $\prec$. Let k be a critical rank for f and $\prec$ such that $u_{k}$ is a building edge for $\prec$ and such that $u_{k+1}$ is not a building edge for $\prec$. Then, f is one-side increasing for the switch $\prec '$ for k.

Proof

Let $(\mathbf{B }_0, \mathbf{B }_1, \ldots , \mathbf{B }_{|E|})$ be the sequence of partitions (of V) such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }_i$ is the i-partition by the ordering $\prec$. Let $(\mathbf{B }'_0, \mathbf{B }'_1, \ldots , \mathbf{B }'_{|E|})$ be the sequence of partitions such that, for any i in $\{1, \ldots , |E|\}$, the partition $\mathbf{B }'_i$ is the i-partition by the ordering $\prec '$. As the sequences induced by $\prec$ and by $\prec '$ are equal for any edge with rank $i<k$, we may affirm that:

• I. $\mathbf{B }_i = \mathbf{B }'_i$ for any $i<k$

Since $u_k$ is a building edge for $\prec$, we have that:

• II. $\mathbf{B }_k$ is different from $\mathbf{B }_{k-1}$

Let $u_k = \{s,r\}$ and $u_{k+1} = \{x,y\}$. Since $\mathbf{B }_k \ne \mathbf{B }_{k-1}$, we conclude that s and r are in distinct regions of $\mathbf{B }_{k-1}$. As $u_{k+1}$ is not a building edge for $\prec$, we consider two cases: (1) x and y belong to a unique region of $\mathbf{B }_{k-1}$; and (2) x and y belong to two distinct regions of $\mathbf{B }_{k-1}$.

• (1) Let us consider that x and y belong to a unique region of $\mathbf{B }_{k-1}$. By the statement I, we have $\mathbf{B }'_{k-1} = \mathbf{B }_{k-1}$. Hence, x and y belong to a unique region of $\mathbf{B }'_{k-1}$ and, therefore, $u_{k+1}$ is not a building edge for $\prec '$. We will now prove that $u_{k}$ is a building edge for $\prec '$. Since $u_k$ is a building edge for $\prec$, we have that s and r belong to two distinct regions of the partition $\mathbf{B }_{k-1}$. Since $u_{k+1}$ is not a building edge for $\prec '$, we have $\mathbf{B }'_{k} = \mathbf{B }'_{k-1}$. Then, by the statement I, we have $\mathbf{B }'_{k} = \mathbf{B }'_{k-1} = \mathbf{B }_{k-1}$. Therefore, s and r belong to two distinct regions of the partition $\mathbf{B }'_{k}$. Hence, $u_{k}$ is a building edge for $\prec '$.

  Therefore, the set $E_\prec$ of building edges for $\prec$ is equal to the set $E_{\prec '}$ of building edges for $\prec '$.

  Moreover, we conclude that $\mathbf{B }'_{k+1} = \mathbf{B }_{k+1}$ because both partitions result from the union of the two distinct regions of $\mathbf{B }_{k-1}$ containing s and r. Hence, for any $i > k+1$, as the edge of rank i for $\prec$ is also the edge of rank i for $\prec '$, we can conclude that any partition $\mathbf{B }_i$ is equal to the partition $\mathbf{B }'_i$. Thus, ${\mathcal {B}}_\prec$ and ${\mathcal {B}}_{\prec }$ have the same set of regions.

  Since $E_\prec = E_{\prec '}$ and since ${\mathcal {B}}_\prec$ and ${\mathcal {B}}_{\prec }$ have the same set of regions, by Lemma 29, f is one-side increasing for $\prec '$.

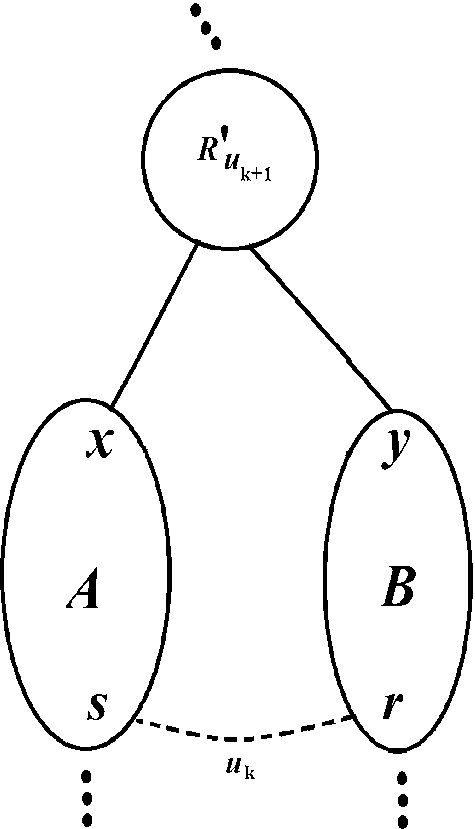
• (2) We now consider that x and y belong to two distinct regions of $\mathbf{B }_{k-1}$. Let A and B be the regions of $\mathbf{B }_{k-1}$ such that $s \in A$ and $r \in B$. Since x and y belong to two distinct regions of $\mathbf{B }_{k-1}$ and since $\mathbf{B }_{k} = \{A \cup B\} \cup (\mathbf{B }_{k-1} {\setminus } \{A,B\})$, we conclude that either x or y is in A, and that either s or r is in B. Without loss of generality, let us assume that $x \in A$ and $y \in B$. This situation is illustrated in the following figure.

  

  Since $u_{k+1}$ is the edge of rank k for the ordering $\prec '$, we can say that the k-partition $\mathbf{B }'_k$ by the ordering $\prec '$ is $\{A \cup B\} \cup (\mathbf{B }'_{k-1} {\setminus } \{A,B\})$ because A and B are the regions of $\mathbf{B }'_{k-1}$ that contain, respectively, x and y. As the region $\{A \cup B\}$ does not belong to the partition $\mathbf{B }'_{k-1}$, we have that $u_{k+1}$ is the building edge of the region $\{A \cup B\}$. Hence, $u_{k+1}$ is a building edge for $\prec '$.

  Since $u_{k}$ is the edge of rank $k+1$ for the ordering $\prec '$, we may conclude that $\mathbf{B }'_{k+1} = \mathbf{B }'_{k}$ because the s and r belong to the same region $\{A \cup B\}$ of $\mathbf{B }'_{k}$. Therefore, $u_k$ is not a building edge for $\prec '$. This situation is illustrated in the following image.

  

  We conclude that ${\mathcal {B}}_\prec$ and ${\mathcal {B}}_{\prec '}$ have the same set of regions but not the same set of building edges: $E_{\prec '} = E_\prec {\setminus }\{u_{k}\} \cup \{u_{k+1}\}$. Hence, the only difference between the hierarchies ${\mathcal {B}}_\prec$ and ${\mathcal {B}}_{\prec '}$ is the building edge of the region $\{A \cup B\}$. Therefore, we may say that, if the weight of the building edge of $\{A \cup B\}$ for $\prec$ is equal to the weight of the building edge of $\{A \cup B\}$ for $\prec '$, then f is also one-side increasing for $\prec '$. To that end, we will prove that $f(u_k) = f(u_{k+1})$.

  By Lemma 22, as f is one-side increasing for $\prec$, we have that:

  • III. $(V,E_\prec )$ is a MST of (G, f)

  By the statement III and by Lemma 21, we conclude that:

  • IV. the hierarchy $\mathcal {QFZ}(G,f)$ is equal to the hierarchy $\mathcal {QFZ}((V,E_\prec ),f)$

  Statement IV implies that f is the saliency map of the hierarchy $\mathcal {QFZ}((V,E_\prec ),f)$. Hence, for any edge $u=\{a,b\}$ in E, f(u) is the maximum weight in the unique path between a and b in $((V,E_\prec ),f)$. We can affirm that:

  • V. the unique path between x and y in $((V,E_\prec ),f)$ is a path that includes the edge $u_{k}$

  By the statement V and by the definition of saliency maps, we have $f(u_{k+1}) \ge f(u_{k})$. Since k is a critical rank for f and $\prec$, we have $f(u_{k+1}) \le f(u_{k})$. Therefore, we have $f(u_k) = f(u_{k+1})$, which completes the proof that f is one-side increasing for $\prec '$.$\square$

Proof of Property 6

Property 6

Let $\prec$ be an altitude ordering for w and let $\epsilon$ be a map from the regions of ${\mathcal {B}}_{\prec }$ into $\mathbb {R}$. The map $\epsilon$ is an extinction map for $\prec$ if and only if the following statements hold true:

• $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\} = \{0, \ldots , n \}$;

• for any two distinct minima $M_1$ and $M_2$ of w, we have $\epsilon (M_1) \ne \epsilon (M_2)$; and

• for any region R of ${\mathcal {B}}_{\prec }$, we have that $\epsilon (R)$ is equal to $\vee \{\epsilon (M)$ such that M is a minimum of w included in $R\}$, where $\vee \{\}=0$.

We prove the forward and backward implications of Property 6 in Lemmas 35 and 36, respectively.

Lemma 35

Let $\prec$ be an altitude ordering for w and let $\epsilon$ be a map from the regions of ${\mathcal {B}}_{\prec }$ into $\mathbb {R}$. If the map $\epsilon$ is an extinction map for $\prec$, then the following statements hold true:

• 1. $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\} = \{0, \ldots , n \}$;

• 2. for any two distinct minima $M_1$ and $M_2$ of w, we have $\epsilon (M_1) \ne \epsilon (M_2)$; and

• 3. for any region R of ${\mathcal {B}}_{\prec }$, we have that $\epsilon (R)$ is equal to $\vee \{\epsilon (M)$ such that M is a minimum of w included in $R\}$, where $\vee \{\}=0$.

Proof

Let $\epsilon$ be an extinction map for $\prec$. Then, by the definition of extinction maps, there is a sequence ${\mathcal {S}}=(M_1, \ldots , M_n)$ of minima of w such that $\epsilon$ is the extinction map for $\prec$ and ${\mathcal {S}}$. We will prove that the statements 1, 2 and 3 hold true for $\epsilon$.

To prove that the statement 1 holds true, we will first prove that $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\} \subseteq \{0, \ldots , n \}$. Since w has n minima, the extinction value of any region of ${\mathcal {B}}_{\prec }$ which includes a minimum of w is in the set $\{1, \ldots , n\}$. On the other hand, for any region R of ${\mathcal {B}}_{\prec }$ which do not include any minimum of w, we have that $\epsilon (R) = 0$. Hence, $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\} \subseteq \{0, \ldots , n \}$. We will now prove that $\{0, \ldots , n \} \subseteq \{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\}$. As ${\mathcal {B}}_\prec$ has at least one leaf region composed of a single vertex of G, we can affirm that there is at least one region of ${\mathcal {B}}_\prec$ which do not include any minimum of w and whose extinction value for $\prec$ and ${\mathcal {S}}$ is zero. Then, 0 is in $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\}$. Now, let i be a value in $\{1, \ldots , n \}$. For the minimum $M_i$, we may affirm that $M_i$ is the unique minimum of w included in $M_i$ and, therefore, $\epsilon (M_i) = i$. Hence, i is in $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\}$. We may conclude that, for any i in $\{0, \ldots , n \}$, i is in $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\}$. Therefore, the range of $\epsilon$ is $\{0, \ldots , n\}$, which corresponds to the statement 1 of Lemma 35.

By the definition of extinction maps, for any minimum $M_i$, for i in $\{1, \ldots , n\}$, we have $\epsilon (M_i) = i$ because $M_i$ is the only minimum of w included in $M_i$. Therefore, for any two distinct minima $M_i$ and $M_j$, for i, j in $\{1, \ldots , n\}$, we have $\epsilon (M_i) = i$ and $\epsilon (M_j) = j$ and, consequently, $\epsilon (M_i)$ is different from $\epsilon (M_j)$. Hence, the statement 2 of Lemma 35 holds true for $\epsilon$.

The statement 3 of Lemma 35 is precisely the definition of extinction values: for any region R of ${\mathcal {B}}_{\prec }$, the extinction value of R is zero if there is no minimum of w included in R and, otherwise, it is the maximal i (which is equal to $\epsilon (M_i)$) such that $M_i$ is included in R. $\square$

Lemma 36

Let $\prec$ be an altitude ordering for w and let $\epsilon$ be a map from the regions of ${\mathcal {B}}_{\prec }$ into $\mathbb {R}$ such that:

• 1. $\{\epsilon (R) \mid R$ is a region of ${\mathcal {B}}_{\prec }\} = \{0, \ldots , n \}$;

• 2. for any two distinct minima $M_1$ and $M_2$ of w, we have $\epsilon (M_1) \ne \epsilon (M_2)$; and

• 3. for any region R of ${\mathcal {B}}_{\prec }$, we have that $\epsilon (R)$ is equal to $\vee \{\epsilon (M)$ such that M is a minimum of w included in $R\}$, where $\vee \{\}=0$.

Then, the map $\epsilon$ is an extinction map for $\prec$.

Proof

To prove that $\epsilon$ is an extinction map for $\prec$, we will show that there exists a sequence $S=(M_1, \ldots , M_n)$ of minima of w such that, for any region R of ${\mathcal {B}}_{\prec }$, the value $\epsilon (R)$ is the extinction value of R for $\prec$ and ${\mathcal {S}}$.

Let ${\mathcal {S}} = (M_1, \ldots , M_n)$ be a sequence of minima of w ordered in non-decreasing order for $\epsilon$, i.e. for any two distinct minima $M_i$ and $M_j$, with i, j in $\{1, \ldots , n\}$, if $\epsilon (M_i) <\epsilon (M_j)$ then $i < j$.

By the hypothesis 2, this sequence ${\mathcal {S}}$ is unique. By the hypothesis 3, for any region R of ${\mathcal {B}}$ such that there is no minimum of w included in R, $\epsilon (R) = \vee \{\} = 0$, so $\epsilon (R)$ is the extinction value of R for $\prec$ and ${\mathcal {S}}$.

Since w has n minima, for any minimum M of w, the value $\epsilon (M)$ is in $\{1, \ldots , n\}$. Otherwise, by contradiction, let us assume that there exists a minimum $M'$ of w such that $\epsilon (M') = 0$. Then, there is a value i in $\{1, \ldots , n\}$ such that, for any minimum $M''$ of w, the value $\epsilon (M'')$ is different from i. Consequently, by the hypothesis 3, the range of $\epsilon$ would be $\{0, \ldots , n\} {\setminus } \{i\}$, which contradicts the hypothesis 1. Therefore, for any minimum $M_i$ of w, for i in $\{1, \ldots , n\}$, as our assumption that $\epsilon (M_i) <\epsilon (M_j)$ implies that $i < j$, we have that $\epsilon (M_i) = i$. Thus, $\epsilon (M_i)$ is the extinction value of $M_i$ for $\prec$ and S.

It follows that, by the hypothesis 3, for any region R of ${\mathcal {B}}_{\prec }$ such that there is a minimum of w included in R, the value $\epsilon (R)$ is the maximum value i (which is equal to $\epsilon (M_i)$) in $\{1, \ldots , n\}$ such that $M_i$ is included in R.

Thus, for any region R of ${\mathcal {B}}_{\prec }$, the value $\epsilon (R)$ is the extinction value of R for $\prec$ and ${\mathcal {S}}$. Therefore, the map $\epsilon$ is an extinction map for $\prec$. $\square$

Proof of Lemma 11

Lemma 11

Let $\prec$ be an altitude ordering for w, let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$, and let $\xi$ be the approximated extinction map for f and $\prec$. The map $\xi$ is an extinction map for $\prec$.

In order to prove Lemma 11, we prove in Lemmas 38, 39 and 43 that the three conditions of Property 6 for $\xi$ to be an extinction map are satisfied. We first establish the following auxiliary lemma.

Lemma 37

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Then, the two following statements hold true:

• 1. the set $\{f(e) \mid e\ is\ a\ watershed-cut\ edge\ for\ \prec \}$ is equal to $\{1, \ldots , n-1\}$; and

• 2. for any two distinct watershed-cut edges u and v for ${\mathcal {B}}$, we have $f(u) \ne f(v)$.

Proof

By Definition 3 (statement 1), we have $\{f(u) \mid u \in E_\prec \}=\{0, \ldots , n-1\}$ and, by Definition 3 (statement 2), only the weight of the watershed-cut edges for $\prec$ are strictly greater than zero. Then, $\{f(e) \mid e\ is\ a\ watershed-cut\ edge\ for\ \prec \} = \{1, \ldots , n-1\}$. Hence, for any i in $\{1, \ldots , n-1\}$, there is a watershed-cut edge e for $\prec$ such that $f(e) = i$. Moreover, as there are $n-1$ watershed-cut edges for $\prec$, for any two distinct watershed-cut edges u and v for $\prec$, we have $f(u) \ne f(v)$. $\square$

Lemma 38

Let $\prec$ be an altitude ordering for w, let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$, and let $\xi$ be the approximated extinction map for f and $\prec$. The range of $\xi$ is $\{0,\ldots ,n\}$.

Proof

We will prove that: (1) for any i in $\{0, \ldots , n\}$, there is a region R of ${\mathcal {B}}_{\prec }$ such that $\xi (R) = i$; and (2) for any region R of ${\mathcal {B}}_{\prec }$, we have $\xi (R)$ in $\{0, \ldots , n\}$.

• (1) We first prove statement (1). We start by proving that there is a region R of ${\mathcal {B}}_{\prec }$ such that $\xi (R) = n$. Let R be the set V of vertices of G. Then, by Definition 10 (statement 1), we have $\xi (R) = \bigtriangledown (R)+1$, where $\bigtriangledown$ is the supremum descendant map for f and $\prec$. By Definition 3 (statement 1), we have $\{f(u) \mid u \in E_\prec \}=\{0, \ldots , n-1\}$. As $\bigtriangledown (V) = \vee \{f(u) \mid R_u \subseteq V\} = \vee \{0, \ldots , n-1\}= n-1$, we have that $\xi (R) = n-1+1 = n$.

  We will now show that there is a region R of ${\mathcal {B}}_{\prec }$ such that $\xi (R) = 0$. Let R be a region of ${\mathcal {B}}_\prec$ such that there is no minimum of w included in R. Then, R is not a minimum of w and, consequently, the building edge of the parent of R is not a watershed-cut edge for $\prec$. Let u be building edge of the parent of R. Since there is no minimum of w included in R, by Definition 9, R is not a dominant region for f and $\prec$. By the statement 3 of the definition of approximated extinction maps (Definition 10), we have $\xi (R)=f(u)$. Since f is a one-side increasing map and since u is not a watershed-cut edge for $\prec$, we have $f(u) = 0$. Therefore, we have $\xi (R) = f(u) = 0$.

  Finally, we will prove that, for any i in $\{1, \ldots , n-1\}$, there is a region R of ${\mathcal {B}}_\prec$ such that $\xi (R) = i$. By Lemma 37, we can say that, for any i in $\{1, \ldots , n-1\}$, there is a watershed-cut u edge for $\prec$ such that $f(u)=i$. Let u be a watershed-cut edge for $\prec$ and let X and Y be the children of $R_u$. Since u is a watershed-cut edge for $\prec$, both X and Y contain at least a minimum of w and, then, neither X nor Y are leaf regions of ${\mathcal {B}}_\prec$. Let $\ll$ be the non-leaf ordering for f and $\prec$. Since $\ll$ is a total ordering, we have either $X \ll Y$ or $Y \ll X$. Then, exactly one child of $R_u$ is a dominant region for f and $\prec$. Let Y (resp. X) be the child of $R_u$ which is not a dominant region for f and $\prec$. By Definition 10 (statement 3), we have $\xi (Y) = f(u)$ (resp. $\xi (X) = f(u)$). Therefore, for any i in $\{1, \ldots , n-1\}$, there is a watershed-cut edge u for $\prec$ such that $f(u) = i$ and such that there is a child Z of $R_u$ such that $\xi (Z) = i$.

• (2) We will now prove the statement 2. Let R be a region of ${\mathcal {B}}_{\prec }$. If $R= V$, then $\xi (R) = n$, as established in the proof of statement 1. Otherwise, let v be the building edge of the parent of R. By Definition 10, the value $\xi _f(R)$ is either f(v) or $\xi (parent(R))$. Hence, either $\xi _f(R)$ is equal to f(v) for a building edge v for $\prec$, or $\xi _f(R)$ is equal to $\xi (V) = n$. It is enough to prove that n and f(v) are in $\{0, \ldots , n\}$. As f is one-side increasing for $\prec$, by Definition 3 (statement 1), we have $\{f(u) \mid u \in E_\prec \} = \{0, \ldots , n-1\}$. Since v is a building edge for $\prec$, we may say that f(v) is in $\{0, \ldots , n-1\}$.$\square$

Lemma 39

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Let $\xi$ be the approximated extinction map for f and $\prec$. For any two minima $M_1$ and $M_2$ of w, if $\xi (M_1) = \xi (M_2)$, then $M_1 = M_2$.

To prove Lemma 39, we first present the Lemmas 40, 41 and 42 . In the following, for any non-leaf region X of a binary partition hierarchy ${\mathcal {B}}$ of (G, w), we denote by $u_X$ the building edge of X.

Lemma 40

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Let $\xi$ be the approximated extinction map for f and $\prec$. For any region X of ${\mathcal {B}}_{\prec }$ such that there is a minimum M of w such that $M \subset X$, there is a child Y of X such that:

• 1. $\xi (Y) = \xi (X)$;

• 2. $\xi (sibling(Y)) = f(u_X)$; and

• 3. there is a minimum of w included in Y.

Proof

Let X be a region such that there is a minimum M of w such that $M \subset X$. Then, there is a child Z of X such that there is a minimum M such that $M \subseteq Z$. Let Z be a child X such that there is a minimum M such that $M \subseteq Z$. We consider two cases: (1) sibling(Z) is a leaf region of ${\mathcal {B}}_\prec$; and (2) sibling(Z) is a non-leaf region of ${\mathcal {B}}_\prec$.

• (1) If sibling(Z) is a leaf region of ${\mathcal {B}}_\prec$, then, by Definition 9, Z is a dominant region for f and $\prec$ and sibling(Z) is not a dominant region for f and $\prec$. Hence, by Definition 10, $\xi (Z) = \xi (X)$ and $\xi (sibling(Z)) = f(u_X)$.

• (2) Let us now assume that sibling(Z) is a non-leaf region of ${\mathcal {B}}_\prec$. Since X is not a minimum of w and since there is a minimum of w included in Z, we can conclude that there is a minimum of w included in sibling(Z) as well. Let $\ll$ be the non-leaf ordering for f and $\prec$. As the non-leaf ordering $\ll$ is a total ordering on the non-leaf regions of ${\mathcal {B}}_\prec$, we have either $Z \ll sibling(Z)$ or $sibling(Z) \ll Z$. Then, by the definition of dominant regions (Definition 9), we have that either Z or sibling(Z) is a dominant region for f and $\prec$. Let us assume that Z is a dominant region for f and $\prec$. Then, by Definition 10, we have $\xi (Z) = \xi (X)$ and $\xi (sibling(Z)) = f(u_X)$. Otherwise, if sibling(Z) is a dominant region for f and $\prec$, we have $\xi (sibling(Z)) = \xi (X)$ and $\xi (Z) = f(u_X)$. Since both Z and sibling(Z) include at least one minimum of w, we may say that there is a child Y of X for which the hypothesis 1, 2 and 3 hold true.$\square$

Lemma 41

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Let $\xi$ be the approximated extinction map for f and $\prec$. Let u be a watershed-cut edge for $\prec$. Then, there is a minimum M of w such that $\xi (M) = f(u)$.

Proof

As u is a watershed-cut edge for $\prec$, each child of $R_u$ includes at least one minimum of w. Then, there is a minimum M of w such that $M \subset R_u$. By Lemma 40, there is a child $Y_1$ of $R_u$ such that $\xi (Y_1) = f(u)$. If $Y_1$ is a minimum of w, then the property holds true. Otherwise, if $Y_1$ is not a minimum of w, it means that there is a minimum M of w such that $M \subset Y_1$. By Lemma 40, there is a child $Y_2$ of $Y_1$ such that $\xi (Y_2) = \xi (Y_1) = f(u)$ and such that there is a minimum of w included in $Y_2$. Again, if $Y_2$ is a minimum of w, then the property holds true. Otherwise, we can apply this same reasoning indefinitely. We can define a sequence $(Y_1, \ldots , Y_p)$ of regions of ${\mathcal {B}}_\prec$ where $Y_p$ is a minimum of w and such that $\xi (Y_p) = \ldots = \xi (Y_1) = f(u)$ and $Y_i \subset Y_{i-1}$ for any i in $\{2, \ldots , p\}$. Therefore, there is a minimum $Y_p$ included in $R_u$ such that $\xi (Y_p) = f(u)$. $\square$

Lemma 42

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Let $\xi$ be the approximated extinction map for f and $\prec$. Let X be a region of ${\mathcal {B}}_\prec$ such that X contains at least one minimum of w. There exists a minimum $M \subseteq X$ such that $\xi (M) = \xi (X)$.

Proof

If X is a minimum of w, then it is trivial. Otherwise, by Lemma 40, there is a child $Y_1$ of X such that $\xi (Y_1) = \xi (X)$ and such that there is a minimum of w included in $Y_1$. If $Y_1$ is a minimum of w, then the property holds true. Otherwise, by Lemma 40, there is a child $Y_2$ of $Y_1$ such that $\xi (Y_2) = \xi (Y_1) = \xi (X)$ and such that there is a minimum of w included in $Y_2$. Again, if $Y_2$ is a minimum of w, then the property holds true. Otherwise, we can apply this same reasoning indefinitely. We can define a sequence $(Y_1, \ldots , Y_p)$ of regions of ${\mathcal {B}}_\prec$ where $Y_p$ is a minimum of w and such that $\xi (Y_p) = \ldots = \xi (Y_1) = \xi (X)$ and $Y_i \subset Y_{i-1}$ for any i in $\{2, \ldots , p\}$. Therefore, there is a minimum $Y_p$ included in X such that $\xi (Y_p) = \xi (Y)$. $\square$

Proof of Lemma 39

In order to prove that

• (1) for any two minima $M_1$ and $M_2$ of w, if $\xi (M_1) = \xi (M_2)$, then $M_1 = M_2$,

we will prove that

• (2) for any two minima $M_1$ and $M_2$ of w, we have $\xi (M_1) \ne \xi (M_2)$.

As w has n minima, it suffices to prove that, for any i in $\{1, \ldots , n\}$, there is a minimum M of w such that $\xi (M)=i$.

By Lemma 41, for any watershed-cut edge u for ${\mathcal {B}}_{\prec }$, there is a minimum M such that $\xi (M) = f(u)$. By Lemma 37, for any i in $\{1, \ldots , n-1\}$, there is a watershed-cut edge such that $f(u)=i$. Then, for any i in $\{1,\ldots , n-1\}$, there is a minimum M of w such that $\xi (M)=i$.

Since, f is one-side increasing for $\prec$, we have $\vee \{f(v) \mid R_v \in V\} = \{0,\ldots ,n-1\}$. Then, we can conclude that $\xi (V) = \vee \{f(v) \mid R_v \in V\} + 1 = (n-1)+1= n$. By Lemma 42, there is a minimum M of w such that $\xi (M) = \xi (V) = n$.

Therefore, for any i in $\{1,\ldots , n\}$, there is a minimum M of w such that $\xi (M)=i$. Since w has n minima, it implies that the values $\xi (M_1)$ and $\xi (M_2)$ are distinct for any pair $(M_1, M_2)$ of distinct minima of w. Hence, for any two minima $M_1$ and $M_2$ of w, if $\xi (M_1) = \xi (M_2)$, then $M_1 = M_2$. $\square$

Lemma 43

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Let $\xi$ be the approximated extinction map for f and $\prec$. For any region R of ${\mathcal {B}}_\prec$, we have $\xi _f(R) = \vee \{\xi _f(M)$ such that M is a minimum of w included in $R\}$.

To prove Lemma 43, we introduce Lemma 44.

Lemma 44

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Let $\xi$ be the approximated extinction map for f and $\prec$. Let $\bigtriangledown$ be the supremum descendant map for f and $\prec$. Let X be a region of ${\mathcal {B}}_\prec$. Then, $\xi (X)$ is greater than or equal to the supremum descendant value $\bigtriangledown (X)$ of X.

Proof

We consider the following cases: (1) $X=V$, (2) $X \ne V$ and X is not a dominant region for f and $\prec$; and (3) X is a dominant region for f and $\prec$. Let $\ll$ be the non-leaf ordering for f and $\prec$.

• 1. If $X = V$, then $\xi (X) = \xi (V) = \bigtriangledown (V)+1$ (first case of Definition 10). Then, $\xi (X)$ is clearly than $\bigtriangledown (X)$.

• 2. If $X\ne V$ and if X is not a dominant region for f and $\prec$, then $\xi (X) = f(u)$ (third case of Definition 10), where u is the building edge of the parent of X. By the definition of dominant regions, we consider two cases: (a) there is no minimum M of w such that $M \subseteq X$; or (b) $X \ll sibling(X)$.

  • (a) If there is no minimum M of w such that $M \subseteq X$, then there is no descendant of X whose building edge is a watershed-cut edge for $\prec$. Hence, for any edge v such that $R_v \subseteq X$, u is not a watershed-cut edge for $\prec$ and, since f is one-side increasing for $\prec$, we have $f(v)=0$ Definition 3 (statement 2). Therefore, $\bigtriangledown (X)=0$. By Definition 3 (statement 1), we have $\{f(v) \mid v \in E_\prec \}=\{0, \ldots , n-1\}$. Hence, $\xi (X)$, being equal to f(u), is greater than or equal to $\bigtriangledown (X)=0$.

  • (b) If $X \ll sibling(X)$, then, by the definition of non-leaf ordering, we have:

    • (i) either $\bigtriangledown (X) < \bigtriangledown (sibling(X))$; or

    • (ii) $\bigtriangledown (X) = \bigtriangledown (sibling(X))$ and $u_X \prec u_{sibling(X)}$.

    Thus, we have $\bigtriangledown (X) \le \bigtriangledown (sibling(X))$. Since f is one-side increasing for $\prec$, by the statement 3 of Definition 3, there is a child Y of parent(X) such that $f(u) \ge \vee \{f(v) \mid R_v \subseteq Y\}$. Hence, there is a child Y of parent(X) such that $f(u) \ge \bigtriangledown (Y)$. Then, we have $f(u) \ge \bigtriangledown (X)$ or $f(u) \ge \bigtriangledown (sibling(X))$. In the case where $f(u) \ge \bigtriangledown (sibling(X))$, this also implies that $f(u) \ge \bigtriangledown (X)$ because $\bigtriangledown (X) \le \bigtriangledown (sibling(X))$. Therefore, $\xi (X)$, being equal to f(u), is greater than or equal to $\bigtriangledown (X)$.

• 3. If X is a dominant region for f and $\prec$, then $\xi (X) = \xi (parent(X))$ (second case of Definition 10). We will prove by induction that this lemma holds true for any dominant region for f and $\prec$. In the base step, we consider that parent(X) is V. In the inductive step, we show that, if the property holds true for parent(X), then it also holds true for X. Please note that, if parent(X) is not a dominant region for f and $\prec$, the property holds for parent(X) as proven in the previous case.

  • (a) Base step: if parent(X) is V, then $\xi (X) = \xi (V) = \bigtriangledown (V)+1$ (first case of Definition 10). We can see that $\bigtriangledown (V) \ge \bigtriangledown (X)$ because, for any edge u such that $R_u \subseteq X$, we also have $R_u \subseteq V$. Then, $\xi (X)$, being equal to $\bigtriangledown (V)+1$, is greater than $\bigtriangledown (X)$.

  • (b) Inductive step: let us assume that $\xi (parent(X)) \ge \bigtriangledown (parent(X))$. Since $\xi (X) = \xi (parent(X))$, we have $\xi (X) \ge \bigtriangledown (parent(X))$. We can affirm that, for any edge v in $E_\prec$ such that $R_v \subseteq X$, we also have $R_v \subseteq parent(X)$. Hence, $\bigtriangledown (parent(X)) \ge \bigtriangledown (X)$. Therefore, $\xi (X)$, being equal to $\xi (parent(X))$, is greater than or equal to $\bigtriangledown (X)$. $\square$

Proof of Lemma 43

We will prove that, for any region X of ${\mathcal {B}}_\prec$, we have $\xi (X) = \vee \{\xi _f(M)$ such that M is a minimum of w included in $X\}$. Let X be a region of ${\mathcal {B}}_\prec$. We consider two cases: (1) there is a minimum of w included in X; and (2) there is no minimum of w included in X.

• (1) If there is no minimum of w included in X, then X is not a dominant region for f and $\prec$. Then, $\xi (X) = f(u)$ (third condition of Definition 10), where u is the building edge of parent(X). The edge u is not a watershed-cut edge for $\prec$ because the child X of $R_u$ does not include any minimum of w. Hence, since f is one-side increasing for $\prec$, by the statement 2 of Definition 3, we have $f(u)=0$. Therefore, $\xi (X)$, being equal to f(u), is also equal to $\vee \{\xi (M)$ such that M is a minimum of w included in $R\} = \vee \{\} = 0$.

• (2) Let us assume that there is at least one minimum of w included in X. If X is a minimum of w, then $\xi (X) = \vee \{\xi _f(M)$ such that M is a minimum of w included in $X\}=\vee \{\xi _f(X)\}$.

  In order to prove the case where X is not a minimum of w, we will first demonstrate that $\xi (X) \ge \vee \{\xi (Y) \mid Y \subseteq X\}$.

  To prove that $\xi (X) \ge \vee \{\xi (Y) \mid Y \subseteq X\}$, it is enough to demonstrate that, for any region Z of ${\mathcal {B}}_\prec$, we have $\xi (Z) \ge \vee \{\xi (Y) \mid Y\ is\ a\ child\ of\ Z\}$. Let Z be a region of ${\mathcal {B}}_\prec$. If Z is a leaf region of ${\mathcal {B}}_\prec$, then $\xi (Z) \ge \vee \{\xi (Y) \mid Y\ is\ a\ child\ of\ Z\}=\vee \{\}=0$ because, by Lemma 38, $\xi (Z)$ is in $\{0, \ldots , n\}$. Let us now assume that Z is not a leaf region of ${\mathcal {B}}_\prec$ and let Y be a child of Z. If Y is a dominant region for f and $\prec$, then $\xi (Y)=\xi (Z)$ and, consequently, $\xi (Z) \ge \xi (Y)$. Otherwise, if Y is not a dominant region for f and $\prec$, then $\xi (Y)=f(v)$, where v is the building edge of Z. By Lemma 44, $\xi (Z) \ge \bigtriangledown (Z)$ and, consequently, $\xi (Z) \ge f(u)$. Hence, $\xi (Z) \ge \xi (Y)$.

  We can now prove that $\xi (X) = \vee \{\xi _f(M)$ such that M is a minimum of w included in $X\}$ in the case where X is not a minimum of w. By Lemma 42, there is a minimum M of w such that $M \subset X$ and such that $\xi (M) = \xi (X)$. Let M be the minimum of w such that $\xi (M) = \xi (X)$. Since $\xi (X) \ge \vee \{\xi (Y) \mid Y \subseteq X\}$, we can say that $\xi (X) = \vee \{\xi _f(M')$ such that $M'$ is a minimum of w included in $X\}$.$\square$

Proof of Lemma 12

Lemma 12

Let $\prec$ be an altitude ordering for w and let f be a map from E into $\mathbb {R}$ such that f is one-side increasing for ${\mathcal {B}}_{\prec }$. Then, for any u in $E_\prec$, we have:

$$\begin{aligned} f(u) = min\{\xi (R) \text { such that } R \text { is a child of } R_u\}. \end{aligned}$$

Proof

Let u be an edge in $E_\prec$. By the definition of dominant regions, we have that at most one child of $R_u$ is a dominant region for f and $\prec$. Therefore, there is a child of $R_u$ which is not a dominant region for f and $\prec$. Let X be the child of $R_u$ which is not a dominant region for f and $\prec$. Then, $\xi (X) = f(u)$ (by the third condition of Definition 10). If sibling(X) is not a dominant region for f and $\prec$, then $\xi (sibling(X)) = f(u)$ as well and, consequently, $f(u) = min\{\xi (R)$ such that R is a child of $R_u\}= min\{f(u),f(u)\}$. Otherwise, let us assume that sibling(X) is a dominant region for f and $\prec$. Then, $\xi (sibling(X)) = \xi (R_u)$. By Lemma 44, we can infer that $\xi (R_u) \ge f(u)$. Therefore, $min\{\xi (Y)$ such that Y is a child of $R_u\} = min\{\xi _f(X), \xi (sibling(X))\} = min\{f(u), \xi (R_u)\} = f(u)$. $\square$

Proof of Lemma 4

Lemma 4

Let ${\mathcal {H}}$ be a hierarchy on V. The hierarchy ${\mathcal {H}}$ is a hierarchical watershed of (G, w) if and only if there is an altitude ordering $\prec$ for w such that $\varPhi ({\mathcal {H}})$ is one-side increasing for $\prec$.

Proof

We prove the forward and backward implications of Lemma 4 in Lemmas 45 and 46, respectively. $\square$

Lemma 45

Let ${\mathcal {H}}$ be a hierarchy on V. If the hierarchy ${\mathcal {H}}$ is a hierarchical watershed of (G, w), then there exists an altitude ordering $\prec$ for w such that $\varPhi ({\mathcal {H}})$ is one-side increasing for $\prec$.

Proof

By Lemma 16, there is a sequence of minima ${\mathcal {S}}$ of w such that ${\mathcal {H}}$ is the hierarchy induced by $\prec$ and ${\mathcal {S}}$. In order to prove that $\varPhi ({\mathcal {H}})$ is one-side increasing for $\prec$, by Definition 3, we will prove that the following three statements hold true:

• 1. $\{\varPhi ({\mathcal {H}})(e) \mid e \in E_\prec \} = \{0, \ldots , n-1\}$;

• 3. for any edge u in $E_\prec$, $\varPhi ({\mathcal {H}})(u) > 0$ if and only if u is a watershed-cut edge for $\prec$; and

• 4. for any edge u in $E_\prec$, there exists a child R of $R_u$ such that $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $R\}$, where $\vee \{\} = 0$.

In the remainder of this proof, let $\rho$ and $\epsilon$ be, respectively, the persistence map and the extinction map for $\prec$ and ${\mathcal {S}}$.

• 1. By Lemma 20, we have $\{\varPhi ({\mathcal {H}})(e) \mid e \in E_\prec \} = \{\rho (e) \mid e \in E_\prec \}$. Then, as Lemma 19 states that the range of $\rho$ is $\{0, \ldots , n-1\}$, we can conclude that $\{\varPhi ({\mathcal {H}})(e) \mid e \in E_\prec \}$ is the set $\{0, \ldots , n-1\}$.

• 2. Let u be a building edge for $\prec$. Given the following propositions:

  • (a) u is a watershed-cut edge

  • (b) $\varPhi ({\mathcal {H}})(u) > 0$

  we will prove that (a) implies (b), and that not (b) implies not (a).

  If u is a watershed-cut edge for $\prec$, then both children of $R_u$ contain at least one minimum of w. Therefore, the extinction value of both children of $R_u$ is nonzero and, consequently, the persistence value $\rho (u)$ of u is nonzero. Moreover, by Lemma 20, in this case we have $\varPhi ({\mathcal {H}})(e)=\rho (e)$ for any building edge e for $\prec$. Thus, $\varPhi ({\mathcal {H}})(u)$ is nonzero.

  On the other hand, if u is not a watershed-cut edge for $\prec$, then there is a child X of $R_u$ which does not contain any minimum of w. Therefore, the extinction value of X is equal to 0: $\epsilon (X)=0$. Since, by definition $\rho (u) = min\{\epsilon (X), \epsilon (sibling(X))\}$ and the minimal extinction value is zero, we can say that $\rho (u) = 0$. Again, by Lemma 20, in this case we have $\varPhi ({\mathcal {H}})(e)=\rho (e)$ for any building edge e for $\prec$ and thus, $\varPhi ({\mathcal {H}})(u)$ is equal to 0.

• 3. Let u be a building edge for $\prec$. The persistence value of u is the extinction value of a child X of $R_u$. Let X be a child of $R_u$ such that $\rho (u)$, the persistence value of u, is equal to $\epsilon (X)$, the extinction value of X. By Lemma 17, for any region Y of ${\mathcal {B}}_\prec$ such that $Y \subseteq X$ , we have $\epsilon (Y) \le \epsilon (X)$ and, as $X\subseteq R_u$, $\epsilon (Y) \le \epsilon (R_u)$. Let v be the building edge of a region $Z \subseteq X$. Then, we can say that the extinction value of both children of Z is less than or equal to the extinction value $\epsilon (X)$. Hence, $\rho (v) \le \epsilon (X)$ and, then, $\rho (v) \le \rho (u)$. By Lemma 20, we can conclude that $\varPhi ({\mathcal {H}})(v) \le \varPhi ({\mathcal {H}})(u)$. Hence, $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $X\}$. $\square$

Lemma 46

Let ${\mathcal {H}}$ be a hierarchy on V and let $\prec$ be an altitude ordering such that $\varPhi ({\mathcal {H}})$ is one-side increasing for $\prec$. Then, the hierarchy ${\mathcal {H}}$ is a hierarchical watershed of (G, w).

Proof

Let $\xi$ be the approximated extinction map for $\varPhi ({\mathcal {H}})$ and $\prec$. By Lemma 12, for any edge in $E_\prec$, we have  $\varPhi ({\mathcal {H}})(u) = min\{\xi (R)$ such that R is a child of $R_u\}$. By Lemma 11, the map $\xi$ is an extinction map for $\prec$. Then, by the backward implication of Property 7, the hierarchy ${\mathcal {H}}$ is a hierarchical watershed of (G, w). $\square$

Proof of Property 14

Property 14

Let ${\mathcal {H}}$ be a hierarchy on V. The hierarchy ${\mathcal {H}}$ is a flattened hierarchical watershed of (G, w) if and only if there is an altitude ordering $\prec$ for w such that:

• 1. $(V, E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$; and

• 2. for any edge u in $E_\prec$, if u is not a watershed-cut edge for $\prec$, then $\varPhi ({\mathcal {H}})(u) = 0$; and

• 3. for any edge u in $E_\prec$, there exists a child R of $R_u$ such that $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $R\}$, where $\vee \{\} = 0$.

To prove Property 14, we establish the following lemma.

Lemma 47

Let $\prec$ be an altitude ordering for w and let ${\mathcal {H}}$ be a hierarchy on V such that $\varPhi ({\mathcal {H}})$ is one-side increasing for $\prec$. Then, $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$.

Proof

Let $\alpha$ denote the sum of the weight of the edges in $E_\prec$ in the map $\varPhi ({\mathcal {H}})$: $\alpha = \sum _{e\in E_\prec }\varPhi ({\mathcal {H}})(e)$. As $\varPhi ({\mathcal {H}})$ is one-side increasing for $\prec$, by the condition 1 of Definition 3, we can affirm that $\alpha = 0 + 1 + \ldots + n-1$. In order to prove that $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$, we will prove that, for any MST $G'$ of $(G,\varPhi ({\mathcal {H}}))$, the sum of the weight of the edges in $G'$ is greater than or equal to $\alpha$. Let $G'$ be a MST of $(G, \varPhi ({\mathcal {H}}))$. As $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}))$, by the condition 1 of Lemma 21, we have that G and $G'$ have the same quasi-flat zones hierarchy: $\mathcal {QFZ}(G, \varPhi ({\mathcal {H}}))= \mathcal {QFZ}(G', \varPhi ({\mathcal {H}}))$. As $\varPhi ({\mathcal {H}})$ is the saliency map of ${\mathcal {H}}$, we have that ${\mathcal {H}} = \mathcal {QFZ}(G, \varPhi ({\mathcal {H}}))$. Therefore, ${\mathcal {H}} = \mathcal {QFZ}(G', \varPhi ({\mathcal {H}}))$. Let i be a value in $\{1, \ldots , n-1\}$. By the condition 1 of Definition 3, we can say that $\{1, \ldots , n-1\}$ is a subset of the range of $\varPhi ({\mathcal {H}})$. Therefore, ${\mathcal {H}}$ is composed of at least n distinct partitions. Let ${\mathcal {H}}$ be the sequence $(\mathbf{P }_0, \ldots , \mathbf{P }_{n-1}, \ldots )$. Since the partitions $\mathbf{P }_{i}$ and $\mathbf{P }_{i-1}$ are distinct, then there exists a region in $\mathbf{P }_i$ which is not in $\mathbf{P }_{i-1}$. Therefore, there is a region X of $\mathbf{P }_i$ which is composed of a several regions $\{R_1, R_2, \ldots \}$ of $\mathbf{P }_{i-1}$. Then, there are two adjacent vertices x and y such that x and y are in distinct regions in $\{R_1, R_2, \ldots \}$. Let x and y be two adjacent vertices such that x and y are in distinct regions in $\{R_1, R_2, \ldots \}$. Hence, the lowest j such that x and y belong to the same region of $\mathbf{P }_j$ is i. Thus, there exists an edge $u=\{x,y\}$ in $E_\prec$ such that $\varPhi ({\mathcal {H}})(u)=i$. Hence, the sum of the weight of the edges of $G'$ is at least $1 + \ldots + n-1$, which is equal to $\alpha$. Therefore, the graph $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$. $\square$

The reader can observe that the statement 3 of the above property is precisely the statement 3 of the definition of one-side increasing maps (Definition 3), and that the statement 2 is an implication of the statement 2 of Definition 3. The statement 1 of the above property corresponds to a property of one-side increasing maps established in Lemma 47.

In order to prove Property 14, we establish some auxiliary lemmas on MSTs and saliency maps.

In the following, we state a well-known property of spanning trees in Lemma 48.

Let x and y be two vertices in V and let $\pi =(x_0,\ldots ,x_p)$ be a path from x to y. For any edge $u=\{x_{i-1}, x_i\}$ for i in $\{1, \ldots , p\}$, we say that uis in$\pi$ or that $\pi$includesu.

Lemma 48

Let $G'$ be a spanning tree of a weighted graph (G, f). Let $u=\{x,y\}$ be an edge in $E {\setminus } E(G')$ and let $\pi$ be the path from x to y (resp. y to x) in $G'$. The graph $G'$ is a MST of (G, f) if and only if $f(u) \ge f(v)$ for any edge v in $\pi$.

The following lemma characterizes MSTs of saliency maps.

Lemma 49

Let f be the saliency map of a hierarchy on V and let $G'$ be a spanning tree of (G, f). Let $u=\{x,y\}$ be an edge in $E {\setminus } E(G')$ and let $\pi$ be the path from x to y (resp. y to x) in $G'$. Let v be an edge of greatest weight in $\pi$. The graph $G'$ is a MST of (G, f) if and only if $f(u) = f(v)$.

Proof

We will first prove the forward implication of this lemma. Let $G'$ be a MST of $(G,\varPhi ({\mathcal {H}}))$. Then, by Lemma 48, for any edge e in the path $\pi$, we have $\varPhi ({\mathcal {H}})(e) \le \varPhi ({\mathcal {H}}(u)$. Hence, $\varPhi ({\mathcal {H}})(v) \le \varPhi ({\mathcal {H}}(u)$. Let us assume that $\varPhi ({\mathcal {H}})(v) < \varPhi ({\mathcal {H}})(u)$. Then, given $\lambda =\varPhi ({\mathcal {H}})(v)$, in the $\lambda$-level set of $(G,\varPhi ({\mathcal {H}}))$, the vertices x and y are connected, which implies that, by the definition of saliency maps, $\varPhi ({\mathcal {H}}(u)$ is less or equal to $\varPhi ({\mathcal {H}})(v)$, which contradicts our assumption. Hence, $\varPhi ({\mathcal {H}})(v) = \varPhi ({\mathcal {H}}(u)$.

Now, let us assume that $\varPhi ({\mathcal {H}})(u)$ is equal to the greatest weight among the edges in $\pi$. Then, for any edge e in the path $\pi$, we have $\varPhi ({\mathcal {H}})(e) \le \varPhi ({\mathcal {H}}(u)$. Then, by Lemma 48, $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}))$. $\square$

Lemma 50

Let ${\mathcal {H}}'$ be a hierarchy on V and let ${\mathcal {H}}$ be a flattening of ${\mathcal {H}}'$. Let u and v be two distinct edges in E such that $\varPhi ({\mathcal {H}})(u) < \varPhi ({\mathcal {H}})(v)$. Then, $\varPhi ({\mathcal {H}}')(u) < \varPhi ({\mathcal {H}}')(v)$.

Proof

Let $u = \{x_1,y_1\}$ and $v = \{x_2,y_2\}$. As $\varPhi ({\mathcal {H}})(u) < \varPhi ({\mathcal {H}})(v)$, there is a partition $\mathbf{P }$ of ${\mathcal {H}}$ such that $x_1$ and $y_1$ belong to the same region of $\mathbf{P }$ and we such that $x_2$ and $y_2$ do not belong to the same region of $\mathbf{P }$. As $\mathbf{P }$ is a partition of ${\mathcal {H}}'$, there is a partition in ${\mathcal {H}}'$ such that $x_1$ and $y_1$ belong to the same region of this partition but $x_2$ and $y_2$ do not. Then, $\varPhi ({\mathcal {H}}')(u) < \varPhi ({\mathcal {H}}')(v)$. $\square$

Lemma 51

Let ${\mathcal {H}}'$ be a hierarchy on V and let ${\mathcal {H}}$ be a flattening of ${\mathcal {H}}'$. Let u and v be two distinct edges in E such that $\varPhi ({\mathcal {H}}')(u) \le \varPhi ({\mathcal {H}}')(v)$. Then, $\varPhi ({\mathcal {H}})(u) \le \varPhi ({\mathcal {H}})(v)$.

Proof

Let $u = \{x_1,y_1\}$ and $v = \{x_2,y_2\}$. As $\varPhi ({\mathcal {H}}')(u) \le \varPhi ({\mathcal {H}}')(v)$, then for any partition $\mathbf{P }$ of ${\mathcal {H}}'$, if $x_2$ and $y_2$ are in the same region of $\mathbf{P }$, then $x_1$ and $y_1$ are in the same region of $\mathbf{P }$ as well. As any partition of ${\mathcal {H}}$ is also a partition of ${\mathcal {H}}'$, we may say that for any partition $\mathbf{P }$ of ${\mathcal {H}}$, if $x_2$ and $y_2$ are in the same region of $\mathbf{P }$, then $x_1$ and $y_1$ are in the same region of $\mathbf{P }$. Hence, $\varPhi ({\mathcal {H}})(u) \le \varPhi ({\mathcal {H}})(v)$. $\square$

The forward and backward implications of Property 14 are proven in Lemmas 52 and 53, respectively.

Lemma 52

Let ${\mathcal {H}}$ be a flattened hierarchical watershed of (G, w). Then, there is an altitude ordering $\prec$ for w such that:

• 1. $(V, E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$; and

• 2. for any building edge u for $\prec$, if u is not a watershed-cut edge for $\prec$, then $\varPhi ({\mathcal {H}})(u) = 0$; and

• 3. for any building edge u for $\prec$, there exists a child R of $R_u$ such that $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $R\}$, where $\vee \{\} = 0$.

Proof

As ${\mathcal {H}}$ is a flattened hierarchical watershed of (G, w), by Definition 13, there is a hierarchical watershed ${\mathcal {H}}_w$ of (G, w) such that ${\mathcal {H}}$ is a flattening of ${\mathcal {H}}_w$. By Lemma 4, there is an altitude ordering $\prec$ for w such that $\varPhi ({\mathcal {H}}_w)$ is one-side increasing for $\prec$. Let $\prec$ be the altitude ordering for w such that $\varPhi ({\mathcal {H}}_w)$ is one-side increasing for $\prec$. By Lemma 22, $(V,E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}_w))$. Let $G'$ denote the graph $(V, E_\prec )$. By Lemma 21, ${\mathcal {H}}_w$ is the hierarchy $\mathcal {QFZ}(G', \varPhi ({\mathcal {H}}_w))$. Then, any partition of ${\mathcal {H}}$ is a partition of $\mathcal {QFZ}(G', \varPhi ({\mathcal {H}}_w))$. By the definition of saliency maps, we can affirm that any partition of $\mathcal {QFZ}(G, \varPhi ({\mathcal {H}}))$ is a partition of $\mathcal {QFZ}(G', \varPhi ({\mathcal {H}}_w))$.

In the following, we will prove that the three statements hold true for $\prec$.

• 1. We will first prove that $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}))$. By contradiction, let us assume that $G'$ is not a MST of $(G,\varPhi ({\mathcal {H}}))$. Then, by Lemma 49, there is an edge $u=\{x,y\}$ such that u is in $E{\setminus } E(G')$ and such that $\varPhi ({\mathcal {H}})(u)$ is different from the greatest weight among the edges in the path $\pi$ from x to y in $(G',\varPhi ({\mathcal {H}}))$. Let v be an edge of greatest weight in $\pi$. As ${\mathcal {H}}$ is equal to $\mathcal {QFZ}(G, \varPhi ({\mathcal {H}}))$, we may affirm that $\varPhi ({\mathcal {H}})(u)$ is lower than $\varPhi ({\mathcal {H}})(v)$ because, otherwise, the vertices x and y would be connected in the $\lambda$-level set of $(G, \varPhi ({\mathcal {H}}))$ for a $\lambda$ lower than $\varPhi ({\mathcal {H}})(u)$, which contradicts the fact that $\varPhi ({\mathcal {H}})$ is a saliency map. Hence, we have $\varPhi ({\mathcal {H}})(u) < \varPhi ({\mathcal {H}})(v)$. Then, by Lemma 51, as ${\mathcal {H}}$ is a flattening of ${\mathcal {H}}_w$, we may conclude that $\varPhi ({\mathcal {H}}_w)(u) < \varPhi ({\mathcal {H}}_w)(v)$. Hence, the weight $\varPhi ({\mathcal {H}}_w)(u)$ is different from the greatest weight among the edges in the path $\pi$. Therefore, by Lemma 49, $G'$ is not a MST of $(G,\varPhi ({\mathcal {H}}_w))$, which contradicts our assumption. Hence, we may conclude that $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}))$.

• 2. We will now prove the second condition for ${\mathcal {H}}$ to be a flattened hierarchical watershed of (G, w). As ${\mathcal {H}}_w$ is one-side increasing for $\prec$, by the second condition of Definition 3, for any watershed-cut edge $u=\{x,y\}$ for $\prec$, we have $\varPhi ({\mathcal {H}}_w)(u)=0$. Then, for any partition $\mathbf{P }$ of ${\mathcal {H}}_w$, x and y belong to the same region of $\mathbf{P }$. Therefore, as any partition of ${\mathcal {H}}$ is a partition of ${\mathcal {H}}_w$, we can say that, for any partition $\mathbf{P }$ of ${\mathcal {H}}$, x and y belong to the same region of $\mathbf{P }$. Hence, the lowest $\lambda$ such that x and y are the same partition $\mathbf{P }_\lambda$ of ${\mathcal {H}}$ is zero. Hence, $\varPhi ({\mathcal {H}})(u)=0$.

• 3. We will now prove the third condition for ${\mathcal {H}}$ to be a flattened hierarchical watershed of (G, w). By the third statement of Definition 3, we have that, for any edge u in $E_\prec$, there exists a child R of $R_u$ such that $\varPhi ({\mathcal {H}}_w)(u) \ge \vee \{\varPhi ({\mathcal {H}}_w)(v) \mid R_v \subseteq R\}$. Let u be an edge in $E_\prec$ and let R be the child of $R_u$ such that $\varPhi ({\mathcal {H}}_w)(u) \ge \vee \{\varPhi ({\mathcal {H}}_w)(v) \mid R_v \subseteq R\}$. Let v be an edge in $E_\prec$ such that $R_v \subseteq R$. Then, $\varPhi ({\mathcal {H}}_w)(u) \ge \varPhi ({\mathcal {H}}_w)(v)$. Hence, by Lemma 51, $\varPhi ({\mathcal {H}})(u) \ge \varPhi ({\mathcal {H}})(v)$. Therefore, we may conclude that $\varPhi ({\mathcal {H}})(u) \ge \vee \{\varPhi ({\mathcal {H}})(v) \mid R_v \subseteq R\}$.$\square$

The following lemma corresponds to the backward implication of Property 14.

Lemma 53

Let ${\mathcal {H}}$ be a hierarchy on V and let $\prec$ be an altitude ordering for w such that:

• 1. $(V, E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$; and

• 2. for any edge u in $E_\prec$, if u is not a watershed-cut edge for $\prec$, then $\varPhi ({\mathcal {H}})(u) = 0$; and

• 3. for any edge u in $E_\prec$, there exists a child R of $R_u$ such that $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $R\}$, where $\vee \{\} = 0$.

Then, ${\mathcal {H}}$ is a flattened hierarchical watershed of (G, w).

In order to prove Lemma 53, we first state two auxiliary lemmas. From Property 10 of [6], we can deduce the following lemma linking binary partition hierarchies and MSTs.

Lemma 54

Let ${\mathcal {B}}$ be a binary partition hierarchy of (G, w). The graph $(V,E_\prec )$ is a MST of (G, w).

By Property 12 of [6] linking hierarchical watersheds and hierarchies induced by an altitude ordering and a sequence of minima, and by Lemma 21, we infer the following lemma.

Lemma 55

Let $G'$ be a MST of (G, w) and let ${\mathcal {H}}$ be a hierarchical watershed of $(G',w)$. Then, ${\mathcal {H}}$ is also a hierarchical watershed of (G, w).

Proof of Lemma 53

Let ${\mathcal {H}}$ be a hierarchy on V such that there is an altitude ordering $\prec$ for w such that:

• 1. $(V, E_\prec )$ is a MST of $(G,\varPhi ({\mathcal {H}}))$; and

• 2. for edge u in $E_\prec$, if u is not a watershed-cut edge for $\prec$, then $\varPhi ({\mathcal {H}})(u) = 0$; and

• 3. for edge u in $E_\prec$, there exists a child R of $R_u$ such that $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $R\}$, where $\vee \{\} = 0$.

We will prove that ${\mathcal {H}}$ is a flattened hierarchical watershed of (G, w). To this end, we will prove that there is a hierarchical watershed ${\mathcal {H}}_w$ of (G, w) such that any partition of ${\mathcal {H}}$ is also a partition of ${\mathcal {H}}_w$. Let $G'$ denote the graph $(V,E_\prec )$. By Lemma 54, $G'$ is a MST of (G, w). Moreover, by Lemma 55, given a hierarchical watershed ${\mathcal {H}}_w$ of a MST of (G, w), we can say that ${\mathcal {H}}_w$ is also a hierarchical watershed of (G, w). Hence, we can simply prove that there is a hierarchical watershed ${\mathcal {H}}_w$ of $(G',w)$ such that any partition of ${\mathcal {H}}$ is also a partition of ${\mathcal {H}}_w$.

To define the hierarchy ${\mathcal {H}}_w$, we first define a map f from $E_\prec$ into $\mathbb {R}$ such that f is one-side increasing for $\prec$. Since $G'$ is a tree, by the definition of saliency maps, we can say that f is the saliency map of the hierarchy $\mathcal {QFZ}(G',f)$. By Lemma 4, as f is one-side increasing for $\prec$, we may say that $\mathcal {QFZ}(G',f)$ is a hierarchical watershed of $(G',w)$.

In the map f, the edges which are not watershed-cut edges for $\prec$ are assigned to zero, and the watershed-cut edges for $\prec$ are ranked according to their weights in w and in $\varPhi ({\mathcal {H}})$. Let $\prec _2$ be a total ordering on the set $\{u$ is a watershed-cut edge for $\prec \}$ such that, for any two watershed-cut edges u and v for $\prec$, we have $u \prec _2 v$ if and only if $\varPhi ({\mathcal {H}})(u) < \varPhi ({\mathcal {H}})(v)$ or if $\varPhi ({\mathcal {H}})(u) = \varPhi ({\mathcal {H}})(v)$ and $u \prec v$. The map f is defined as follows:

$$\begin{aligned} f(u) = {\left\{ \begin{array}{ll} 0 &{}\quad \hbox {if}\ u\ {\hbox {is not a watershed-cut}}\\ &{}\quad \hbox {edge for}\ \prec \\ \hbox {rank of }u\ {\hbox {for}}\ \prec _2 &{}\quad {\hbox {otherwise}} \\ \end{array}\right. } \end{aligned}$$

(2)

We first demonstrate that f is one-side increasing for $\prec$.

• 1. By the definition of f, as there are $n-1$ watershed-cut edges for $\prec$, we can say that, for any i in $\{1, \ldots , n-1\}$, there is a watershed-cut edge u for $\prec$ such that the rank of u for $\prec _2$ is i and, consequently, $f(u)=i$. On the other hand, as w has at least one minimum, there is at least one edge e in $E_\prec$ such that e is not a watershed-cut edge for $\prec$ and such that $f(e)=0$. Hence, we have $\{f(e) \mid u \in E_\prec \} = \{0, \ldots , n-1\}$. Therefore, the statement 1 of Definition 3 holds true for f.

• 2. For any edge u, by the definition of f, f(u) is nonzero if and only if u is not a watershed-cut edge for $\prec$, so the statement 2 of Definition 3 holds true for f.

• 3. Let u be a building edge for $\prec$. If u is not a watershed-cut edge for $\prec$, then there is a child X of $R_u$ such that there is no minimum of w included in X. Hence, none of the building edges of the descendants of X is a watershed-cut edge for $\prec$. By the definition of f, we have $f(u) = 0$ and, for any edge v such that $R_v \subseteq X$, we have $f(v) = 0$. Hence, $f(u) \ge \vee \{ f(v)$ such that $R_v$ is included in $X\}$. Otherwise, let us assume that u is a watershed-cut edge for $\prec$. Then, there is at least one minimum of w included in each child of $R_u$. By the hypothesis 3, there is a child X of $R_u$ such that $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $X\}$. Let X be the child of $R_u$ such that $\varPhi ({\mathcal {H}})(u) \ge \vee \{ \varPhi ({\mathcal {H}})(v)$ such that $R_v$ is included in $X\}$. Let e be a building edge for $\prec$ such that $R_e \subseteq X$. If e is not a watershed-cut edge for $\prec$, then $f(e) = 0$ and, consequently, $f(u) > f(e)$. Otherwise, if e is a watershed-cut edge for $\prec$, then we have $\varPhi ({\mathcal {H}})(u) \ge \varPhi ({\mathcal {H}})(e)$ and $e \prec u$, which implies that $e \prec _2 u$. Consequently, by the definition of f, we have $f(u) > f(e)$. Therefore, $f(u) \ge \vee \{ f(v)$ such that $R_v$ is included in $X\}$. Then, the third condition of Definition 3 holds true for f.

Hence, f is one-side increasing for $\prec$ and, as stated previously, $\mathcal {QFZ}(G',f)$ is a hierarchical watershed of $(G',w)$ (resp. (G, w)). Now, we only need to prove that any partition of ${\mathcal {H}}$ is a partition of $\mathcal {QFZ}(G',f)$. By the hypothesis 1, $G'$ is a MST of $(G,\varPhi ({\mathcal {H}}))$. Then, by Lemma 21, we can say that ${\mathcal {H}}$ is the QFZ hierarchy of $(G',\varPhi ({\mathcal {H}}))$. We will prove that any partition of $\mathcal {QFZ}(G',\varPhi ({\mathcal {H}}))$ is also a partition of $\mathcal {QFZ}(G',f)$.

Let the range of $\varPhi ({\mathcal {H}})$ be the set $\{0, \ldots , \ell \}$: $\{\varPhi ({\mathcal {H}})(u) \mid u \in E_\prec \} = \{0, \ldots , \ell \}$. Let $\lambda$ be a value in $\{0, \ldots , \ell \}$. Let $G'_{\lambda ,\varPhi ({\mathcal {H}})}$ be the $\lambda$-level set of $(G', \varPhi ({\mathcal {H}}))$. Let $\alpha$ be the greatest value in $\{f(u) \mid u \in E(G'_{\lambda ,\varPhi ({\mathcal {H}})})\}$. We will prove that the $\alpha$-level set of $(G',f)$ is equal to the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$. Since $\alpha$ is the greatest value in the set $\{f(u) \mid u \in E(G'_{\lambda ,\varPhi ({\mathcal {H}})})\}$, we can see that any edge v in the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$ also belongs to the $\alpha$-level set of $(G',f)$. Now, we also need to prove that there is no edge u in the $\alpha$-level set of $(G',f)$ such that u is not in the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$.

Let u be an edge which is not in the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$. Then, $\varPhi ({\mathcal {H}})(u) > \lambda$ and, for any edge v in the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$, we have $\varPhi ({\mathcal {H}})(u) > \varPhi ({\mathcal {H}})(v)$. Since the minimum value of $\lambda$ is zero, we can say that $\varPhi ({\mathcal {H}})(u) > 0$ and, by the hypothesis 2, u is a watershed-cut edge for $\prec$. Let v be an edge in the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$. Since $\varPhi ({\mathcal {H}})(u) > \varPhi ({\mathcal {H}})(v)$, if v is a watershed-cut edge for $\prec$, then $v \prec _2 u$ and $f(u) > f(v)$. Otherwise, if v is not a watershed-cut edge for $\prec$, by the definition of f, we have $f(v) = 0$ and $f(u) > f(v)$. Thus, for any edge v in the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$, we have $f(u) > f(v)$ and, therefore, $f(u) > \alpha$. Then, u is not in the $\alpha$-level set of $(G',f)$.

Therefore, we can conclude that the $\alpha$-level set of $(G',f)$ is equal to the $\lambda$-level set of $(G',\varPhi ({\mathcal {H}}))$. As the partitions of ${\mathcal {H}}$ are given by the set of connected components of the level sets of $(G', \varPhi ({\mathcal {H}}))$, we can affirm that any partition of ${\mathcal {H}}$ is also a partition of $\mathcal {QFZ}(G',f)$. Therefore, there is a hierarchical watershed ${\mathcal {H}}_w = \mathcal {QFZ}(G',f)$ of $(G',w)$ (resp. (G, w)) such that any partition of ${\mathcal {H}}$ is also a partition of ${\mathcal {H}}_w$. Then, ${\mathcal {H}}$ is a flattened hierarchical watershed of $(G',w)$ (resp. (G, w)). $\square$