Abstract
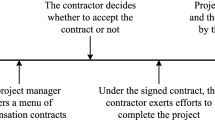
This paper investigates the impact of decision criteria on incentives in a project management setting, where a project manager operates a project consisting of two tasks performed sequentially by two different subcontractors. The completion time is characterized as an uncertain variable, which depends on the subcontractor’s unobservable effort of each task. Within the framework of uncertainty theory, four classes of uncertain principal agent models are presented under the expected value criterion and the critical value criterion. According to the structural characteristics, each model can be decomposed into two equivalent sub-models, which can be solved to obtain the optimal deadline-based incentive contracts via a two-step optimization method. Further, the interconnections among these contracts are discussed. It’s demonstrated that the optimal deadline-based incentive contract depends on the confidence level of the party (either the project manager or the subcontractor) who adopts the critical value criterion. Meanwhile, the more conservative the subcontractor is, the higher the incentive coefficients will be. And the more conservative the project manager is, the lower the incentive coefficients will be. Finally, given some special confidence levels, it’s interesting to find that the four models can be equivalent.




Similar content being viewed by others
References
Ayaǧ, Z. (2014). An integrated approach to concept evaluation in a new product development. Journal of Intelligent Manufacturing. doi:10.1007/s10845-014-0930-7.
Bayiz, M., & Corbett, C.J. (2005). Coordination and incentive contracts in project management under asymmetric information. Working paper, UCLA Anderson School.
Elmaghraby, S. E. (1990). Project bidding under deterministic and probabilistic activity durations. European Journal of Operational Research, 49(1), 14–34.
Fulkerson, D. R. (1961). A network flow computation for project cost curves. Management Science, 7(2), 167–179.
Gutierrez, G., & Paul, A. (2000). Analysis of the effects of uncertainty, risk-pooling, and subcontracting mechanisms on project performance. Operations Research, 48(6), 927–938.
Ke, H., Ma, J., & Tian, G. (2014). Hybrid multilevel programming with uncertain random parameters. Journal of Intelligent Manufacturing. doi:10.1007/s10845-014-0985-5.
Kelley, J. E. (1961). Critical path planning and scheduling: Mathematical basis. Operations Research, 9(3), 296–320.
Kwon, H. D., Lippman, H. D., & Tang, C. S. (2010). Optimal time-based and cost-based coordinated project contracts with unobservable work rates. International Journal of Production Economics, 126(2), 247–254.
Kwon, H. D., Lippman, S. A., & Tang, C. S. (2011). Sourcing decisions of project tasks with exponential completion times: Impact on operating profits. International Journal of Production Economics, 134(1), 138–150.
Lan, Y., Zhao, R., & Tang, W. (2011). A bilevel fuzzy principal-agent model for optimal nonlinear taxation problems. Fuzzy Optimization and Decision Making, 10(3), 211–232.
Li, X., & Wong, H. (2010). Credibilistic satisfiability and credibilistic entailment. Journal of Multi-Valued Logic and Soft Computing, 16(1–2), 105–134.
Li, X., & Liu, B. (2009a). Foundation of credibilistic logic. Fuzzy Optimization and Decision Making, 8(3), 91–102.
Li, X., & Liu, B. (2009b). Hybrid logic and uncertain logic. Journal of Uncertain Systems, 3(2), 83–94.
Liu, B. (2009). Some research problems in uncertainty theory. Journal of Uncertain Systems, 3(1), 3–10.
Liu, B. (2010). Uncertainty theory: A branch of mathematics for modeling human uncertainty. Berlin: Springer.
Liu, B. (2007). Uncertainty theory (2nd ed.). Berlin: Springer.
Liu, B. (2011). Uncertain logic for modeling human language. Journal of Uncertain Systems, 5(1), 3–20.
Liu, B. (2013a). Polyrectangular theorem and independence of uncertain vectors. Journal of Uncertainty Analysis and Applications, 1, 9.
Liu, Y. (2013b). Uncertain random variables: A mixture of uncertainty and randomness. Soft Computing, 17(4), 625–634.
Liu, B. (2015). Uncertainty theory (4th ed.). Berlin: Springer.
Mu, R., Lan, Y., & Tang, W. (2013). An uncertain contract model for rural migrant worker’s employment problems. Fuzzy Optimization and Decision Making, 12(1), 29–39.
Paul, A., & Gutierrez, G. (2005). Simple probability models for project contracting. European Journal of Operational Research, 165(2), 329–338.
Wang, G., Tang, W., & Zhao, R. (2013). An uncertain price discrimination model in labor market. Soft Computing, 17(4), 579–585.
Wu, X., Zhao, R., & Tang, W. (2013). Uncertain agency models with multi-dimensional incomplete information based on confidence level. Fuzzy Optimization and Decision Making, 13(2), 231–258.
Yang, K., & Liu, Y. (2014). Developing equilibrium optimization methods for hub location problems. Soft Computing. doi:10.1007/s00500-014-1427-1.
Yang, X., & Gao, J. (2013). Uncertain differential games with application to capitalism. Journal of Uncertainty Analysis and Applications, 1, 17.
Yang, K., Liu, Y., & Yang, G. (2014). Optimizing fuzzy \(p\)-hub center problem with generalized value-at-risk criterion. Applied Mathematical Modelling, 38(15–16), 3987–4005.
Yang, K., Zhao, R., & Lan, Y. (2014). The impact of risk attitude in new product development under dual information asymmetry. Computers & Industrial Engineering, 76(10), 122–137.
Yang, X., & Gao, J. (2014). Uncertain core for coalitional game with uncertain payoffs. Journal of Uncertain Systems, 8(2), 13–21.
Yang, L., Liu, P., Li, S., Gao, Y., & Ralescu, D. (2015). Reduction methods of type-2 uncertain variables and their applications to solid transportation problem. Information Sciences, 291, 204–237.
Zhu, Y. (2010). Uncertain optimal control with application to a portfolio selection model. Cybernetics and Systems, 41(7), 535–547.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant No. 71271151, No. 71301114 and No. 71471126, and the Research Fund for the Specialized Research Fund for the Doctoral Program of Higher Education under Grant No. 20130032110015.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, J., Yang, K. & Zhao, R. The impact of decision criteria on deadline-based incentive contracts in project management. J Intell Manuf 28, 643–655 (2017). https://doi.org/10.1007/s10845-014-0994-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-014-0994-4