Abstract
Maximum flow is one of the fundamental problems in graph theory with several applications such as bipartite matchings, image segmentation, disjoint paths, network connectivity, etc. Goldberg-Tarjan’s well-known Push Relabel (PR) Algorithm calculates the maximum s–t (source–target) flow on a directed weighted graph. PR algorithm has been effectively parallelized on GPUs. However, computing the maximum flow even using the GPU parallel PR algorithm continues to be time-consuming for large graphs. For the maximum flow algorithm’s error-tolerant applications, it is sufficient to compute the approximate maximum flow value. In this work, we propose multiple techniques for improving the push-relabel algorithm’s performance on the GPUs keeping its error-tolerant applications in mind. Our proposed techniques improve performance by carefully reducing the impact of the particular property that hampers the performance of the GPU parallel PR algorithm. These techniques provide tunable knobs to control the amount of approximation added and the respective performance achieved. In the end, we propose the Pull Relabel algorithm, which is the natural symmetric counterpart of the Push Relabel algorithm. Further, we combine both algorithms to construct a Pull-Push Relabel maxflow algorithm and analyze its effect on the dynamically changing graphs. We illustrate the effectiveness of our proposed algorithm and techniques using several real-world and synthetic graphs from the DIMACS Challenge, SNAP, Konect, and Network Repository, along with three maximum flow applications (Maximum Bipartite Matching, Team Elimination Problem, and Supply–Demand Problem). The proposals achieve 1.05\(\times\) to 94.83\(\times\) speedup over the exact GPU parallel push-relabel algorithm, and 14.29\(\times\), 40.40\(\times\) and 32.41\(\times\) speed-up on the three applications.






























Similar content being viewed by others
Notes
Our code is publicly available at https://github.com/Jash-Khatri/IJPP.
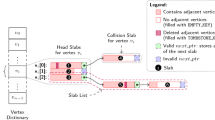
We note that the observations made in the following properties are well-known, and not ours. However, most of the earlier works on parallel max-flow computation have not exploited these properties, to the best of our knowledge, towards approximation and optimization.
References
Bader, D., Sachdeva, V.: A cache-aware parallel implementation of the push-relabel network flow algorithm and experimental evaluation of the gap relabeling heuristic. ISCA PDCS, p. 8, 01 (2005)
Anderson, R.J., Setubal, J.C.: On the parallel implementation of Goldberg’s maximum flow algorithm. In: Proceedings of the Fourth Annual ACM Symposium on Parallel Algorithms and Architectures, SPAA’92, pp. 168–177, New York, NY, USA (1992). Association for Computing Machinery
Dinitz, Yefim: Algorithm for solution of a problem of maximum flow in networks with power estimation. Sov. Math. Dokl. 11, 1277–1280 (1970)
Karzanov, Alexander: Determining the maximal flow in a network by the method of preflows. Doklady Math. 15, 434–437 (1974)
He, Z., Hong, B.: Dynamically tuned push-relabel algorithm for the maximum flow problem on cpu-gpu-hybrid platforms. In: 2010 IEEE International Symposium on Parallel Distributed Processing (IPDPS), pp. 1–10 (2010)
Edmonds, Jack, Karp, Richard M.: Theoretical improvements in algorithmic efficiency for network flow problems. J. ACM 19(2), 248–264 (1972)
Goldberg, Andrew V.: Recent developments in maximum flow algorithms (invited lecture). In: Proceedings of the 6th Scandinavian Workshop on Algorithm Theory, SWAT’98, pp. 1–10. Springer, Berlin, Heidelberg (1998)
Goldberg, Andrew V., Tarjan, Robert E.: A new approach to the maximum-flow problem. J. ACM 35(4), 921–940 (1988)
Hussein, M., Varshney, A., Davis, L.: On implementing graph cuts on cuda. First Workshop on General Purpose Processing on Graphics Processing Units, pp. 10, 10 (2009)
Karp, R.M., Vazirani, U.V., Vazirani, V.V.: An optimal algorithm for on-line bipartite matching. In: Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, STOC’90, pp. 352–358, New York, NY, USA (1990). Association for Computing Machinery
Wang, Y., Davidson, A., Pan, Y., Wu, Y., Riffel, A., Owens, J.D.: Gunrock: a high-performance graph processing library on the gpu. SIGPLAN Not. 51(8), 2016 (2016)
Luo, L., Wong, M., Hwu, W.: An effective gpu implementation of breadth-first search. In: Proceedings of the 47th Design Automation Conference, DAC’10, New York, NY, USA, pp. 52–55 (2010). Association for Computing Machinery
Bader, D.A., Madduri, K.: Gtgraph : A synthetic graph generator suite. http://www.cse.psu.edu/~madduri/software/GTgraph (2006)
Johnson, David S., McGeoch, Catherine C.: Network Flows and Matching: First DIMACS Implementation Challenge. American Mathematical Society, USA (1993)
Cormen, Thomas H., Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford: Introduction to Algorithms, 3rd edn. The MIT Press, Cambridge (2009)
Konect. http://konect.cc/networks/
Ford, D.R., Fulkerson, D.R.: Flows in Networks. Princeton University Press, Princeton (2010)
Vineet, V., Narayanan, P.J.: Cuda cuts: Fast graph cuts on the gpu. In: 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, pp. 1–8 (2008)
Hong, B.: A lock-free multi-threaded algorithm for the maximum flow problem. In: 2008 IEEE International Symposium on Parallel and Distributed Processing, pp. 1–8 (2008)
Mittal, Sparsh: A survey of techniques for approximate computing. ACM Comput. Surv. 48(4), 2016 (2016)
Besta, M., Weber, S., Gianinazzi, L., Gerstenberger, R., Ivanov, A., Oltchik, Y., Hoefler, T.: Slim graph: Practical lossy graph compression for approximate graph processing, storage, and analytics. In: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC’19, New York, NY, USA (2019). Association for Computing Machinery
Singh, S., Nasre, R.: Graffix: Efficient graph processing with a tinge of gpu-specific approximations. In: 49th International Conference on Parallel Processing - ICPP, ICPP’20, New York, NY, USA (2020). Association for Computing Machinery
Singh, S., Nasre, R.: Optimizing graph processing on gpus using approximate computing: Poster. In: Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming, PPoPP’19, pp. 395–396, New York, NY, USA (2019). Association for Computing Machinery
Princeton cos 226 course. https://www.cs.princeton.edu/courses/archive/spr03/cs226/assignments/baseball.html
Kaggle. https://www.kaggle.com
Acknowledgements
We thank the anonymous reviewers for their helpful comments which considerably improved the overall work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The last author is partially supported by NSM Grant CS/1920/1123/MEIT/008606.
Appendix A: Additional Maximum Flow Applications
Appendix A: Additional Maximum Flow Applications
1.1 A.1 Application 2: Team Elimination
Another application of maxflow is Team Elimination. In this use case, given a set of teams that play together in a league format, the objective is to find out if a given team is eliminated or not at any point in time. At any given moment, the i\(^{th}\) team has w[i] wins and g[i][j] games left to play against team j. A team is eliminated if it cannot possibly finish the season in the first place or tied for the first place. Our goal is to determine which teams are eliminated. Consider an example [24] presented in Table 5, having four teams. The columns indicate the number of wins, losses, the number of remaining games, and against whom the games would be played. Team-1 already has 83 wins (which is the highest so far) and has 8 games left (1 against Team-2, 6 against Team-3, and 1 against Team-4). Team-1 cannot be eliminated. Team-4 can finish with at most 80 wins (77 current wins + 3 games remaining). But Team-1 already has 83 wins. Hence, Team-4 can be eliminated. A more complex scenario occurs for Team-2. Team-2 can finish the season with as many as 83 wins, which appears to be enough to tie with Team-1. But this would require Team-1 to lose all of its remaining games, including the six against Team-3, in which case Team-3 would finish with 84 wins. Hence, Team-2 can also be eliminated.
Team Elimination can be reduced to maxflow. To check if a particular team x is eliminated or not, we create a flow network corresponding to that team and then run the maximum flow algorithm on it. In the generated flow network for a given team x, we have one node for each pair (i, j) denoted as i-j, of teams which are called game nodes, excluding team x. Similarly, we have nodes corresponding to each team except team x, which are called team nodes. We connect an artificial source s to each game node i-j and set its capacity to g[i][j] (number of games left for i to play against j). We then connect each game node i-j with the respective team nodes i and j and set the edge’s capacity to infinity (INF as shown in Fig. 31). Finally, we connect each team node to an artificial sink t. We include an edge from \(i^{th}\) team node to the sink with capacity w[x] + r[x] - w[i], where r[x] is the number of remaining games for team x. Based on the above explanation, the flow network generated for Team-4 given in the Table 5 is shown in Fig. 31. Note that the flow network generated for any team will always have four layers where Layer 1 has only the source, Layer 4 has only the sink, and layer 2 and layer 3 have \((n - 1)(n - 2)/2\) and \((n - 1)\) vertices respectively, where n is the total number of teams.
To check if the team is eliminated or not, we check if the maximum flow in the generated network saturates the arcs leaving the source vertex s. If the maximum flow does not saturate all the arcs leaving s, then there is no scenario in which team x wins the division. Hence such a team can be eliminated. For the example graph shown in Fig. 31, maxflow from s to t is 2, and it does not saturate all the outgoing edges from s. This is because the sum of the edge weights of all the outgoing edges from s is 7. So Team-4 can be eliminated.
1.1.1 A.1.1 Push Relabel Algorithm on Team Elimination Application
We experimented with real-world leagues [25]. However, they have a maximum of 25–30 teams, leading to small maxflow networks. Hence, computing maxflow for these cases was extremely fast. Therefore, it was statistically not useful to compare the non-optimized and the optimized versions. Therefore, we resorted to generating larger datasets. We synthesized data for a league that has 1500 teams with a random distribution. This led to the creation of 1500 graphs, each of size approximately 1 million vertices and 3 million edges. Out of these 1500 graphs, we ran the algorithm on a random set of 25 graphs and collected the results. For the purpose of evaluation, we call the baseline Push Relabel algorithm as Algorithm A (exact) and the Push Relabel Algorithm with our set of techniques applied as Algorithm B (approximate). We apply all our techniques discussed in Sect. 3 on the top of Algorithm A, naming the modified algorithm as Algorithm B.
We use two criteria for evaluating our techniques: inaccuracy in Fig. 32 and execution time in Fig. 33. From Fig. 32, we can observe that the maximum flow value generated by Algorithm B is very close to that by Algorithm A. On an average, we observe an accuracy loss of 0%. Also, we observe that the average execution time for Algorithm A is 27.951 s, while that for Algorithm B is 0.692 s. On an average, Algorithm B achieves a geomean speedup of 40.4\(\times\), clearly indicating the benefits of our proposals.
1.2 A.2 Application 3: Supply Demand Problem
The third application is supply–demand in road networks. Given a road network, each vertex represents a physical location, edges between nodes represent the roads connecting the physical locations, and each edge has a capacity that represents the number of items that can be sent via that road. Nodes are of three types: (i) supply nodes which are locations generating the items with some capacity, (ii) demand nodes which are locations needing a certain number of these items, and (iii) regular nodes which are neither supply nodes nor demand nodes but act as transit junctions. The optimization problem is to find out the maximum amount of goods that can be sent from supply nodes to demand nodes through the road network.
Figure 34 (left) presents an example of a road network with two supply nodes and two demand nodes. Now, let us consider the following supply and demand values:
-
Node 1 Supply Rate: 20
-
Node 2 Supply Rate: 80
-
Node 5 Demand Rate: 30
-
Node 6 Demand Rate: 95
For converting this into an applicable maxflow network, we generate one extra node as a source (S) and connect it to all the supply nodes with edge capacities equal to the supply rate of the respective supply node. Similarly, we generate one extra node as a sink (T) and connect it to all the demand nodes with edge capacities equal to the demand rate of the respective demand node. Once we have constructed the flow network as stated above, we run the push-relabel algorithm on it. The flow network constructed for the example is shown in Fig. 34 (right).
In our implementation, we use synthetic graphs to test the application. We generate road networks with 100,000 nodes and approximately 200,000 edges. We generate a random number from the range [1, 100] to assign edge capacities of the original road network. For each run of the algorithm, a random and disjoint sets of supply and demand nodes are generated, each with a randomly generated supply and demand capacity.
As in the first application, we use two criteria for evaluating our techniques: speedup and inaccuracy. We name the baseline maximum flow algorithm as Algorithm A. We apply all our techniques discussed in Sect. 3 to the baseline, naming the modified algorithm as Algorithm B. We consider the maxflow value generated by Algorithm A to be the actual maximum flow and observe the loss in accuracy of the maxflow values computed by Algorithm B. Figure 35 shows the relative error of maximum flow computation by Algorithm B. From Fig. 35, we observe that the maximum flow value generated by Algorithm B is primarily the same as that of Algorithm A. On an average, we observe an accuracy loss of 0% in the maximum flow values computed by Algorithm B.
Figure 36 compares performance of the two algorithms. We observe that the average execution time for Algorithm A is 1.773 s, while that for Algorithm B is 0.06 s. On an average, we observe a geomean speedup of 32.41\(\times\) due to our proposed techniques, clearly indicating their benefit.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Khatri, J., Samar, A., Behera, B. et al. Scaling the Maximum Flow Computation on GPUs. Int J Parallel Prog 50, 515–561 (2022). https://doi.org/10.1007/s10766-022-00740-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10766-022-00740-7