iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s10766-015-0380-7
Memory Partitioning in the Limit | International Journal of Parallel Programming Skip to main content

Advertisement

Springer Nature Link
Log in

Memory Partitioning in the Limit

  • Published:
International Journal of Parallel Programming Aims and scope Submit manuscript

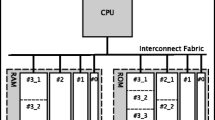
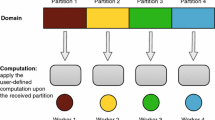
Abstract

The key difficulties in designing memory hierarchies for future computing systems with extreme scale parallelism include (1) overcoming the design complexity of system-wide memory coherence, (2) achieving low power, and (3) achieving fast access times within such a memory hierarchy. Towards addressing these difficulties, in this paper we propose an automatic memory partitioning method to generate a customized, application-specific, energy-efficient, low latency memory hierarchy, tailored to particular application programs. Given a software program to accelerate, our method automatically partitions the memory of the original program, creates a new customized application-specific multi-level memory hierarchy for the program, and modifies the original program to use the new memory hierarchy. This new memory hierarchy and modified program are then used as the basis to create a customized, application-specific, highly parallel hardware accelerator, which is functionally equivalent to the original, unmodified program. Using dependence analysis and fine grain valid/dirty bits, the memories in the generated hierarchy can operate in parallel without the need for maintaining coherence and can be independently initialized/flushed from/to their parent memories in the hierarchy, enabling a scalable memory design. The generated memories are fully compatible with the memory addressing in the original software program; this compatibility feature enables the translation of general software applications to application-specific accelerators. We also provide a compiler analysis method to perform accurate dependence analysis for memory partitioning based on symbolic execution, and a profiler-based futuristic limit study to identify the maximum gains that can be achieved by memory partitioning.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Notes

  1. Due to past progress in the binary translation and optimization field, the binary instructions of an ISA are by now a de facto compiler intermediate language [17, 18, 43] which allows access to a wide range of applications.

  2. A compiler algorithm answering memory disambiguation questions without any mistakes is impossible. Assume by way of contradiction that there were such an algorithm f such that \(f(p,I_1,I_2)\) precisely determines whether the following statement is valid “there exists an execution/initial state of program p where an instance of \(I_1\) executes and an instance of \(I_2\) executes and these instances refer to the same memory location”. Then, by Kleene’s (second) recursion theorem [40], a “contrarian” program can be constructed which runs the algorithm f on itself, and its memory instructions \(I_1\) and \(I_2\), before ever executing \(I_1\) and \(I_2\), and then, after getting f’s answer, executes its remaining part: (1) making \(I_1,I_2\) independent regardless of the initial state, if the algorithm f responds with YES (\(I_1,I_2\) are dependent), and (2) making \(I_1,I_2\) dependent on at least one initial state, if the algorithm f responds with NO (\(I_1,I_2\) are independent). Contradiction. Therefore, no such algorithm f exists. Therefore, even though many current compiler algorithms are able to avoid false negative mistakes (i.e., mistakes which say there is no dependence when in fact there is), any disambiguation algorithm attempting to approximate f must on some inputs either not finish, or must make conservative (false positive) mistakes, and say \(I_1,I_2\) are dependent when they are not. But this negative result has not discouraged compiler researchers, since approximate memory disambiguation algorithms have done well enough.

  3. On scientific applications, e.g., loop nests containing arrays with affine subscripts, existing compiler transformations for parallelization and data localization on general purpose parallel processors could of course be used as a preprocessing step before applying our memory partitioning techniques for creating application-specific supercomputer hardware. For example, applying our technique on the loop for(int i=0; i \({\texttt {<}}\) nProc; ++i) func(i, data[i]); created by a typical sequential to parallel code transformation [1] for scientific code (parallelized SPMD code converted back to a sequential representation) will lead to loop i iterations being dispatched through our hierarchical software pipelining on an array of identical application-specific hardware units implementing func, each with its private child memory hierarchy representing a partition of the data array, without using any coherence hardware across child memory hierarchies, and without using power-hungry general purpose processors to implement func. Our techniques, however, are not limited to scientific applications.

  4. While the present work is a limit study, it is instructive to consider its practical implementation aspects. These aspects, including the implementation of parallel simultaneous accesses, will be addressed in Sect. 4.4.

  5. In the cache implementation, it is possible to save storage space by identifying duplicate, dead, and constant bits. When a bit within a cache data line (or address) can always be computed as a function of other fixed bits in the same data line (or, respectively, in the same address), no cache hardware resources are needed for that bit. The missing bit can be recreated by recomputing it when needed. Similarly, a bit proved by the compiler to be dead need not be stored as it will never be used, and a constant bit need not be stored as its value can always be predicted with perfect accuracy.

  6. An arbitrary multiple-entry, multiple-exit connected code fragment possibly spanning multiple procedures and files (e.g., the hot basic blocks of an executable) can be converted to a single-entry, single-exit code fragment resembling a procedure, by initially executing a multi-way branch based on the entry point address (program counter), and having all the original exits of the code fragment jump to a single return instruction. One can also use the profiler for discovering the most probable targets of indirect branches, when the target(s) cannot be found statically.

  7. In this work, we assume that the target procedure is either a leaf in the call graph, or it makes calls only to functions with an equivalent hardware version in our component library (e.g., max(a, b)).

  8. We provide a definition for dependence in Sect. 5.

  9. This definition includes input dependences. Excluding input dependences (requiring at least one of \(I_1\) or \(I_2\) to be a store operation) can result in a partitioned memory where more than one copy of a data can exist in the system. However, this case occurs only for data that is exclusively accessed using load instructions (i.e., read-only data), in which case there is still no need for maintaining coherence across memories.

  10. As already summarized in Sect. 3.2, existing symbolic execution methods [21] define a program fact as a mapping from variable names to their values, such as (var, val) mapping variable var to its value val. We modified this definition to record program facts involving variables without names and pointers, such as (ptr, val) which maps the location pointed by ptr to val. We can still capture variable to value mapping information, albeit at a slightly modified form, such as \( ( \& var,val)\), where \( { \& }var\) is the address expression for variable var.

  11. The basic blocks are traversed based on their reverse post ordering numbers.

  12. Termination of this algorithm can simply be proven using the fact that a program can have a finite number of induction variables. The maximum number of iterations done by our algorithm depends on the length of the longest induction variable dependence chain in the target procedure.

  13. Solving induction variables of inner loops before outer loops enables us to solve higher order induction variables.

  14. We also solve loop exit conditions to find the symbolic loop trip counts, which correspond to the maximum values for loop index variables (i.e., \(I_{max}\) values where \(0 \le I < I_{max}\)).

  15. In our implementation, we use the symbol information embedded into the assembly files by gcc when the gstabs+ option is used.

  16. If the values on both states are the same, the expression simplification algorithm eliminates the conditional expression, i.e., simplify(cond ? x : x) = x.

References

  1. Anderson, Jennifer M., Amarasinghe, Saman P., Lam, Monica S.: Data and computation transformations for multiprocessors. In: Proceedings of the Fifth ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPOPP ’95, pp. 166–178, New York, NY, USA. ACM (1995)

  2. Anderson, Jennifer M., Lam, Monica S.: Global optimizations for parallelism and locality on scalable parallel machines. In: Proceedings of the ACM SIGPLAN 1993 Conference on Programming Language Design and Implementation, PLDI ’93, pp. 112–125 (1993)

  3. Avissar, Oren, Barua, Rajeev, Stewart, Dave: An optimal memory allocation scheme for scratch-pad-based embedded systems. ACM Trans. Embed. Comput. Syst. 1(1), 6–26 (2002)

    Article  Google Scholar 

  4. Banakar, R., Steinke, S., Lee, B.-S., Balakrishnan, M., Marwedel, P.: Scratchpad memory: design alternative for cache on-chip memory in embedded systems. In: Proceedings of the Tenth International Symposium on Hardware/software codesign, CODES ’02, (2002)

  5. Banerjee, U.K.: Dependence Analysis for Supercomputing. Kluwer Academic Publishers, Norwell (1988)

    Book  Google Scholar 

  6. Baradaran, Nastaran, Diniz, Pedro C.: A compiler approach to managing storage and memory bandwidth in configurable architectures. ACM Trans. Des. Autom. Electron. Syst. 13(4), 61:1–61:26 (2008)

    Article  Google Scholar 

  7. Benini, L., Macchiarulo, L., Macii, A., Poncino, M.: From architecture to layout: partitioned memory synthesis for embedded systems-on-chip. In: Proceedings of Design Automation Conference, 2001, pp. 784–789 (2001)

  8. Benini, L., Macii, A., Poncino, M.: A recursive algorithm for low-power memory partitioning. In: Proceedings of the 2000 International Symposium on Low Power Electronics and Design, ISLPED ’00, pp. 78–83, ACM (2000)

  9. Blume, W., Eigenmann, R.: The range test: a dependence test for symbolic, non-linear expressions. In: Supercomputing ’94, (1994)

  10. Bobda, Christophe: Introduction to Reconfigurable Computing: Architectures, Algorithms, and Applications, 1st edn. Springer, New York (2007)

    Book  MATH  Google Scholar 

  11. Charles, P., Grothoff, C., Saraswat, V., Donawa, C., Kielstra, A., Ebcioglu, K., von Praun, C., Sarkar, V.: X10: an object-oriented approach to non-uniform cluster computing. In: Proceedings of the 20th Annual ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, OOPSLA ’05, pp. 519–538 (2005)

  12. Chen, T., Lin, J., Dai, X., Hsu, W.-C., Yew, P.-C.: Data dependence profiling for speculative optimizations. In: Evelyn Duesterwald (ed.) Compiler Construction, vol. 2985 of Lecture Notes in Computer Science, pp. 57–72 (2004)

  13. Cimitile, A., De Lucia, A., Munro, M.: Qualifying reusable functions using symbolic execution. In: Proceedings of the Second Working Conference on Reverse Engineering (1995)

  14. Coen-Porisini, A., De Paoli, F., Ghezzi, C., Mandrioli, D.: Software specialization via symbolic execution. IEEE Trans. Softw. Eng. 17(9), 884–889 (1991)

    Article  Google Scholar 

  15. Cong, J., Jiang, W., Liu, B., Zou, Y.: Automatic memory partitioning and scheduling for throughput and power optimization. In: Computer-Aided Design—Digest of Technical Papers, 2009. ICCAD 2009. IEEE/ACM International Conference on, pp. 697–704 (2009)

  16. Csallner, C., Tillmann, N., Smaragdakis, Y.: Dysy: dynamic symbolic execution for invariant inference. In: Proceedings of the 30th International Conference on Software Engineering (2008)

  17. Dehnert, J.C., Grant, B.K., Banning, J.P., Johnson, R., Kistler, T., Klaiber, A., Mattson, J.: The transmeta code morphing software: using speculation, recovery, and adaptive retranslation to address real-life challenges. In: Proceedings of the International Symposium on Code Generation and Optimization: Feedback-directed and Runtime Optimization, CGO ’03, pp. 15–24, Washington, DC, USA. IEEE Computer Society (2003)

  18. Ebcioğlu, K., Altman, E.R.: Daisy: dynamic compilation for 100% architectural compatibility. In: Proceedings of the 24th Annual International Symposium on Computer Architecture, ISCA ’97, pp. 26–37, New York, NY, USA. ACM (1997)

  19. El-Ghazawi, T., Cantonnet, F.: Upc performance and potential: a NPB experimental study. In: Proceedings of the 2002 ACM/IEEE Conference On Supercomputing, Supercomputing ’02, pp. 1–26 (2002)

  20. Elkarablieh, B., Godefroid, P., Levin, M.Y.: Precise pointer reasoning for dynamic test generation. In: ISSTA ’09: Proceedings of the Eighteenth International Symposium on Software Testing and Analysis (2009)

  21. Fahringer, T., Scholz, B.: A unified symbolic evaluation framework for parallelizing compilers. IEEE Trans. Parallel Distrib. Syst. 11(11), 1110–1125 (2000)

    Google Scholar 

  22. Feautrier, Paul: Dataflow analysis of array and scalar references. Int. J. Parallel Program. 20(1), 23–53 (1991)

    Article  MATH  Google Scholar 

  23. Gokhale, Maya B., Graham, Paul S.: Reconfigurable Computing: Accelerating Computation with Field-Programmable Gate Arrays, 1st edn. Springer, New York (2010)

    Google Scholar 

  24. Gokhale, M.B., Stone, J.M.: Automatic allocation of arrays to memories in fpga processors with multiple memory banks. In: Proceedings of the Seventh Annual IEEE Symposium on Field-Programmable Custom Computing Machines, FCCM ’99 (1999)

  25. Haghighat, M., Polychronopoulos, C.: Symbolic program analysis and optimization for parallelizing compilers. In: Banerjee, Utpal, Gelernter, David, Nicolau, Alex, Padua, David (eds.) Languages and Compilers for Parallel Computing, Volume 757 of Lecture Notes in Computer Science, pp. 538–562. Springer, Berlin (1993)

    Chapter  Google Scholar 

  26. Heinrich, J.: Origin and onyx2 theory of operations manual, silicon graphics corporation. Document number 007-3439-002, (1997). http://techpubs.sgi.com/library/manuals/3000/007-3439-002/pdf/007-3439-002.pdf

  27. Henning, J.L.: Spec cpu2006 benchmark descriptions. SIGARCH Comput. Arch. News 34(4), 1–17 (2006)

    Article  MathSciNet  Google Scholar 

  28. Huffman, D.A.: A method for the construction of minimum-redundancy codes. Proc. IRE 40(9), 1098–1101 (1952)

    Article  MATH  Google Scholar 

  29. Ketterlin, A., Clauss, P.: Profiling data-dependence to assist parallelization: framework, scope, and optimization. In: Proceedings of the 2012 45th Annual IEEE/ACM International Symposium on Microarchitecture, MICRO ’12 (2012)

  30. King, J.C.: Symbolic execution and program testing. Communications of ACM 19(7), 385–394 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  31. Krambeck, R.H., Lee, C.M., Law, H.-F.S.: High-speed compact circuits with cmos. IEEE J. Solid-State Circuits 17(3), 614–619 (1982)

    Article  Google Scholar 

  32. Larus, J.R.: Loop-level parallelism in numeric and symbolic programs. IEEE Trans. Parallel Distrib. Syst. 4(7), 812–826 (1993)

    Article  Google Scholar 

  33. Mahapatra, Nihar R., Liu, Jiangjiang, Sundaresan, Krishnan, Dangeti, Srinivas, Venkatrao, Balakrishna V.: A limit study on the potential of compression for improving memory system performance, power consumption, and cost. J. Instr. Level Parallelism 7, 1–37 (2005)

    Google Scholar 

  34. Moon, Soo-Mook, Ebcioğlu, Kemal: Parallelizing nonnumerical code with selective scheduling and software pipelining. ACM Trans. Program. Lang. Syst. 19(6), 853–898 (1997)

    Article  Google Scholar 

  35. Muralimanohar, N., Balasubramonian, R., Jouppi, N.P.: CACTI 6.0. http://www.hpl.hp.com/research/cacti/. (2009)

  36. Necula, G.C.: Translation validation for an optimizing compiler. SIGPLAN Not. 35(5), 83–94 (2000)

    Article  Google Scholar 

  37. Numrich, Robert W., Reid, John: Co-array fortran for parallel programming. SIGPLAN Fortran Forum 17(2), 1–31 (1998)

    Article  Google Scholar 

  38. Pugh, W.: The omega test: a fast and practical integer programming algorithm for dependence analysis. In: Proceedings of the 1991 ACM/IEEE Conference on Supercomputing, Supercomputing ’91, pp. 4–13, ACM (1991)

  39. Rinard, M.C., Diniz, P.C.: Commutativity analysis: a new analysis framework for parallelizing compilers. In: Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (1996)

  40. Rogers Jr, Hartley: Theory of Recursive Functions and Effective Computability. MIT Press, Cambridge (1987)

    MATH  Google Scholar 

  41. Rul, S., Vandierendonck, H., De Bosschere, K.: Towards automatic program partitioning. In: Proceedings of the 6th ACM Conference on Computing frontiers, CF ’09 (2009)

  42. Shannon, Claude E., Weaver, Warren: A Mathematical Theory of Communication. University of Illinois Press, Champaign (1963)

    MATH  Google Scholar 

  43. Silberman, Gabriel M., Ebcioglu, Kemal: An architectural framework for supporting heterogeneous instruction-set architectures. Computer 26(6), 39–56 (1993)

    Article  Google Scholar 

  44. So, B., Hall, M.W., Ziegler, H.E.: Custom data layout for memory parallelism. In: Proceedings of the International Symposium on Code Generation and Optimization: Feedback-Directed and Runtime Optimization, CGO ’04 (2004)

  45. Standard Performance Evaluation Committee. Spec cpu2000 benchmarks, (2000). http://www.spec.org/cpu2000/

  46. Tarjan, Robert Endre: Depth-first search and linear graph algorithms. SIAM J. Comput. 1(2), 146–160 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  47. Weinhardt, M., Luk, W.: Memory access optimization and ram inference for pipeline vectorization. In: FPL (1999)

  48. Yelick, K., Bonachea, D., Chen, W.-Y., Colella, P., Datta, K., Duell, J., Graham, S.L., Hargrove, P., Hilfinger, P., Husbands, P., Lancu, C., Kamil, A., Nishtala, R., Su, J., Welcome, M., Wen, T.: Productivity and performance using partitioned global address space languages. In: Proceedings of the 2007 International Workshop on Parallel Symbolic Computation, PASCO ’07 (2007)

  49. Yelick, K., Hilfinger, P., Graham, S., Bonachea, D., Su, J., Kamil, A., Datta, K., Colella, P., Wen, T.: Parallel languages and compilers: perspective from the titanium experience. Int. J. High Perform. Comput. Appl. 21(3), 266–290 (2007)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Pennsylvania State University, 111N IST Building, University Park, PA, 16802, USA

    Emre Kültürsay & Mahmut T. Kandemir

  2. Global Supercomputing Corporation, P.O. Box 603, Yorktown Heights, NY, 10598, USA

    Kemal Ebcioğlu

  3. Faculty of Engineering and Architecture, Yeditepe University, Office A-407, Kayisdagi, 34755, Istanbul, Turkey

    Gürhan Küçük

Authors
  1. Emre Kültürsay
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kemal Ebcioğlu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gürhan Küçük
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mahmut T. Kandemir
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Emre Kültürsay.

Appendix: Details of Symbolic Execution

Appendix: Details of Symbolic Execution

1.1 Basic Block Execute Algorithm

Figure 15 presents the pseudocode for the execute function referred to in Fig. 7. Given a basic block b, this function starts with the entry program state of b, executes all instructions in the basic block, and then generates one or more exit program states. Executing each instruction in the basic block has some side effects on the program state, updating the stored symbolic value expressions of some registers or memory locations recorded in the program state. The figure shows three types of instructions. The first one is an arithmetic operation which is handled by reading the value expressions corresponding to the two source registers, creating a simplified result expression, and updating the value of the corresponding destination register in the program state with this simplified result. The second one is a memory load instruction which starts with extracting the value expression of the source register (containing the operand address) from the program state, and then requires a lookup in the program state with this extracted value expression, which is treated as an address expression. Finally, the lookup result is used to update the value of the destination register. The third operation is a two-way branch the direction of which depends on the value a condition register. If the basic block ends with a two-way conditional branch, the symbolic value expression of the condition register obtained from the program state and its logical negation are used to update the path predicate expressions on the two outgoing edges of this basic block. Other types of instructions are variants of these three types of instructions and are omitted for brevity.

Fig. 15
figure 15

Symbolic execution execute algorithm for executing the instructions in a basic block

Full size image

1.2 Program State Join Algorithm

Figure 16 gives the pseudocode for the join function referred in Fig. 7 Given a basic block b, this function takes two program states on two (forward) CFG edges coming into b, and computes the program state that is valid at the entry point of b. When there are more than two incoming edges to a basic block, this function is called more than once (e.g., join(edge1, join(edge2,edge3)) for three incoming edges). The path predicate at the entry of b is obtained by performing a logical or operation on the incoming edge path predicates. For each address-to-value expression mappings on the first program state, the corresponding value expression on the second program state is obtained and a conditional expression is created.Footnote 16 The second loop handles the address-to-value expression mappings on the second program state that do not exist on the first program state (i.e., the address expressions not handled by the first loop). As a result of applying this join operation, the program state at the entry of basic block b is obtained, which is the input to the execute function given in Fig. 15. It is important to note that this algorithm is used only for joining forward edges. Backward edges define loops, which are handled by the algorithm in Fig. 7.

Fig. 16
figure 16

Symbolic execution join algorithm for joining the program states corresponding to two incoming forward CFG edges to a basic block

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kültürsay, E., Ebcioğlu, K., Küçük, G. et al. Memory Partitioning in the Limit. Int J Parallel Prog 44, 337–380 (2016). https://doi.org/10.1007/s10766-015-0380-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10766-015-0380-7

Keywords

Search

Navigation