Abstract
Timed automata are frequently used to model real-time systems. Their determinization is a key issue for several validation problems. However, not all timed automata can be determinized, and determinizability itself is undecidable. In this paper, we propose a game-based algorithm which, given a timed automaton, tries to produce a language-equivalent deterministic timed automaton, otherwise a deterministic over-approximation. Our method generalizes two recent contributions: the determinization procedure of Baier et al. (Proceedings of the 36th international colloquium on automata, languages and programming (ICALP’09), 2009) and the approximation algorithm of Krichen and Tripakis (Form Methods Syst Des 34(3):238–304, 2009). Moreover, we extend it to apply to timed automata with invariants and \(\varepsilon \)-transitions, and also consider other useful approximations: under-approximation, and combination of under- and over-approximations.

















Similar content being viewed by others
References
Alur R, Dill DL (1994) A theory of timed automata. Theor Comput Sci 126(2):183–235
Finkel O (2006) Undecidable problems about timed automata. In: Proceedings of the 4th international conference on formal modeling and analysis of timed systems (FORMATS’06) (Lecture Notes in Computer Science), vol 4202. Springer, pp. 187–199
Tripakis S (2006) Folk theorems on the determinization and minimization of timed automata. Inf Process Lett 99(6):222–226
Asarin E, Maler O, Pnueli A, Sifakis J (1998) Controller synthesis for timed automata. In: Proceedings of the 5th IFAC symposium on system structure and control (SSSC’98). Elsevier Science, Amsterdam, pp. 469–474
Alur R, Fix L, Henzinger TA (1994) A determinizable class of timed automata. In: Proceedings of the 6th international conference on computer aided verification (CAV’94) (Lecture Notes in Computer Science), vol 818. Springer, New York, pp 1–13
Vijay SP, Pandya PK, Narayanan KS, Lakshmi M (2008) Timed automata with integer resets: language inclusion and expressiveness. In: Proceedings of the 6th international conference on formal modeling and analysis of timed systems (FORMATS’08) (Lecture Notes in Computer Science), vol 5215. Springer, pp. 78–92
Baier C, Bertrand N, Bouyer P, Brihaye T (2009) When are timed automata determinizable? In: Proceedings of the 36th international colloquium on automata, languages and programming (ICALP’09) (Lecture Notes in Computer Science), vol 5556. Springer, Rhodes, pp. 43–54
Krichen M, Tripakis S (2009) Conformance testing for real-time systems. Form Methods Syst Des 34(3):238–304
Bouyer P, Chevalier F, D’Souza D (2005) Fault diagnosis using timed automata. In: Proceedings of the 8th international conference on foundations of software science and computational structures (FOSSACS’05) (Lecture Notes in Computer Science), vol 3441. Springer, San Diego, pp. 219–233
Bertrand N, Jéron T, Stainer A, Krichen M (2012) Off-line test selection with test purposes for non-deterministic timed automata. Log Methods Comput Sci 8(4:8):1
Bertrand N, Stainer A, Jéron T, Krichen M (2011) A game approach to determinize timed automata. In: Proceedings of the 14th international conference on foundations of software science and computation structures (FOSSACS’11) (Lecture Notes in Computer Science), vol 6604. Springer, pp. 245–259.
Grädel E, Thomas W, Wilke T (2002) (eds) Automata, logics, and infinite games: a guide to current research (Lecture Notes in Computer Science), (vol 2500). Springer, Berlin
Bouyer P, Dufourd C, Fleury E, Petit A (2004) Updatable timed automata. Theor Comput Sci 321(2–3):291–345
Lakshmi M, Narayanan KS (2010) Integer reset timed automata: clock reduction and determinizability. CoRR arXiv:1001.1215v1
Bouyer P (2004) Forward analysis of updatable timed automata. Form Methods Syst Des 24(3):281–320
Bertrand N, Jéron T, Stainer A, Krichen M (2011) Off-line test selection with test purposes for non-deterministic timed automata. In: Proceedings of the 17th international conference on tools and algorithms for the construction and analysis of systems (TACAS’11) (Lecture Notes in Computer Science), vol 6605. Springer, pp. 96–111
Alur R, Henzinger TA, Kupferman O, Vardi MY (1998) Alternating refinement relations. In: Proceedings of the 9th international conference on concurrency theory (CONCUR’98) (Lecture Notes in Computer Science), vol 1466. Springer, New York, pp 163–178
David A, Larsen KG, Legay A, Nyman U, Wasowski A (2010) Timed i/o automata: a complete specification theory for real-time systems. In: Proceedings of the 13th ACM international conference on hybrid systems: computation and control (HSCC’10). ACM, pp. 91–100
Acknowledgments
This work was partially funded by the TESTEC Project of the french research agency (ANR).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Proposition 2
Let us assume that \(Y\) is totally ordered, and for \(Y' \subseteq Y\), we write \(\min (Y')\) for the smallest element in \(Y'\) according to the total order, with the convention that \(\min (\emptyset ) = \emptyset \). Given a winning strategy \(\sigma :{\mathsf {V}}_D\rightarrow {\mathsf {Act}}_D\) for Determinizator, we define \(\sigma ':{\mathsf {V}}_D\rightarrow Y\cup \{\emptyset \}\), with atomic resets, iteratively. The idea is to simulate \(\sigma \) using only atomic resets. Instead of having several clocks with same value, we reset only one clock and use a mapping, along the construction, to store which clock is used to represent which set of clocks. Then, one considers triples with a state reached following \(\sigma '\), the corresponding state reached following \(\sigma \) and a mapping \(\gamma \) which assigns to each clock, the clock used in the state of \(\sigma '\) to represents its value in the state of \(\sigma \).
-
\({\mathsf {Temp}}:=\{({\mathsf {v}},{\mathsf {v}},\mathsf {Id})\in {\mathsf {V}}_D\times {\mathsf {V}}_D\times Y^Y\;|\; \exists (r,a)\in {\mathsf {Act}}_S \text{ s.t. } ({\mathsf {v}}_0,r,a,{\mathsf {v}})\in \delta \}\)
-
\({\mathsf {V}}_{\mathsf {def}} := \emptyset \)
-
While \({\mathsf {Temp}}\ne \emptyset \)
-
take \(({\mathsf {v}}',{\mathsf {v}},\gamma )\) in \({\mathsf {Temp}}\)
-
if \({\mathsf {v}}' \notin {\mathsf {V}}_{\mathsf {def}}\) then
-
\(\sigma '({\mathsf {v}}'):=\min (\sigma ({\mathsf {v}}))\)
-
\(\gamma '(y):= \left\{ \begin{array}{ll}\sigma '({\mathsf {v}}') &{} \text{ if } y \in \sigma ({\mathsf {v}}),\\ \gamma (y) &{} \text{ otherwise }\end{array}\right. \)
-
\({\mathsf {Temp}}:={\mathsf {Temp}}\cup \{({\mathsf {w}}',{\mathsf {w}},\gamma ')\;|\; \exists {\mathsf {v}}'_S,{\mathsf {v}}_S \in {\mathsf {V}}_S,\ \exists r'' \in {\mathsf {Reg}}_{M'}^Y,\ \exists b \in \varSigma \text{ s.t. } {\mathsf {v}}'\xrightarrow {\sigma '({\mathsf {v}}')}{\mathsf {v}}'_S\xrightarrow {(r'',b)}{\mathsf {w}}'\; \wedge \; {\mathsf {v}}\xrightarrow {\sigma ({\mathsf {v}})}{\mathsf {v}}_S\xrightarrow {(r''_{[y\leftarrow \gamma '(y)]},b)}{\mathsf {w}}\;\}\) Note that by definition of the set of edges of the game, \({\mathsf {w}}=({\mathsf {v}}_S,(r''_{[y\leftarrow \gamma '(y)]},b))\) and \({\mathsf {w}}'=({\mathsf {v}}'_S,(r'',b))\).
-
\({\mathsf {V}}_{\mathsf {def}} := {\mathsf {V}}_{\mathsf {def}} \cup \{{\mathsf {v}}'\}\)
-
-
-
For all \({\mathsf {v}}_D\in {\mathsf {V}}_D{\setminus } {\mathsf {V}}_{\mathsf {def}}\)
-
\(\sigma '({\mathsf {v}}_D) =\emptyset \)
-
Intuitively, the above algorithm is a search of \({\mathsf {Aut}(\sigma )}\). We propagate the encoding of the clocks of \(\sigma \) by clocks in \(\sigma '\) and iteratively build \(\sigma '\). The set \({\mathsf {Temp}}\) represents the triples to be processed and the set \({\mathsf {V}}_{\mathsf {def}}\) represents the states of Determinizator in the game for which the strategy \(\sigma '\) is defined. Moreover, the last step of the algorithm consists in arbitrarily defining the strategy for the unvisited states. By construction, these states are not reachable when Determinizator follows \(\sigma '\) hence this choice does not impact. Thus, \(\sigma '\) is well defined. The correction is a bit tedious, but intuitive: relations in the states in \(\sigma '\) give at least as much information as in \(\sigma \) because the time information of each clock \(x\) in \(\sigma \) is carried by \(\gamma (x)\) in the corresponding state in \(\sigma '\). The duplication of the information does not help to win.
Let us prove formally that \(\sigma '\) is a winning strategy using the following lemma.
Lemma 1
For all \(({\mathsf {v}}',{\mathsf {v}},\gamma ) \in {\mathsf {V}}_{\mathsf {def}}\) with \({\mathsf {v}}'=(\mathcal {E}_{{\mathsf {v}}'},(r',a'))\) and \({\mathsf {v}}=(\mathcal {E}_{{\mathsf {v}}},(r,a))\):
-
(i)
\(a'=a\)
-
(ii)
\(r=r'_{[y\leftarrow \gamma (y)]}\)
-
(iii)
\({\mathsf {v}}\) has no predecessor in \({\mathsf {Bad}}\)
-
(iv)
\(\forall {\mathsf {w}}'\) such that \(\exists ({\mathsf {v}}'_S,r'',b)\in {\mathsf {V}}_S\times {\mathsf {Act}}_S\) with \({\mathsf {v}}'\xrightarrow {\sigma '({\mathsf {v}}')}{\mathsf {v}}'_S\xrightarrow {(r'',b)}{\mathsf {w}}'\), then \(\exists ({\mathsf {w}}_0,\gamma _0)\in {\mathsf {V}}_D\times Y^Y\) such that \(({\mathsf {w}}',{\mathsf {w}}_0,\gamma _0)\in {\mathsf {V}}_{\mathsf {def}}\)
-
(v)
\(\mathcal {E}_{{\mathsf {v}}} \subseteq \{(\ell ,C'_{[y\leftarrow \gamma (y)]},\top )\;|\;(\ell ,C',\top )\in \mathcal {E}_{{\mathsf {v}}'}\} \cup \{(\ell ,C,\bot )\}\)
-
(vi)
\(\mathcal {E}_{{\mathsf {v}}'} \subseteq \{(\ell ,C',b')\;|\;(\ell ,C'_{[y\leftarrow \gamma (y)]},b)\in \mathcal {E}_{{\mathsf {v}}}\}\)
Let us first assume that this lemma is true. The fifth item implies that for all \(({\mathsf {v}}',{\mathsf {v}},\gamma )\in {\mathsf {V}}_{\mathsf {def}}\), \(({\mathsf {v}}\notin {\mathsf {Bad}}\Rightarrow {\mathsf {v}}'\notin {\mathsf {Bad}})\). The third item implies that the \({\mathsf {v}}'\)’s are not in \({\mathsf {Bad}}\). The fourth item implies that only these states \({\mathsf {v}}'\) (appearing in \({\mathsf {V}}_{\mathsf {def}}\)) impact on the fact that \(\sigma '\) is winning or not. As a consequence, if Lemma 1 is true, then \(\sigma '\) is winning.
Let us now prove Lemma 1.
Proof of Lemma 1
Items (i), (ii), (iii) are satisfied by triples initially added to \({\mathsf {Temp}}\). Moreover, the updates of \({\mathsf {Temp}}\) only add triples satisfying (i) and (ii) and whose a predecessor \({\mathsf {v}}_S\) of the second element is a state of Spoiler reachable following \(\sigma \), hence (iii) is satisfied too (only the configurations of \({\mathsf {v}}_S\) impact on whether \({\mathsf {v}}_S \in {\mathsf {Bad}}\) or not, and all the predecessors of \({\mathsf {v}}\) share the same set of configurations, by definition of \(\delta \)). Therefore, items (i), (ii), (iii) are satisfied for all triples of \({\mathsf {V}}_{\mathsf {def}}\).
Let us prove by induction that items (v) and (vi) are satisfied for all triples \(({\mathsf {v}}',{\mathsf {v}},\gamma )\in {\mathsf {V}}_{\mathsf {def}}\). Remark that all triples in \({\mathsf {V}}_{\mathsf {def}}\) are first added to \({\mathsf {Temp}}\). Triples initially added to \({\mathsf {Temp}}\) are such that \(\mathcal {E}_{{\mathsf {v}}}=\mathcal {E}_{{\mathsf {v}}'}\), hence they satisfy (v) and (vi). Let us prove now that if \(({\mathsf {v}}',{\mathsf {v}},\gamma )\in {\mathsf {V}}_{\mathsf {def}}\) satisfies (v) and (vi), then triples added to \({\mathsf {Temp}}\) during the inner loop for this triple, satisfy (v) and (vi) too. Let \(({\mathsf {w}}',{\mathsf {w}},\gamma ')\) with \({\mathsf {w}}'=(\mathcal {E}_{{\mathsf {w}}'},(r'',b))\) and \({\mathsf {w}}= (\mathcal {E}_{{\mathsf {w}}},(r''_{[y\leftarrow \gamma (y)]},b))\) be any triple added to \({\mathsf {Temp}}\) from \(({\mathsf {v}}',{\mathsf {v}},\gamma )\).
-
(v)
Let us first prove that \(\mathcal {E}_{{\mathsf {w}}} \subseteq \{(\ell ,C'_{[y\leftarrow \gamma '(y)]},\top )\;|\;(\ell ,C',\top )\in \mathcal {E}_{{\mathsf {w}}'}\} \cup \{(\ell ,C,\bot )\}\). For any \((\ell ,C,\top )\in \mathcal {E}_{{\mathsf {w}}}\), there exists \((\ell _0,C_0,\top )\in \mathcal {E}_{{\mathsf {v}}}\) such that by definition of the game:
-
\(\exists \ell _0 \xrightarrow {g,a,X'} \ell \in E\) s. t. \([r'_{[y\leftarrow \gamma (y)]}\cap C_0]_{|X} \cap g \ne \emptyset \)
-

-
\([r'_{[y\leftarrow \gamma (y)]}\cap C_0]_{|X} \subseteq g\)
By induction hypothesis, there exists \((\ell _0,C'_0,\top )\in \mathcal {E}_{v'}\) such that \({C'_0}_{[y\leftarrow \gamma (y)]}=C_0\), then:
-
\([r'_{[y\leftarrow \gamma (y)]}\cap {C'_0}_{[y\leftarrow \gamma (y)]}]_{|X} \cap g \ne \emptyset \)
-
\([r'_{[y\leftarrow \gamma (y)]}\cap {C'_0}_{[y\leftarrow \gamma (y)]}]_{|X} \subseteq g\)
This implies that:
-
\([r'\cap C'_0]_{|X} \cap g \ne \emptyset \)
-
\([r'\cap C'_0]_{|X} \subseteq g\)
Indeed, \([r'\cap C'_0]_{|X} \subseteq [r'_{|Im\gamma \cup X}\cap {C'_0}_{|Im\gamma \cup X}]_{|X} =[r'_{[y\leftarrow \gamma (y)]}\cap {C'_0}_{[y\leftarrow \gamma (y)]}]_{|X}\). Then \([r''\cap C'_0]_{|X} \cap g = \emptyset \) implies that \([r'\cap C'_0]_{|X} = \emptyset \) which is not possible if \(v'\) is a state of the game. As a consequence, there is a configuration \((\ell ,C',\top )\) in \(\mathcal {E}_{{\mathsf {w}}'}\) such that
 . Then:
. Then: 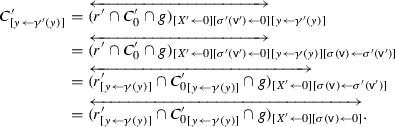
Therefore, \(({\mathsf {w}}',{\mathsf {w}},\gamma ')\) satisfies (v). Finally, all the triples in \({\mathsf {V}}_{\mathsf {def}}\) are added in \({\mathsf {Temp}}\) first, so that by induction \(v)\) is satisfied by all the triples in \({\mathsf {V}}_{\mathsf {def}}\).
-
-
(vi)
Let us now prove that \(\mathcal {E}_{{\mathsf {w}}'} \subseteq \{(\ell ,C',b')\;|\;(\ell ,C'_{[y\leftarrow \gamma (y)]},b)\in \mathcal {E}_{{\mathsf {w}}}\}\). For any \((\ell ,C',b')\in \mathcal {E}_{{\mathsf {w}}'}\), there exists \((\ell _0,C'_0,b)\in \mathcal {E}_{{\mathsf {v}}'}\) such that:
-
\(\exists \ell _0 \xrightarrow {g,a,X'} \ell \in E\) s. t. \([r'\cap C'_0]_{|X} \cap g \ne \emptyset \)
-

By induction hypothesis, there exists \((\ell _0,{C'_0}_{[y\leftarrow \gamma (y)]},b)\in \mathcal {E}_{{\mathsf {v}}}\), then:
-
\(\emptyset \ne [r'\cap C'_0]_{|X} \cap g \subseteq [r'_{[y\leftarrow \gamma (y)]}\cap {C'_0}_{[y\leftarrow \gamma (y)]}]_{|X} \cap g\)
As a consequence, there is a configuration \((\ell ,C,b)\) in \(\mathcal {E}_{{\mathsf {w}}}\) such that the relation
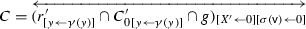 , which has been proved to be equal to \(C'_{[y\leftarrow \gamma '(y)]}\) above. Therefore \(vi)\) is satisfied by \(({\mathsf {w}}',{\mathsf {w}},\gamma ')\) and, by induction, by all the triples in \({\mathsf {V}}_{\mathsf {def}}\).
, which has been proved to be equal to \(C'_{[y\leftarrow \gamma '(y)]}\) above. Therefore \(vi)\) is satisfied by \(({\mathsf {w}}',{\mathsf {w}},\gamma ')\) and, by induction, by all the triples in \({\mathsf {V}}_{\mathsf {def}}\). -
Finally, let us prove that (iv) is also satisfied for all triples in \({\mathsf {V}}_{\mathsf {def}}\). Let \(({\mathsf {v}}',{\mathsf {v}},\gamma )\) be a triple in \({\mathsf {V}}_{\mathsf {def}}\). Let \({\mathsf {w}}'=(\mathcal {E}_{{\mathsf {w}}'},(r'',b))\) be a state of Determinizator such that \(\exists ({\mathsf {v}}'_S,r'',b)\in {\mathsf {V}}_S\times {\mathsf {Act}}_S\) such that \(({\mathsf {v}}',\sigma '({\mathsf {v}}'),{\mathsf {v}}'_S)\in \delta \;\wedge \;({\mathsf {v}}'_S,(r'',b),{\mathsf {w}}')\in \delta \). Then, there exists \((\ell _0,C'_0,b'_0)\in \mathcal {E}_{{\mathsf {w}}'}\) such that:
-
\(\exists \ell _0 \xrightarrow {g,b,X'} \ell '\in E\) s. t. \([r''\cap C'_0]_{|X} \cap g \ne \emptyset \)
Moreover, there exists \((\ell _1,C'_1,b'_1)\in \mathcal {E}_{{\mathsf {v}}'}\) such that:
-
\(\exists \ell _1 \xrightarrow {g_1,a,X'_1} \ell _0\in E\) s. t. \([r'\cap C'_1]_{|X} \cap g_1 \ne \emptyset \)
-
 .
.
As a consequence there exists a configuration \((\ell ,{C'_1}_{[y\leftarrow \gamma (y)]},b_1)\in \mathcal {E}_{v}\) such that:
-
\(\emptyset \ne [r'\cap C'_1]_{|X} \cap g_1 \subseteq [r'_{[y\leftarrow \gamma (y)]}\cap {C'_1}_{[y\leftarrow \gamma (y)]}]_{|X} \cap g_1\).
Then there exists a configuration \((\ell _0,C_0,b_0)\) of the successor \({\mathsf {v}}_S\) of \({\mathsf {v}}\) by the reset \(\sigma ({\mathsf {v}})\) such that:
If we define \(\gamma '\) as expected (\(\gamma '(y)= \gamma (y)\) if \(y \notin \sigma ({\mathsf {v}})\), \(\gamma '(y)= \sigma '({\mathsf {v}}')\) otherwise) then \(C_0={C'_0}_{[y\leftarrow \gamma '(y)]}\). Moreover, \(\emptyset \ne [r''\cap C'_0]_{|X} \cap g \subseteq [r''_{[y\leftarrow \gamma '(y)]}\cap {C'_0}_{[y\leftarrow \gamma '(y)]}]_{|X} \cap g\). Hence \((r''_{[y\leftarrow \gamma '(y)]},b)\) is a possible move of Spoiler from \({\mathsf {v}}_S\). Therefore there exists \({\mathsf {w}}\in {\mathsf {V}}_D\) such that \(({\mathsf {v}},\sigma ({\mathsf {v}}),{\mathsf {v}}_S)\in \delta \) and \(({\mathsf {v}}_S,(r''_{[y\leftarrow \gamma '(y)]},b),{\mathsf {w}})\in \delta \). As a consequence, the triple \(({\mathsf {w}}',{\mathsf {w}},\gamma ')\) is added to \({\mathsf {Temp}}\), then when this triple is taken from \({\mathsf {Temp}}\), either \(\sigma '({\mathsf {w}}')\) is not already defined and this triple is added to \({\mathsf {V}}_{\mathsf {def}}\), or \(\sigma '({\mathsf {w}}')\) has been already defined and another triple of the form \(({\mathsf {w}}',{\mathsf {w}}_0,\gamma _0)\) has been added in \({\mathsf {V}}_{\mathsf {def}}\). Therefore (iv) is satisfied by all triples \(({\mathsf {v}}',{\mathsf {v}},\gamma )\) in \({\mathsf {V}}_{\mathsf {def}}\). \(\square \)
Rights and permissions
About this article
Cite this article
Bertrand, N., Stainer, A., Jéron, T. et al. A game approach to determinize timed automata. Form Methods Syst Des 46, 42–80 (2015). https://doi.org/10.1007/s10703-014-0220-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10703-014-0220-1







 . Then:
. Then: 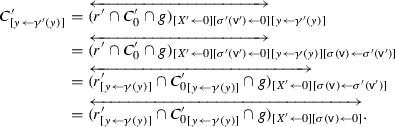

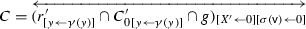 , which has been proved to be equal to
, which has been proved to be equal to  .
.