Abstract
In a recent work we have proposed a theoretical framework for developing optimized scheduling policies for complex resource allocation systems (RAS). This framework relies heavily on the expression of the RAS dynamics in the modeling framework of the Generalized Stochastic Petri Nets (GSPNs), and the employment of this GSPN-based representation towards the establishment of a systematic trade-off between the representational economy of the target scheduling policies and their operational efficiency. In this paper, we enhance the representational economy of the target policies in the aforementioned framework by taking advantage of some notions of “(non-)conflict” in the transitional dynamics of the underlying RAS-modeling GSPNs. A series of numerical experiments demonstrate that the representational gains resulting from the presented methodology can be very substantial.




Similar content being viewed by others
Notes
The key assumption behind this modeling practice is that the determination and communication of these resource allocation decisions requires a negligible time compared to the times that are involved in the execution of the various processing steps of the underlying system. Also, we notice that all the technical terms employed in this introductory discussion are fully defined in the more technical part of the paper.
A work in the past DES literature that has a similar flavor to the results that are presented herein, in that it tries to analyze the effects of some structural and behavioral properties of certain DES classes on their timed dynamics, is that of Glasserman and Yao (1994). Also, from a conceptual standpoint, the work presented in this paper has some affinity with the developments that are presented in Su and Wonham (2004), which seeks to establish representational economies for the supremal supervisor of DES that are modeled by finite state automata, through the identification and elimination of redundant information encoded in the original representation of this supervisor that is computed by the standard theory of Ramadge and Wonham (1989).
We remind the reader that T ∗ denotes the Kleene closure of the set T, i.e., all the finite-length strings consisting of elements from this set, including the empty string 𝜖.
In the case of RAS-modeling GSPNs, reversibility is ensured by (i) the assumption that the corresponding RAS starts its operation empty, and (ii) the role of the applied liveness-enforcing supervisor (LES), which ensures that every initiated process instance can run successfully to its completion.
The finiteness of \({\mathcal R}({\mathcal N})\), for any RAS-modeling GSPN \({\mathcal N}\), results from the finiteness of the various resource types of this RAS and the fact that each processing stage requires at least one resource unit for its execution.
The validity of this claim is easily established by some results in (static) network flow theory establishing the ability to distribute a unit of flow entering an acyclic connected digraph from a single source node to its terminal nodes in any possible manner, as long as the total amount of flow that is received by these nodes is equal to one.
On the other hand, it is also important to notice that Condition 1 cannot guarantee that the policy space \(\tilde {\Pi }^{S}(\delta )\) carries the performance potential of its counterpart policy space π S (δ). This limitation is due to the coupling that is introduced by Eq. 2 in the pricing of the random switches that correspond to distinct vanishing markings. Nevertheless, Condition 1 still guarantees that every CTMC \({\mathcal M}({\mathcal N})\) that is realizable in the original policy space π(δ), is also realizable by the policies in the policy space \(\tilde {\Pi }^{S}(\delta )\) through a controlled (partial) relaxation of the coupling that is defined by Eq. 2.
In lack of any bias that might result from special structure or further input, this can be the ordering that is defined by the natural indexing of the net transitions in T.
We remind the reader that this last quantity is defined as the size of any parsimonious encoding / representation of the septuple that defines GSPN \({\mathcal N}\).
A detailed treatment of the CRL scheduling problem through the methodological framework that is pursued by the considered research program can be found in Li and Reveliotis (2015b).
This assumption is in line with the standard timed semantics of the GSPN model, but more general distributions for the processing times involved can be approximated to any desired degree of accuracy through the methods of stages (Cassandras and Lafortune 2008).
In the case of processing stages with more general distributions for their processing times, the method of stages will substitute the corresponding timed transition with a Markovian subnet that will model the approximating “phase type” distribution.
c.f., for instance, the corresponding appendix in Ajmone Marsan et al. (1986), that introduced the GSPN model
We remind the reader that the technical meaning of this last statement is formalized in this paper through Definition 1 and its supporting discussion, and that, as far as we can tell, the content of this definition is a novel contribution of this work, especially when considered in the context of the GSPN modeling framework and its supporting theory.
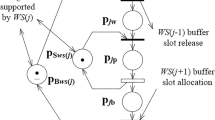
As revealed by the example digraph of Fig. 1b, the acyclic subspaces of \({\mathcal R}({\mathcal N})\) that interconnect each tangible marking m to its corresponding set of tangible markings \({\mathcal R}^{1}_{\mathcal T}(m)\), may involve a number of different paths connecting m with each element of \({\mathcal R}^{1}_{\mathcal T}(m)\), and each of these paths may involve a cascade of “decisions” modeled by the random switches of the corresponding vanishing markings. Hence, the actual number of the decision variables ξ for the scheduling problems that are formulated on the original policy space Π(δ) typically will be higher than the number of tangible markings that is provided in the second column of Table 3, sometimes by an order of magnitude.
References
Ajmone Marsan M, Balbo G, Conte G (1986) Performance Models of Multiprocessor Systems. The MIT Press, Cambridge
Ajmone Marsan M, Balbo G, Conte G, Donatelli S, Franceschinis G (1994) Modeling with Generalized Stochastic Petri Nets. John Wiley & Sons
Bertsekas DP (2012) Dynamic Programming and Optimal Control, 4th ed. Athena Scientific, Belmont
Cao X (2007) Stochastic Learning and Optimization. Springer, NY
Cassandras CG, Lafortune S (2008) Introduction to Discrete Event Systems, 2nd ed. Springer, NY
Giua A, DiCesare F, Silva M (1992) Generalized mutual exclusion constraints on nets with uncontrollable transitions. In: Proceedings of the 1992 IEEE Intl. Conference on Systems, Man and Cybernetics, pp 974–979. IEEE
Glasserman P, Yao D (1994) Monotone Structure in Discrete-Event Systems. John Wiley & Sons, Inc., NY
Iordache MV, Antsaklis PJ (2006) Supervisory Control of Concurrent Systems: A Petri net structural approach. Birkhäuser, Boston
Kumar PR (1994a) Scheduling manufacturing systems of re-entrant lines. In: Yao DD (ed) Stochastic Modeling and Analysis of Manufacturing Systems. Springer, pp 325–360
Kumar PR (1994b) Scheduling semiconductor manufacturing plants. IEEE Control Syst Mag 14–6:33–40
Kushner HJ, Yin GG (2003) Stochastic Approximation and Recursive Algorithms and Applications. Springer, NY
Li R, Reveliotis S (2015a) Performance optimization for a class of generalized stochastic Petri nets. Discrete Event Dynamic Systems: Theory and Applications 25:387–417
Li R, Reveliotis SA (2015b) Optimized scheduling of capacitated re-entrant lines. Technical Report (under development), Georgia Institute of Technology
Ramadge PJG, Wonham WM (1989) The control of discrete event systems. Proc IEEE 77:81–98
Reveliotis S (2015) Coordinating autonomy: Sequential resource allocation systems for automation. IEEE Robot Autom Mag 22:77–94
Reveliotis SA (2000) The destabilizing effect of blocking due to finite buffering capacity in multi-class queueing networks. IEEE Trans Autom Control 45:585–588
Reveliotis SA (2005) Real-time Management of Resource Allocation Systems: A Discrete Event Systems Approach. Springer, NY
Su R, Wonham WM (2004) Supervisor reduction for discrete-event systems. Discrete Event Dynamic Systems: Theory and Applications 14:31–53
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was partially supported by NSF grants CMMI-0928231 and ECCS-1405156.
Rights and permissions
About this article
Cite this article
Li, R., Reveliotis, S. Designing parsimonious scheduling policies for complex resource allocation systems through concurrency theory. Discrete Event Dyn Syst 26, 511–537 (2016). https://doi.org/10.1007/s10626-015-0219-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10626-015-0219-9