Abstract
FISTA is a popular convex optimisation algorithm which is known to converge at an optimal rate whenever a minimiser is contained in a suitable Hilbert space. We propose a modified algorithm where each iteration is performed in a subset which is allowed to change at every iteration. Sufficient conditions are provided for guaranteed convergence, although at a reduced rate depending on the conditioning of the specific problem. These conditions have a natural interpretation when a minimiser exists in an underlying Banach space. Typical examples are L1-penalised reconstructions where we provide detailed theoretical and numerical analysis.











Similar content being viewed by others
Data Availibility Statement
The synthetic STORM dataset was provided as part of the 2016 SMLM challenge, http://bigwww.epfl.ch/smlm/challenge2016/datasets/MT4.N2.HD/Data/data.html. The remaining examples used in this work can be generated with the supplementary code, https://github.com/robtovey/2020SpatiallyAdaptiveFISTA.
References
Alamo, T., Limon, D., Krupa, P.: Restart fista with global linear convergence. In: 2019 18th European Control Conference (ECC), pp. 1969–1974. IEEE (2019)
Aujol, J.F., Dossal, C.: Stability of over-relaxations for the forward-backward algorithm, application to fista. SIAM J. Optim. 25(4), 2408–2433 (2015)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2(1), 183–202 (2009)
Bonnefoy, A., Emiya, V., Ralaivola, L., Gribonval, R.: Dynamic screening: accelerating first-order algorithms for the lasso and group-lasso. IEEE Trans. Signal Process. 63(19), 5121–5132 (2015)
Boyd, N., Schiebinger, G., Recht, B.: The alternating descent conditional gradient method for sparse inverse problems. SIAM J. Optim. 27(2), 616–639 (2017)
Boyer, C., Chambolle, A., Castro, Y.D., Duval, V., De Gournay, F., Weiss, P.: On representer theorems and convex regularization. SIAM J. Optim. 29(2), 1260–1281 (2019)
Bredies, K., Pikkarainen, H.K.: Inverse problems in spaces of measures. ESAIM: Control, Optim. Calculus Var. 19(1), 190–218 (2013)
Castillo, I., Rockova, V.: Multiscale analysis of Bayesian CART. University of Chicago, Becker Friedman Institute for Economics Working Paper (2019-127) (2019)
Catala, P., Duval, V., Peyré, G.: A low-rank approach to off-the-grid sparse superresolution. SIAM J. Imag. Sci. 12(3), 1464–1500 (2019)
Chambolle, A., Dossal, C.: On the convergence of the iterates of the “fast iterative shrinkage/thresholding algorithm’’. J. Optim. Theory Appl. 166(3), 968–982 (2015)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imag. Vision 40(1), 120–145 (2011)
De Castro, Y., Gamboa, F., Henrion, D., Lasserre, J.B.: Exact solutions to super resolution on semi-algebraic domains in higher dimensions. IEEE Trans. Inf. Theory 63(1), 621–630 (2016)
Denoyelle, Q., Duval, V., Peyré, G., Soubies, E.: The sliding frank-wolfe algorithm and its application to super-resolution microscopy. Inverse Probl. 36(1), 014001 (2019)
Douglas, J., Rachford, H.H.: On the numerical solution of heat conduction problems in two and three space variables. Trans. Am. Math. Soc. 82(2), 421–439 (1956)
Duval, V., Peyré, G.: Sparse spikes super-resolution on thin grids i: the lasso. Inverse Probl. 33(5), 055008 (2017)
Duval, V., Peyré, G.: Sparse spikes super-resolution on thin grids ii: the continuous basis pursuit. Inverse Probl. 33(9), 095008 (2017)
Ekanadham, C., Tranchina, D., Simoncelli, E.P.: Recovery of sparse translation-invariant signals with continuous basis pursuit. IEEE Trans. Signal Process. 59(10), 4735–4744 (2011)
El Ghaoui, L., Viallon, V., Rabbani, T.: Safe feature elimination in sparse supervised learning. Tech. Rep. UCB/EECS-2010–126, EECS Department, University of California, Berkeley (2010)
Hiriart-Urruty, J.B., Lemaréchal, C.: Convex analysis and minimization algorithms II: advanced theory and bundle methods, vol. 305. Springer-Verlag, Berlin, Heidelberg (1993)
Huang, J., Sun, M., Ma, J., Chi, Y.: Super-resolution image reconstruction for high-density three-dimensional single-molecule microscopy. IEEE Trans. Comput. Imag. 3(4), 763–773 (2017)
Jiang, K., Sun, D., Toh, K.C.: An inexact accelerated proximal gradient method for large scale linearly constrained convex sdp. SIAM J. Optim. 22(3), 1042–1064 (2012)
Kekkonen, H., Lassas, M., Saksman, E., Siltanen, S.: Random tree besov priors–towards fractal imaging. http://arxiv.org/abs/2103.00574 (2021)
Liang, J., Fadili, J., Peyré, G.: Activity identification and local linear convergence of forward-backward-type methods. SIAM J. Optim. 27(1), 408–437 (2017)
Liang, J., Schönlieb, C.B.: Improving fista: Faster, smarter and greedier. http://arxiv.org/abs/1811.01430 (2018)
Ndiaye, E., Fercoq, O., Gramfort, A., Salmon, J.: Gap safe screening rules for sparsity enforcing penalties. J. Mach. Learn. Res. 18(1), 4671–4703 (2017)
Nesterov, Y.: Introductory lectures on convex optimization: a basic course. Kluwer Academic Publishers Boston, Dordrecht, London (2004)
Ovesnỳ, M., Křížek, P., Borkovec, J., Švindrych, Z., Hagen, G.M.: Thunderstorm: a comprehensive imageJ plug-in for palm and storm data analysis and super-resolution imaging. Bioinformatics 30(16), 2389–2390 (2014)
Parpas, P.: A multilevel proximal gradient algorithm for a class of composite optimization problems. SIAM J. Scientif. Comput. 39(5), S681–S701 (2017)
Poon, C., Keriven, N., Peyré, G.: The geometry of off-the-grid compressed sensing. Found Comput Math (2021)
Rosset, S., Zhu, J.: Piecewise linear regularized solution paths. Annals Stat. 87, 1012–1030 (2007)
Sage, D., Kirshner, H., Pengo, T., Stuurman, N., Min, J., Manley, S., Unser, M.: Quantitative evaluation of software packages for single-molecule localization microscopy. Nature Methods 12(8), 717–724 (2015)
Sage, D., Pham, T.A., Babcock, H., Lukes, T., Pengo, T., Chao, J., Velmurugan, R., Herbert, A., Agrawal, A., Colabrese, S., et al.: Super-resolution fight club: assessment of 2d and 3d single-molecule localization microscopy software. Nature Methods 16(5), 387–395 (2019)
Schermelleh, L., Ferrand, A., Huser, T., Eggeling, C., Sauer, M., Biehlmaier, O., Drummen, G.P.: Super-resolution microscopy demystified. Nature Cell Biol. 21(1), 72–84 (2019)
Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., Preibisch, S., Rueden, C., Saalfeld, S., Schmid, B., et al.: Fiji: an open-source platform for biological-image analysis. Nature Methods 9(7), 676–682 (2012)
Schmidt, M., Roux, N.L., Bach, F.R.: Convergence rates of inexact proximal-gradient methods for convex optimization. In: Advances in Neural Information Processing Systems, pp. 1458–1466 (2011)
Strang, G.: Approximation in the finite element method. Numerische Mathematik 19(1), 81–98 (1972)
Tao, S., Boley, D., Zhang, S.: Local linear convergence of ista and fista on the lasso problem. SIAM J. Optim. 26(1), 313–336 (2016)
Unser, M., Fageot, J., Gupta, H.: Representer theorems for sparsity-promoting \(\ell ^1\) regularization. IEEE Trans. Inf. Theory 62(9), 5167–5180 (2016)
Villa, S., Salzo, S., Baldassarre, L., Verri, A.: Accelerated and inexact forward-backward algorithms. SIAM J. Optim. 23(3), 1607–1633 (2013)
Yu, J., Lai, R., Li, W., Osher, S.: A fast proximal gradient method and convergence analysis for dynamic mean field planning. http://arxiv.org/abs/2102.13260 (2021)
Acknowledgements
R.T. acknowledges funding from EPSRC grant EP/L016516/1 for the Cambridge Centre for Analysis, and the ANR CIPRESSI project grant ANR-19-CE48-0017-01 of the French Agence Nationale de la Recherche. Most of this work was done while A.C. was still in CMAP, CNRS and Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France. Both authors would like to thank the anonymous reviewers who put in so much effort to improving this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors have no conflicts of interest to declare which are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Proofs for FISTA convergence
This section contains all of the statements and proofs of the results contained in Sect. 4. Recall that the subsets \(\mathbb {U}^n\subset \mathbb {H}\) satisfy (10).
1.1 A.1 Proofs for Step 3
Theorem 5
(Lemma 2) Let  be chosen arbitrarily and
be chosen arbitrarily and  /
/ be generated by Algorithm 1 for all \(n\in \mathbb {N}\). For all \(n>0\), it holds that
be generated by Algorithm 1 for all \(n\in \mathbb {N}\). For all \(n>0\), it holds that

Proof
Modifying [10, Thm 3.2], for \(n\ge 1\) we apply Lemma 1 with  and
and  . By (10),
. By (10),  is convex so
is convex so  . This gives
. This gives

By the convexity of \({\text {E}}\), this reduces to

Multiplying through by \(t_n^2\) gives the desired inequality. \(\square \)
Theorem 6
(Theorem 1) Fix a sequence of subsets \((\mathbb {U}^n)_{n\in \mathbb {N}}\) satisfying (10), arbitrary  , and FISTA stepsize choice \((t_n)_{n\in \mathbb {N}}\). Let
, and FISTA stepsize choice \((t_n)_{n\in \mathbb {N}}\). Let  and
and  be generated by Algorithm 1, then, for any choice of
be generated by Algorithm 1, then, for any choice of  and \(N\in \mathbb {N}\) we have
and \(N\in \mathbb {N}\) we have

Proof
Theorem 6 is just a summation of (74) over all \(n=1,\ldots ,N\). To see this: first add and subtract  to each term on the left-hand side to convert \({\text {E}}\) to \({\text {E}}_0\), then move
to each term on the left-hand side to convert \({\text {E}}\) to \({\text {E}}_0\), then move  to the right-hand side. Now (74) becomes
to the right-hand side. Now (74) becomes

Summing this inequality from \(n=1\) to \(n=N\) gives

The final step is to flip the roles of  /
/ in the final inner product term. Re-writing the right-hand side gives
in the final inner product term. Re-writing the right-hand side gives

Noting that  , the previous two equations combine to prove the statement of Theorem 6. \(\square \)
, the previous two equations combine to prove the statement of Theorem 6. \(\square \)
The following lemma is used to produce a sharper estimate on sequences \(t_n\).
Lemma 10
If \(\rho _n=t_{n}^2-t_{n+1}^2+t_{n+1}\ge 0\), \(t_n\ge 1\) for all \(n\in \mathbb {N}\) then \(t_n\le n-1 +t_1\).
Proof
This is trivially true for \(n=1\). Suppose true for \(n-1\), the condition on \(\rho _{n-1}\) gives
Assuming the contradiction, if \(t_n> n-1+t_1\) then the above equation simplifies to \(n-1+t_1 < 1\). However, \(t_1\ge 1\) implying that \(n<1\) which completes the contradiction. \(\square \)
Lemma 11
(Lemma 3) Let  ,
,  be generated by Algorithm 1 with \((\mathbb {U}^n)_{n\in \mathbb {N}}\) satisfying (10), \((n_k\in \mathbb {N})_{k\in \mathbb {N}}\) be a monotone increasing sequence, and choose
be generated by Algorithm 1 with \((\mathbb {U}^n)_{n\in \mathbb {N}}\) satisfying (10), \((n_k\in \mathbb {N})_{k\in \mathbb {N}}\) be a monotone increasing sequence, and choose

for each \(k\in \mathbb {N}\). If such a sequence exists, then for all \(K\in \mathbb {N}\), \(n_K\le N<n_{K+1}\) we have

where  .
.
Proof
This is just a telescoping of the right-hand side of (77) with the introduction of \(n_k\) and simplification  ,
,

By Lemma 10, \(t_n\le n\) so we can further simplify

to get the required bound. \(\square \)
1.2 A.2 Proof for Step 4
Lemma 12
(Lemma 4) Suppose  and \(n_k\) satisfy the conditions of Lemma 3 and
and \(n_k\) satisfy the conditions of Lemma 3 and  forms an
forms an
\((a_{{\text {U}}},a_{{\text {E}}})\)-minimising sequence of \({\text {E}}\) with

If either:
-
\(a_{{\text {U}}}>1\) and \(n_k^2\lesssim a_{{\text {E}}}^ka_{{\text {U}}}^{2k}\),
-
or \(a_{{\text {U}}}=1\), \(\sum _{k=1}^\infty n_k^2a_{{\text {E}}}^{-k}<\infty \), and
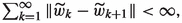
then

Proof
Starting from Lemma 11 we have


The inductive step now depends on the value of \(a_{{\text {U}}}\).
-
Case \(a_{{\text {U}}}>1\): We simplify the inequality
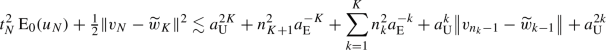 (86)
(86) (87)
(87)for some \(C_1>C\). Choose
 such that $$\begin{aligned} \frac{1}{2}C_2^2 \ge \frac{C_1}{a_{{\text {U}}}^2-1}(C_2+a_{{\text {U}}}^2). \end{aligned}$$(88)
such that $$\begin{aligned} \frac{1}{2}C_2^2 \ge \frac{C_1}{a_{{\text {U}}}^2-1}(C_2+a_{{\text {U}}}^2). \end{aligned}$$(88)Assume
 for \(1\le k\le K\) (trivially true for \(K=1\)), then for \(N=n_{K+1}-1\) we have
for \(1\le k\le K\) (trivially true for \(K=1\)), then for \(N=n_{K+1}-1\) we have  (89)
(89) (90)
(90) (91)
(91) -
Case \(a_{{\text {U}}}=1\): Denote
 and note that
and note that  . We therefore bound
. We therefore bound 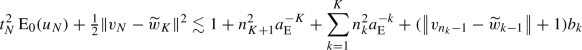 (92)
(92) (93)
(93)for some \(C_1>0\). Choose
 such that
such that 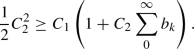 (94)
(94)Assume
 for \(1\le k\le K\) (trivially true for \(K=1\)), then for \(N=n_{K+1}-1\) we have
for \(1\le k\le K\) (trivially true for \(K=1\)), then for \(N=n_{K+1}-1\) we have  (95)
(95)
In both cases, the induction on  holds for all K, and we have
holds for all K, and we have  for all \(N<n_K-1\). \(\square \)
for all \(N<n_K-1\). \(\square \)
1.3 A.3 Proof for Step 5
Lemma 13
(Lemma 5) Suppose  and \(n_k\) are sequences satisfying
and \(n_k\) are sequences satisfying

then

Proof
The proof is direct computation, note that
therefore
so  as required. \(\square \)
as required. \(\square \)
1.4 A.4 Proofs for Step 6
Theorem 7
(Theorem 3) Let \((\mathbb {U}^n\subset \mathbb {H})_{n\in \mathbb {N}}\) be a sequence of subsets satisfying (10), compute  and
and  by Algorithm 1. Suppose that there exists a monotone increasing sequence \(n_k\in \mathbb {N}\) such that
by Algorithm 1. Suppose that there exists a monotone increasing sequence \(n_k\in \mathbb {N}\) such that

for all \(k\in \mathbb {N}\).
If  is an \((a_{{\text {U}}},a_{{\text {E}}})\)-minimising sequence of \({\text {E}}\) with \(a_{{\text {U}}}>1\) and \(n_k^2\lesssim a_{{\text {E}}}^ka_{{\text {U}}}^{2k}\), then
is an \((a_{{\text {U}}},a_{{\text {E}}})\)-minimising sequence of \({\text {E}}\) with \(a_{{\text {U}}}>1\) and \(n_k^2\lesssim a_{{\text {E}}}^ka_{{\text {U}}}^{2k}\), then

uniformly for \(N\in \mathbb {N}\).
Proof
Let \(C>0\) satisfy \(n_k^2\le Ca_{{\text {E}}}^ka_{{\text {U}}}^{2k}\) for each \(k\in \mathbb {N}\). Fix \(N>C\) and choose k such that \(Ca_{{\text {E}}}^{k-1}a_{{\text {U}}}^{2k-2}\le N<Ca_{{\text {E}}}^ka_{{\text {U}}}^{2k}\). By construction, and using the equality from (96), we have

as required. \(\square \)
Lemma 14
(Lemma 6) Let  be a sequence in \(\mathbb {H}\) with
be a sequence in \(\mathbb {H}\) with  . Suppose
. Suppose  and denote
and denote  . Any of the following conditions are sufficient to show that
. Any of the following conditions are sufficient to show that  is an \((a_{{\text {U}}},a_{{\text {E}}})\)-minimising sequence of \({\text {E}}\):
is an \((a_{{\text {U}}},a_{{\text {E}}})\)-minimising sequence of \({\text {E}}\):
-
1.
Small continuous gap refinement:
 for all \(k\in \mathbb {N}\), some
for all \(k\in \mathbb {N}\), some  .
. -
2.
Small discrete gap refinement:
 and
and  for all \(k>0\), some
for all \(k>0\), some  .
.
Otherwise, suppose there exists a Banach space  which contains each \(\widetilde{\mathbb {U}}^k\),
which contains each \(\widetilde{\mathbb {U}}^k\),  , and the sublevel sets of \({\text {E}}\) are
, and the sublevel sets of \({\text {E}}\) are  -bounded. With the subdifferential \(\partial {\text {E}}:\mathbb {U}\rightrightarrows \mathbb {U}^*\), it is also sufficient if either:
-bounded. With the subdifferential \(\partial {\text {E}}:\mathbb {U}\rightrightarrows \mathbb {U}^*\), it is also sufficient if either:
-
3.
Small continuous gradient refinement:
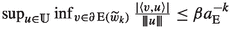 for all \(k\in \mathbb {N}\), some
for all \(k\in \mathbb {N}\), some 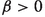 .
. -
4.
Small discrete gradient refinement:
 and
and  for all \(k\in \mathbb {N}\), some
for all \(k\in \mathbb {N}\), some  , where
, where  .
.
Proof
The conditions for \(a_{{\text {U}}}\) in Definition 1 are already met, it remains to be shown that  for some fixed \(C>0\). For cases (3) and (4), fix \(R>0\) such that both
for some fixed \(C>0\). For cases (3) and (4), fix \(R>0\) such that both  and the sublevel set
and the sublevel set  are contained in the ball of radius R. Any minimising sequences of \({\text {E}}\) in \(\mathbb {U}\) or \(\widetilde{\mathbb {U}}^k\) are contained in this ball. We can therefore compute C in each case:
are contained in the ball of radius R. Any minimising sequences of \({\text {E}}\) in \(\mathbb {U}\) or \(\widetilde{\mathbb {U}}^k\) are contained in this ball. We can therefore compute C in each case:
-
(1)
 , so
, so  suffices.
suffices. -
(2)
 , so \(C=(a_{{\text {E}}}+1)\beta \) suffices.
, so \(C=(a_{{\text {E}}}+1)\beta \) suffices. -
(3)
 for any
for any 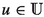 with
with  . Maximising over
. Maximising over  gives
gives 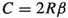
-
(4)
 for any
for any  with
with  , so
, so  and
and  .
.
This completes the requirements of Definition 1. \(\square \)
B Proof of Theorem 4
First we recall the setting of Definition 2, fix: \(p\ge 0\), \(q\in [1,\infty ]\), \(h\in (0,1)\), \(N\in \mathbb {N}\), connected and bounded domain \(\varOmega \subset \mathbb {R}^d\), and  . We assume that \(\mathbb {H}=L^2(\varOmega )\),
. We assume that \(\mathbb {H}=L^2(\varOmega )\),  , and there exist spaces \((\widetilde{\mathbb {U}}^k)_{k\in \mathbb {N}}\) with \(\widetilde{\mathbb {U}}^k\subset \mathbb {U}\) containing a sequence
, and there exist spaces \((\widetilde{\mathbb {U}}^k)_{k\in \mathbb {N}}\) with \(\widetilde{\mathbb {U}}^k\subset \mathbb {U}\) containing a sequence  such that
such that  , c.f. (16). Furthermore, there exists constant \(c_\alpha >0\) and meshes \(\mathbb {M}^k\) such that:
, c.f. (16). Furthermore, there exists constant \(c_\alpha >0\) and meshes \(\mathbb {M}^k\) such that:


In this section, these assumptions will be summarised simply by saying that \(\mathbb {H}\) and \((\widetilde{\mathbb {U}}^k)_{k\in \mathbb {N}}\) satisfy Definition 2. We prove Theorem 4 as a consequence of Lemma 7, namely we compute exponents \(p',q'\) with \(a_{{\text {U}}}=h^{-q'}\) and \(a_{{\text {E}}}=h^{-p'}\). These values are computed as the result of the following three lemmas. The first, Lemma 15, is a quantification of the equivalence between \(L^q\) and \(L^2\) norms on general sub-spaces. Lemma 16 applies this result to finite-element spaces to compute the value of \(q'\). Finally, Lemma 17 then performs the computations for \(p'\) depending on the smoothness properties of \({\text {E}}\).
Lemma 15
(Equivalence of norms for fixed k) Suppose \(\mathbb {H}= L^2(\varOmega )\) for some connected, bounded domain \(\varOmega \subset \mathbb {R}^d\) and  for some \(q\in [1,\infty ]\), \(C>0\). For any linear subspace \(\widetilde{\mathbb {U}}\subset \mathbb {U}\) and
for some \(q\in [1,\infty ]\), \(C>0\). For any linear subspace \(\widetilde{\mathbb {U}}\subset \mathbb {U}\) and  ,
,

Proof
The first statement of the result is by definition, for each  we have
we have

Recall  . To go further we use Hölder’s inequality. If \(\frac{1}{q}+\frac{1}{q^*}=1\), then for any
. To go further we use Hölder’s inequality. If \(\frac{1}{q}+\frac{1}{q^*}=1\), then for any 

If \(q\ge 2\) we use Hölder’s inequality a second time:

This confirms the inequality when \(q\ge 2\). If \(q<2\), we can simply upper bound \({\left\Vert \cdot \right\Vert }_{q^*}\le |\varOmega |^{\frac{1}{q^*}}{\left\Vert \cdot \right\Vert }_\infty \) as required. \(\square \)
Lemma 16
Suppose \(\mathbb {H}\) and \((\widetilde{\mathbb {U}}^k)_{k\in \mathbb {N}}\) satisfy Definition 2, then
-
1.
If \(q\ge 2\), then
 (i.e. \(q'=0\)).
(i.e. \(q'=0\)). -
2.
If \(q<2\) and
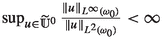 , then
, then  (i.e. \(q'=-\frac{d}{2}\)).
(i.e. \(q'=-\frac{d}{2}\)).
Proof
Most of the conditions of Lemma 15 are already satisfied. Furthermore observe that  . For the \(q\ge 2\) case, this is already sufficient to conclude
. For the \(q\ge 2\) case, this is already sufficient to conclude  from Lemma 15, as required.
from Lemma 15, as required.
For the case \(q<2\), from Lemma 15 recall that we are required to bound

However, due to the decomposition property (100), for each \(\omega \in \mathbb {M}^k\) and  there exists
there exists  such that
such that

Combining these two equations with the assumed bound on  confirms
confirms  as required. \(\square \)
as required. \(\square \)
Lemma 17
Suppose \(\mathbb {H}\) and \((\widetilde{\mathbb {U}}^k)_{k\in \mathbb {N}}\) satisfy Definition 2 and  is the minimiser of E such that
is the minimiser of E such that  .
.
-
1.
If \({\text {E}}\) is
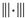 -Lipschitz at
-Lipschitz at  , then
, then  (i.e. \(p'=p\)).
(i.e. \(p'=p\)). -
2.
If \(\nabla {\text {E}}\) is
 -Lipschitz at
-Lipschitz at  , then
, then  (i.e. \(p'=2p\)).
(i.e. \(p'=2p\)).
Proof
Both statements are direct by definition, observe


The proof is concluded by using the approximation bounds of  in Definition 2. \(\square \)
in Definition 2. \(\square \)
Operator norms for numerical examples
Theorem 8
Suppose \(\textsf{A}:\mathbb {H} \rightarrow \mathbb {R}^m\) has kernels \(\psi _j\in L^\infty ([0,1]^d)\) for \(j\in [m]\).
-
Case 1:
If \(\psi _j(\vec {x}) = {\left\{ \begin{array}{ll} 1 &{} \vec {x}\in \mathbb {X}_j \\ 0 &{} \text { else}\end{array}\right. }\) for some collection \(\mathbb {X}_j\subset \varOmega \) such that \(\mathbb {X}_i\cap \mathbb {X}_j = \emptyset \) for all \(i\ne j\), then \({\left\Vert \textsf{A} \right\Vert }_{L^2\rightarrow \ell ^2} = \max _{j\in [m]} \sqrt{|\mathbb {X}_j|}.\)
-
Case 2:
If
 for some frequencies
for some frequencies  with
with  , then $$\begin{aligned} {\left\Vert \textsf{A} \right\Vert }_{L^2\rightarrow \ell ^2} \le \sqrt{m}, \qquad |\textsf{A}^*\vec {r}|_{C^k}\le m^{1-\frac{1}{q}}A^k{\left\Vert \vec {r} \right\Vert }_q, \quad \text {and}\quad |\textsf{A}^*|_{\ell ^2\rightarrow C^k}\le \sqrt{m}A^k \end{aligned}$$
, then $$\begin{aligned} {\left\Vert \textsf{A} \right\Vert }_{L^2\rightarrow \ell ^2} \le \sqrt{m}, \qquad |\textsf{A}^*\vec {r}|_{C^k}\le m^{1-\frac{1}{q}}A^k{\left\Vert \vec {r} \right\Vert }_q, \quad \text {and}\quad |\textsf{A}^*|_{\ell ^2\rightarrow C^k}\le \sqrt{m}A^k \end{aligned}$$for all \(\vec {r}\in \mathbb {R}^m\) and \(q\in [1,\infty ]\).
-
Case 3:
Suppose \(\psi _j(\vec {x}) = (2\pi \sigma ^2)^{-\frac{d}{2}}\exp \left( -\frac{|\vec {x}-\vec {x}_j|^2}{2\sigma ^2}\right) \) for some regular mesh \(\vec {x}_j\in [0,1]^d\) and separation \(\varDelta \). i.e.
$$\begin{aligned} \{\vec {x}_j{{\,\mathrm{\;s.t.\;}\,}}j\in [m]\} = \{\vec {x}_0 + (j_1\varDelta ,\ldots ,j_d\varDelta ){{\,\mathrm{\;s.t.\;}\,}}j_i\in [\widehat{m}]\} \end{aligned}$$for some \(\vec {x}_0\in \mathbb {R}^d\), \(\widehat{m}{:}{=}\root d \of {m}\). For all \(\frac{1}{q} + \frac{1}{q^*} = 1\), \(q\in (1,\infty ]\), we have
$$\begin{aligned} {\left\Vert \textsf{A} \right\Vert }_{L^2\rightarrow \ell ^2}&\le \bigg ((4\pi \sigma ^2)^{-\frac{1}{2}}\sum _{j=-2\widehat{m},\ldots ,2\widehat{m}}\exp (-\tfrac{\varDelta ^2}{4\sigma ^2}j^2)\bigg )^d, \end{aligned}$$(108)$$\begin{aligned} |\textsf{A}^*\vec {r}|_{C^0}&\le (2\pi \sigma ^2)^{-\frac{d}{2}}\bigg (\sum _{\vec j\in J}\exp \left( -\tfrac{q^*\varDelta ^2}{2\sigma ^2}\max (0,|\vec j|-\delta )^2\right) \bigg )^{\frac{1}{q^*}}{\left\Vert \vec {r} \right\Vert }_q, \end{aligned}$$(109)$$\begin{aligned} |\textsf{A}^*\vec {r}|_{C^1}&\le \frac{(2\pi \sigma ^2)^{-\frac{d}{2}}}{\sigma }\frac{\varDelta }{\sigma }\bigg (\sum _{\vec j\in J}(|\vec j|+\delta )^{q^*}\exp \left( -\tfrac{q^*\varDelta ^2}{2\sigma ^2}\max (0,|\vec j|-\delta )^2\right) \bigg )^{\frac{1}{q^*}}{\left\Vert \vec {r} \right\Vert }_q, \end{aligned}$$(110)$$\begin{aligned} |\textsf{A}^*\vec {r}|_{C^2}&\le \frac{(2\pi \sigma ^2)^{-\frac{d}{2}}}{\sigma ^2} \bigg (\sum _{\vec j\in J} \left( 1+\tfrac{\varDelta ^2}{\sigma ^2}(|\vec j|+\delta )^2\right) ^{q^*}\nonumber \\&\qquad \exp \left( -\tfrac{q^*\varDelta ^2}{2\sigma ^2}\max (0,|\vec j|-\delta )^2\right) \bigg )^{\frac{1}{q^*}} {\left\Vert \vec {r} \right\Vert }_q, \end{aligned}$$(111)where \(\delta = \frac{\sqrt{d}}{2}\) and \(J=\{\vec j\in \mathbb {Z}^d {{\,\mathrm{\;s.t.\;}\,}}{\left\Vert \vec j \right\Vert }_{\ell ^\infty }\le 2\widehat{m}\}\). The case for \(q=1\) can be inferred from the standard limit of \({\left\Vert \cdot \right\Vert }_{{q^*}}\rightarrow {\left\Vert \cdot \right\Vert }_{\infty }\) for \(q^*\rightarrow \infty \).
Proof
(Case 1.) From Lemma 8 we have
Therefore, \(\textsf{A}\textsf{A}^*\) is a diagonal matrix and \({\left\Vert \textsf{A}\textsf{A}^* \right\Vert }_{\ell ^2\rightarrow \ell ^2} = \max _{j\in [m]} |\mathbb {X}_j|\) completes the result. \(\square \)
Proof
(Case 2.) \(\psi _j\) are not necessarily orthogonal however \(|\left\langle \psi _i,\psi _j \right\rangle |\le 1\) therefore we can estimate
Now looking to apply Lemma 9, note \({\left\Vert \nabla ^k\psi _j \right\Vert }_\infty \le A^k\), therefore
\(\square \)
Proof
(Case 3.) In the Gaussian case, we build our approximations around the idea that sums of Gaussians should converge very quickly. The first example can be used to approximate the operator norm. Computing the inner products gives
Estimating the operator norm,
This is a nice approximation because it factorises simply over dimensions. Applying the results from Lemma 9, note
We now wish to sum over \(j=1,\ldots ,m\) and produce an upper bound on these, independent of t. To do so we will use the following lemma.
Lemma 18
Suppose \(q>0\). If the polynomial \(p(|\vec {x}|) = \sum p_k|\vec {x}|^k\) has non-negative coefficients and \(\vec {x}\in [-m,m]^d\), then
where \(\delta {:}{=}\frac{\sqrt{d}}{2}\) and \(\vec {j}\in \mathbb {Z}^d\).
Proof
There exists \(\widehat{\vec {x}}\in [-\tfrac{1}{2},\tfrac{1}{2}]^d\) such that \(\vec {x} + \widehat{\vec {x}}\in \mathbb {Z}^d\), therefore
as \(|\widehat{\vec {x}}|\le \delta \) and p has non-negative coefficients. \(\square \)
Now, continuing the proof of Theorem 8, for \(\widehat{m}=\root d \of {m}\), \(\delta =\frac{\sqrt{d}}{2}\) and \(J=\{\vec {j}\in \mathbb {Z}^d {{\,\mathrm{\;s.t.\;}\,}}{\left\Vert \vec {j} \right\Vert }_{\ell ^\infty }\le 2\widehat{m}\}\), Lemma 18 bounds
for all \(\vec {x}\in \varOmega \). In a worst case, this is \(O(2^dm)\) time complexity however the summands all decay faster than exponentially and so should converge very quickly. \(\square \)
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chambolle, A., Tovey, R. “FISTA” in Banach spaces with adaptive discretisations. Comput Optim Appl 83, 845–892 (2022). https://doi.org/10.1007/s10589-022-00418-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-022-00418-3



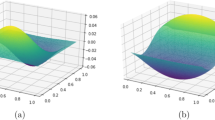

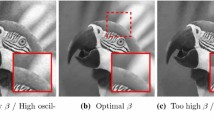
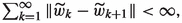
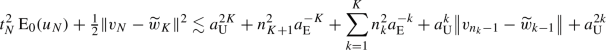

 such that
such that  for
for 


 and note that
and note that  . We therefore bound
. We therefore bound 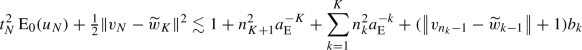

 such that
such that 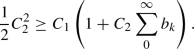
 for
for 
 for all
for all  .
. and
and  for all
for all  .
.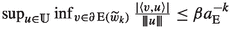 for all
for all 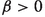 .
. and
and  for all
for all  , where
, where  .
. , so
, so  suffices.
suffices. , so
, so  for any
for any 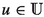 with
with  . Maximising over
. Maximising over  gives
gives 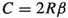
 for any
for any  with
with  , so
, so  and
and  .
. (i.e.
(i.e. 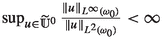 , then
, then  (i.e.
(i.e.  -Lipschitz at
-Lipschitz at  , then
, then  (i.e.
(i.e.  -Lipschitz at
-Lipschitz at  , then
, then  (i.e.
(i.e.  for some frequencies
for some frequencies  with
with  , then
, then