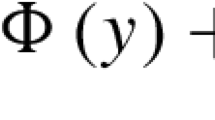Abstract
We develop two new proximal alternating penalty algorithms to solve a wide range class of constrained convex optimization problems. Our approach mainly relies on a novel combination of the classical quadratic penalty, alternating minimization, Nesterov’s acceleration, adaptive strategy for parameters. The first algorithm is designed to solve generic and possibly nonsmooth constrained convex problems without requiring any Lipschitz gradient continuity or strong convexity, while achieving the best-known \(\mathcal {O}\left( \frac{1}{k}\right) \)-convergence rate in a non-ergodic sense, where k is the iteration counter. The second algorithm is also designed to solve non-strongly convex, but semi-strongly convex problems. This algorithm can achieve the best-known \(\mathcal {O}\left( \frac{1}{k^2}\right) \)-convergence rate on the primal constrained problem. Such a rate is obtained in two cases: (1) averaging only on the iterate sequence of the strongly convex term, or (2) using two proximal operators of this term without averaging. In both algorithms, we allow one to linearize the second subproblem to use the proximal operator of the corresponding objective term. Then, we customize our methods to solve different convex problems, and lead to new variants. As a byproduct, these algorithms preserve the same convergence guarantees as in our main algorithms. We verify our theoretical development via different numerical examples and compare our methods with some existing state-of-the-art algorithms.







Similar content being viewed by others
Notes
A recent work in [1] showed an \({o}\left( \frac{1}{k}\right) \) or \({o}\left( \frac{1}{k^2}\right) \) rate depending on problem structures.
References
Attouch, H., Chbani, Z., Riahi, H.: Rate of convergence of the Nesterov accelerated gradient method in the subcritical case \(\alpha \le 3\). ESAIM: COCV (2017). https://doi.org/10.1051/cocv/2017083
Auslender, A., Teboulle, M.: Interior gradient and proximal methods for convex and conic optimization. SIAM J. Optim. 16(3), 697–725 (2006)
Bauschke, H.H., Combettes, P.: Convex Analysis and Monotone Operators Theory in Hilbert Spaces, 2nd edn. Springer, Berlin (2017)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding agorithm for linear inverse problems. SIAM J. Imaging Sci. 2(1), 183–202 (2009)
Becker, S., Candès, E.J., Grant, M.: Templates for convex cone problems with applications to sparse signal recovery. Math. Program. Comput. 3(3), 165–218 (2011)
Belloni, A., Chernozhukov, V., Wang, L.: Square-root LASSO: pivotal recovery of sparse signals via conic programming. Biometrika 94(4), 791–806 (2011)
Ben-Tal, A., Nemirovski, A.: Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications, Volume 3 of MPS/SIAM Series on Optimization. SIAM, Philadelphia (2001)
Bertsekas, D.P.: Nonlinear Programming, 2nd edn. Athena Scientific, Nashua (1999)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011)
Boyd, S., Vandenberghe, L.: Convex Optimization. University Press, Cambridge (2004)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)
Chambolle, A., Pock, T.: On the ergodic convergence rates of a first-order primal–dual algorithm. Math. Program. 159(1–2), 253–287 (2016)
Chen, G., Teboulle, M.: A proximal-based decomposition method for convex minimization problems. Math. Program. 64, 81–101 (1994)
Condat, L.: A primal–dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158, 460–479 (2013)
Davis, D.: Convergence rate analysis of primal–dual splitting schemes. SIAM J. Optim. 25(3), 1912–1943 (2015)
Davis, D.: Convergence rate analysis of the forward-Douglas–Rachford splitting scheme. SIAM J. Optim. 25(3), 1760–1786 (2015)
Davis, D., Yin, W.: Faster convergence rates of relaxed Peaceman–Rachford and ADMM under regularity assumptions. Math. Oper. Res. 42, 783–805 (2014)
Du, Y., Lin, X., Ruszczyński, A.: A selective linearization method for multiblock convex optimization. SIAM J. Optim. 27(2), 1102–1117 (2017)
Eckstein, J., Bertsekas, D.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 55, 293–318 (1992)
Esser, E., Zhang, X., Chan, T.: A general framework for a class of first order primal-dual algorithms for TV-minimization. SIAM J. Imaging Sci. 3(4), 1015–1046 (2010)
Fletcher, R.: Practical Methods of Optimization, 2nd edn. Wiley, Chichester (1987)
Goldfarb, D., Ma, S., Scheinberg, K.: Fast alternating linearization methods of minimization of the sum of two convex functions. Math. Program. Ser. A 141(1), 349–382 (2012)
Goldstein, T., O’Donoghue, B., Setzer, S.: Fast alternating direction optimization methods. SIAM J. Imaging Sci. 7(3), 1588–1623 (2012)
Grant, M., Boyd, S., Ye, Y.: Disciplined convex programming. In: Liberti, L., Maculan, N. (eds.) Global Optimization: From Theory to Implementation, Nonconvex Optimization and Its Applications, pp. 155–210. Springer, Berlin (2006)
He, B.S., Yuan, X.M.: On the \({O}(1/n)\) convergence rate of the Douglas–Rachford alternating direction method. SIAM J. Numer. Anal. 50, 700–709 (2012)
Jaggi, M.: Revisiting Frank–Wolfe: projection-free sparse convex optimization. JMLR W&CP 28(1), 427–435 (2013)
Johnson, R., Zhang, T.: Accelerating stochastic gradient descent using predictive variance reduction. In: Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q. (eds.), Advances in Neural Information Processing Systems (NIPS), pp. 315–323. NIPS Foundation Inc., Lake Tahoe (2013)
Kiwiel, K.C., Rosa, C.H., Ruszczyński, A.: Proximal decomposition via alternating linearization. SIAM J. Optim. 9(3), 668–689 (1999)
Lan, G., Monteiro, R.D.C.: Iteration complexity of first-order penalty methods for convex programming. Math. Program. 138(1), 115–139 (2013)
Necoara, I., Nesterov, Yu., Glineur, F.: Linear convergence of first order methods for non-strongly convex optimization. Math. Program. (2018). https://doi.org/10.1007/s10107-018-1232-1
Necoara, I., Patrascu, A., Glineur, F.: Complexity of first-order inexact Lagrangian and penalty methods for conic convex programming. Optim. Method Softw. (2017). https://doi.org/10.1080/10556788.2017.1380642
Necoara, I., Suykens, J.A.K.: Interior-point Lagrangian decomposition method for separable convex optimization. J. Optim. Theory Appl. 143(3), 567–588 (2009)
Nemirovskii, A., Yudin, D.: Problem Complexity and Method Efficiency in Optimization. Wiley Interscience, New York (1983)
Nesterov, Y.: A method for unconstrained convex minimization problem with the rate of convergence \({\cal{O}} (1/k^2)\). Doklady AN SSSR 269, 543–547 (1983). Translated as Soviet Math. Dokl
Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course, Volume 87 of Applied Optimization. Kluwer Academic Publishers, Dordrecht (2004)
Nesterov, Y.: Efficiency of coordinate descent methods on huge-scale optimization problems. SIAM J. Optim. 22(2), 341–362 (2012)
Nesterov, Y.: Gradient methods for minimizing composite objective function. Math. Program. 140(1), 125–161 (2013)
Nguyen, V.Q., Fercoq, O., Cevher, V.: Smoothing technique for nonsmooth composite minimization with linear operator. ArXiv preprint (arXiv:1706.05837) (2017)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer Series in Operations Research and Financial Engineering, 2nd edn. Springer, Berlin (2006)
O’Donoghue, B., Candes, E.: Adaptive Restart for Accelerated Gradient Schemes. Found. Comput. Math. 15, 715–732 (2015)
Ouyang, Y., Chen, Y., Lan, G., Pasiliao, E .J.R.: An accelerated linearized alternating direction method of multiplier. SIAM J. Imaging Sci. 8(1), 644–681 (2015)
Recht, B., Fazel, M., Parrilo, P.A.: Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 52(3), 471–501 (2010)
Rockafellar, R.T.: Convex Analysis, Volume 28 of Princeton Mathematics Series. Princeton University Press, Princeton (1970)
Shefi, R., Teboulle, M.: On the rate of convergence of the proximal alternating linearized minimization algorithm for convex problems. EURO J. Comput. Optim. 4(1), 27–46 (2016)
Sra, S., Nowozin, S., Wright, S.J.: Optimization for Machine Learning. MIT Press, Cambridge (2012)
Tran-Dinh, Q., Alacaoglu, A., Fercoq, O., Cevher, V.: Self-adaptive double-loop primal–dual algorithm for nonsmooth convex optimization. ArXiv preprint (arXiv:1808.04648), pp. 1–38 (2018)
Tran-Dinh, Q., Cevher, V.: A primal–dual algorithmic framework for constrained convex minimization. ArXiv preprint (arXiv:1406.5403), Technical Report, pp. 1–54 (2014)
Tran-Dinh, Q., Cevher, V.: Constrained convex minimization via model-based excessive gap. In: Proceedings of the Neural Information Processing Systems (NIPS), vol. 27, pp. 721–729, Montreal, Canada, December (2014)
Tran-Dinh, Q., Fercoq, O., Cevher, V.: A smooth primal–dual optimization framework for nonsmooth composite convex minimization. SIAM J. Optim. 28, 1–35 (2018)
Tran-Dinh, Q.: Construction and iteration-complexity of primal sequences in alternating minimization algorithms. ArXiv preprint (arXiv:1511.03305) (2015)
Tran-Dinh, Q.: Adaptive smoothing algorithms for nonsmooth composite convex minimization. Comput. Optim. Appl. 66(3), 425–451 (2016)
Tran-Dinh, Q.: Non-Ergodic alternating proximal augmented Lagrangian algorithms with optimal rates. In: The 32nd Conference on Neural Information Processing Systems (NIPS), pp. 1–9, NIPS Foundation Inc., Montreal, Canada, December (2018)
Tseng, P.: Applications of splitting algorithm to decomposition in convex programming and variational inequalities. SIAM J. Control Optim. 29, 119–138 (1991)
Tseng, P.: On accelerated proximal gradient methods for convex-concave optimization. Submitted to SIAM J. Optim. (2008)
Vu, C.B.: A splitting algorithm for dual monotone inclusions involving co-coercive operators. Adv. Comput. Math. 38(3), 667–681 (2013)
Woodworth, B.E., Srebro, N.: Tight complexity bounds for optimizing composite objectives. In: Lee, D.D., Sugiyama, M., Luxburg, U.V., Guyon, I., Garnett, R. (eds.), Advances in Neural Information Processing Systems (NIPS), pp. 3639–3647. NIPS Foundation Inc., Barcelona, Spain (2016)
Xu, Y.: Accelerated first-order primal–dual proximal methods for linearly constrained composite convex programming. SIAM J. Optim. 27(3), 1459–1484 (2017)
Zou, H., Hastie, T.: Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 67(2), 301–320 (2005)
Acknowledgements
This work is partly supported by the NSF-grant, DMS-1619884, USA, and the Nafosted grant 101.01-2017.315 (Vietnam).
Author information
Authors and Affiliations
Corresponding author
A Appendix: The proof of technical results in the main text
A Appendix: The proof of technical results in the main text
This appendix provides the full proof of the technical results in the main text.
1.1 A.1 Properties of the distance function \(\mathrm {dist}_{\mathcal {K}}(\cdot )\)
We investigate some necessary properties of \(\psi \) defined by (7) to analyze the convergence of Algorithms 1 and 2. We first consider the following distance function:
where \(r^{*}(u) := \mathrm {proj}_{\mathcal {K}}\left( u\right) \) is the projection of \(u\) onto \(\mathcal {K}\). Clearly, (45) becomes
where \(s_{\mathcal {K}}(\lambda ) := \sup _{r\in \mathcal {K}}\langle \lambda , r\rangle \) is the support function of \(\mathcal {K}\).
The function \(\varphi \) is convex and differentiable. Its gradient is given by
where \(\mathcal {K}^{\circ } := \left\{ v\in \mathbb {R}^n \mid \langle u, v\rangle \le 1, ~u\in \mathcal {K}\right\} \) is the polar set of \(\mathcal {K}\), and \(\nu > 0\) solves \(\nu = \langle \mathrm {proj}_{\mathcal {K}^{\circ }}\left( \nu u\right) , \nu u - \mathrm {proj}_{\mathcal {K}^{\circ }}\left( \nu u\right) \rangle \). If \(\mathcal {K}\) is a cone, then \(\nabla {\varphi }(u) = \mathrm {proj}_{\mathcal {K}^{\circ }}\left( u\right) = \mathrm {proj}_{-\mathcal {K}^{*}}\left( u\right) \), where \(\mathcal {K}^{*} := \left\{ v\in \mathbb {R}^n \mid \langle u, v\rangle \ge 0, ~u\in \mathcal {K}\right\} \) is the dual cone of \(\mathcal {K}\) [3].
By using the property of \(\mathrm {proj}_{\mathcal {K}}(\cdot )\), it is easy to prove that \(\nabla {\varphi }(\cdot )\) is Lipschitz continuous with the Lipschitz constant \(L_{\varphi } = 1\). Hence, for any \(u, v\in \mathbb {R}^n\), we have (see [35]):
Let us recall \(\psi \) defined by (7) as
Then, \(\psi \) is also convex and differentiable, and its gradient is given by
For given \(x^{k+1}\in \mathbb {R}^{p_1}\) and \(\hat{y}^k\in \mathbb {R}^{p_2}\), let us define the following two functions:
Then, the following lemma provides some properties of \(\ell _k\) and \(\mathcal {Q}_k\).
Lemma 4
Let \(z^{\star } = (x^{\star }, y^{\star }) \in \mathbb {R}^{p}\) be such that \(Ax^{\star } + By^{\star } - c\in \mathcal {K}\). Then, for \(\ell _k\) defined by (51) and \(\psi \) defined by (49), we have
where \(\hat{s}^{k+1} := Ax^{k+1} + B\hat{y}^k - c- \mathrm {proj}_{\mathcal {K}}\big (Ax^{k+1} + B\hat{y}^k - c\big )\) and \(s^k := Ax^k + By^k - c- \mathrm {proj}_{\mathcal {K}}\big (Ax^k + By^k - c\big )\). Moreover, we also have
Proof
Since \(Ax^{\star } + By^{\star } - c\in \mathcal {K}\), if we define \(r^{\star } := Ax^{\star } + By^{\star } - c\), then \(r^{\star } \in \mathcal {K}\). Let \(\hat{u}^{k} := Ax^{k+1} + B\hat{y}^k - c\in \mathbb {R}^n\). We can derive
which is the first inequality of (52). Here, we use the property \(\langle \hat{u}^{k} - \mathrm {proj}_{\mathcal {K}}(\hat{u}^{k}), r^{\star } - \mathrm {proj}_{\mathcal {K}}(\hat{u}^{k})\rangle \le 0\) for any \(r^{\star }\in \mathcal {K}\) of the projection \(\mathrm {proj}_{\mathcal {K}}\). The second inequality of (52) follows directly from (48) and the definition of \(\psi \) in (49). The proof of (53) can be found in [35] due to the Lipschitz continuity of \(\nabla _y\psi (x^{k+1},\cdot )\). \(\square \)
1.2 A.2 Descent property of the alternating scheme in Algorithms 1 and 2
Lemma 5
Let \(\ell _k\) and \(\mathcal {Q}_k\) be defined by (51), and \(\varPhi _{\rho }\) be defined by (7).
-
(a)
Let \(z^{k+1} := (x^{k+1}, y^{k+1})\) be generated by Step 3 of Algorithm 1. Then, for any \(z:= (x, y) \in \mathrm {dom}(F)\), we have
$$\begin{aligned} \varPhi _{\rho _k}(z^{k+1})\le & {} F(z) + \rho _k\ell _k(z) + \gamma _k\langle x^{k+1} - \hat{x}^k, x- \hat{x}^k\rangle - \gamma _k\Vert x^{k+1} - \hat{x}^k\Vert ^2 \nonumber \\&+ \rho _k\Vert B\Vert ^2\langle y^{k + 1} - \hat{y}^k, y-\hat{y}^k\rangle - \frac{\rho _k\left\| B\right\| ^2}{2}\Vert y^{k+ 1} - \hat{y}^k\Vert ^2. \end{aligned}$$(54) -
(b)
Alternatively, let \(z^{k+1} := (x^{k+1}, y^{k+1})\) be generated by Step 4 of Algorithm 2, and \(\breve{y}^{k+1} := (1-\tau _k)y^k + \tau _k\tilde{y}^{k+1}\). Then, for any \(z:= (x, y) \in \mathrm {dom}(F)\), we have
$$\begin{aligned} \breve{\varPhi }_{k+1}:= & {} f(x^{k+1}) + g(\breve{y}^{k+1}) + \rho _k\mathcal {Q}_k(\breve{y}^{k+1}) \nonumber \\\le & {} (1-\tau _k) \big [ F(z^{k}) + \rho _k\ell _k(z^k) \big ] + \tau _k\big [ F(z) + \rho _k\ell _k(z) \big ] \nonumber \\&+ \tfrac{\gamma _0\tau _k^2}{2}\Vert \tilde{x}^k - x\Vert ^2 - \tfrac{\gamma _0\tau _k^2}{2}\Vert \tilde{x}^{k+1} - x\Vert ^2 \nonumber \\&+ \tfrac{\rho _k\tau _k^2\Vert B\Vert ^2}{2}\Vert \tilde{y}^k - y\Vert ^2 - \tfrac{\left( \rho _k\tau _k^2\Vert B\Vert ^2 + \mu _g\tau _k\right) }{2}\Vert \tilde{y}^{k+1} - y\Vert ^2. \end{aligned}$$(55)
Proof
(a) Combining the optimality condition of two subproblems at Step 3 of Algorithm 1, and the convexity of f and g, we can derive
Using (53) with \(y= y^{k+1}\), we have
Combining the last estimate and (56), and then using (7), we can derive
which is exactly (54).
(b) First, from the definition of \(\ell _k\) and \(\mathcal {Q}_k\) in (51), using \(\breve{y}^{k+1} - \hat{y}^k = \tau _k(\tilde{y}^{k+1} - \tilde{y}^k)\) and \(x^{k+1} - (1-\tau _k)x^k - \tau _k\tilde{x}^{k+1} = 0\), we can show that
By the convexity of f, \(\tau _k\tilde{x}^{k+1} = x^{k+1} - (1-\tau _k)x^k\) from (18), and the optimality condition of the x-subproblem at Step 4 of Algorithm 2, we can derive
for any \(x\in \mathbb {R}^{p_1}\), where \(\nabla {f}(x^{k + 1})\in \partial {f}(x^{k + 1})\).
By the \(\mu _g\)-strong convexity of g, \(\breve{y}^{k+1} := (1-\tau _k)y^k + \tau _k\tilde{y}^{k+1}\), and the optimality condition of the y-subproblem at Step 4 of Algorithm 2, one can also derive
for any \(y\in \mathbb {R}^{p_2}\), where \(\nabla {g}(\tilde{y}^{k+1}) \in \partial {g}(\tilde{y}^{k+1})\).
Combining this, (57), (58) and (59) and then using \(\breve{\varPhi }_k\), we have
Next, using (18), for any \(z= (x, y)\in \mathrm {dom}(F)\), we also have
Substituting (61) into (60) we obtain
which is exactly (55) by neglecting the term \(-\frac{\gamma _0}{2}\Vert x^{k+1} - \hat{x}^k\Vert ^2\). \(\square \)
1.3 A.3 The proof of Lemma 2: the key estimate of Algorithm 1
Using the fact that \(\tau _k = \frac{1}{k+1}\), we have \(\frac{\tau _{k+1}(1-\tau _k)}{\tau _k} = \frac{k}{k+2}\). Hence, the third line of Step 3 of Algorithm 1 can be written as
This step can be split into two steps with \((\hat{x}^k, \hat{y}^k)\) and \((\tilde{x}^k, \tilde{y}^k)\) as in (14), which is standard in accelerated gradient methods [4, 35]. We omit the detailed derivation.
Next, we prove (15). Using (52), we have
Using (54) with \((x, y) = (x^k, y^k)\) and \((x, y) = (x^{\star }, y^{\star })\) respectively, we obtain
Multiplying the first inequality by \(1 - \tau _k \in [0, 1]\) and the second one by \(\tau _k \in [0, 1]\), and summing up the results, then using \(\hat{x}^k - (1-\tau _k)x^k = \tau _k\tilde{x}^k\) and \(\hat{y}^k - (1-\tau _k)y^k = \tau _k\tilde{y}^k\) from (14), we obtain
By the update rule in (14) we can show that
Using this relation and \(\varPhi _{\rho _{k}}(z^k) = \varPhi _{\rho _{k-1}}(z^k) + \frac{(\rho _k - \rho _{k-1})}{2}\Vert s^k\Vert ^2\) into (63), we get
where \(R_k\) is defined as
Using (65) into (64) and ignoring \(-\frac{\gamma _k}{2}\Vert x^{k+1} - \hat{x}^k\Vert ^2\), we obtain (15). \(\square \)
1.4 A.4 The proof of Lemma 3: the key estimate of Algorithm 2
The proof of (18) is similar to the proof of (14), and we skip its details here.
Using \(z= z^{\star }\) and (52) into (55), we obtain
From the definition of \(\psi \) in (49) and (52), we have
Using these expressions into (66), we obtain
where \(R_k\) is defined as (65).
Let us consider two cases:
-
For Option 1 at Step 5 of Algorithm 2, we have \(y^{k+1} = \breve{y}^{k+1}\). Hence, using (53), we get
$$\begin{aligned} \varPhi _{\rho _k}(z^{k+1}) = f(x^{k+1}) + g(y^{k+1}) + \rho _k\psi (x^{k+1},y^{k+1}) \le \breve{\varPhi }_{k+1}. \end{aligned}$$(68) -
For Option 2 at Step 5 of Algorithm 2, we have
$$\begin{aligned} \varPhi _{\rho _k}(z^{k+1})\le & {} f(x^{k+1}) + g(y^{k+1}) + \rho _k\mathcal {Q}_k(y^{k+1}) \nonumber \\= & {} f(x^{k+1}) + \displaystyle \min _{y\in \mathbb {R}^{p_2}}\Big \{ g(y) + \rho _k\mathcal {Q}_k(y) \Big \} \nonumber \\\le & {} f(x^{k+1}) + g(\breve{y}^{k+1}) + \rho _k\mathcal {Q}_k(\breve{y}^{k+1}) = \breve{\varPhi }_{k+1}. \end{aligned}$$(69)
Using either (68) or (69) into (67), we obtain
Using the lower bound (65) of \(R_k\) into this inequality, we obtain (19). \(\square \)
1.5 A.5 The proof of Corollary 1: application to composite convex minimization
By the \(L_f\)-Lipschitz continuity of f and Lemma 1, we have
where \(S_{\rho }(z) := \varPhi _{\rho }(z) - P^{\star }\). This inequality also leads to
Since using (23) is equivalent to applying Algorithm 1 to its constrained reformulation, by (16), we have
Using these expressions into (71) we get
Substituting this into (70) and using the bound of \(S_{\rho _{k-1}}\), we obtain (25).
Now, if we use (24), then it is equivalent to applying Algorithm 2 with Option 1 to solve its constrained reformulation. In this case, from the proof of Theorem 2, we can derive
Combining these estimates and (71), we have \(\Vert x^k - y^k\Vert \le \tfrac{8(L_f + (\rho _0 + \mu _g)\Vert y^0 - y^{\star }\Vert )}{\rho _0(k+1)^2}\). Substituting this into (70) and using the bound of \(S_{\rho _{k-1}}\) we obtain (26). \(\square \)
1.6 A.6 The proof of Theorem 3: extension to the sum of three objective functions
Using the Lipschitz gradient continuity of h and [35, Theorem 2.1.5], we have
In addition, the optimality condition of (34) is
Using these expressions and the same argument as the proof of Lemma 5, we derive
Finally, with the same proof as in (15), and \(\hat{\beta }_k = \Vert B\Vert ^2\rho _k + L_h\), we can show that
where \(s^k := Ax^k + By^k - c- \mathrm {proj}_{\mathcal {K}}\big (Ax^k + By^k - c\big )\). In order to telescope, we impose conditions on \(\rho _k\) and \(\tau _k\) as
If we choose \(\tau _{k} = \frac{1}{k+1}\), then \(\rho _k = \rho _0(k+1)\). The first condition above becomes
which certainly holds.
The remaining proof of the first part in Corollary 3 is similar to the proof of Theorem 1, but with \(R_p^2 := \gamma _0 \Vert x^0 - x^{\star }\Vert ^2 + (L_h + \rho _0\Vert B\Vert ^2)\Vert y^0 - y^{\star }\Vert ^2\) due to (73).
We now prove the second part of Corollary 3. For the case (i) with \(\mu _g > 0\), the proof is very similar to the proof of Theorem 2, but \(\rho _k\Vert B\Vert ^2\) is changed to \(\hat{\beta }_k\) and is updated as \(\hat{\beta }_k = \rho _k\left\| B\right\| ^2 + L_h\). We omit the detail of this analysis here. We only prove the second case (ii) when \(L_h < 2\mu _h\).
Using the convexity and the Lipschitz gradient continuity of h, we can derive
Using this estimate, with a similar proof as of (60), we can derive
Here, we use the optimality condition of (10) and (35) into the last inequality, and \(\nabla f, \nabla g\), and \(\nabla h\) are subgradients of f, g, and h, respectively.
Using the same argument as the proof of (19), if we denote \(S_k := \varPhi _{\rho _{k-1}}(z^k) - F^{\star }\), then the last inequality above together with (36) leads to
where \(s^k := Ax^k + By^k - c- \mathrm {proj}_{\mathcal {K}}\big (Ax^k + By^k - c\big )\). We still choose the update rule for \(\tau _k\), \(\rho _k\) and \(\gamma _k\) as in Algorithm 2. Then, in order to telescope this inequality, we impose the following conditions:
Using the first condition into the second one and noting that \(1 - \tau _k = \frac{\tau _k^2}{\tau _{k-1}^2}\) and \(\rho _k = \frac{\rho _0}{\tau _k^2}\), we obtain \( \rho _0\left\| B\right\| ^2 + L_h - \mu _h \le \frac{\tau _k}{\tau _{k-1}}(L_h + \mu _g)\). This condition holds if \(\rho _0 \le \frac{\mu _g + 2\mu _h - L_h}{2\Vert B\Vert ^2} > 0\). Using (74) we have the same conclusion as in Theorem 2. \(\square \)
Rights and permissions
About this article
Cite this article
Tran-Dinh, Q. Proximal alternating penalty algorithms for nonsmooth constrained convex optimization. Comput Optim Appl 72, 1–43 (2019). https://doi.org/10.1007/s10589-018-0033-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-018-0033-z
Keywords
- Proximal alternating algorithm
- Quadratic penalty method
- Accelerated scheme
- Constrained convex optimization
- First-order methods
- Convergence rate