A generative model and a generalized trust region Newton method for noise reduction

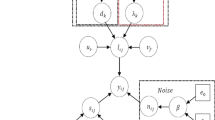
Abstract

In practical applications related to, for instance, machine learning, data mining and pattern recognition, one is commonly dealing with noisy data lying near some low-dimensional manifold. A well-established tool for extracting the intrinsically low-dimensional structure from such data is principal component analysis (PCA). Due to the inherent limitations of this linear method, its extensions to extraction of nonlinear structures have attracted increasing research interest in recent years. Assuming a generative model for noisy data, we develop a probabilistic approach for separating the data-generating nonlinear functions from noise. We demonstrate that ridges of the marginal density induced by the model are viable estimators for the generating functions. For projecting a given point onto a ridge of its estimated marginal density, we develop a generalized trust region Newton method and prove its convergence to a ridge point. Accuracy of the model and computational efficiency of the projection method are assessed via numerical experiments where we utilize Gaussian kernels for nonparametric estimation of the underlying densities of the test datasets.

Appendix: Proofs of Theorem 2.1 and Lemmata 3.1 and 3.6

Theorem 2.1

Let m>0, $\mathcal{D}=\{\boldsymbol{\theta}\in\mathbb{R}^{d}\mid a_{i}\leq \theta_{i}\leq b_{i},i=1,2,\dots,m\}$ with a _i <b _i , i=1,2,…,m and let $\boldsymbol{f}:\mathcal{D}\to\mathbb{R}^{d}$ be defined as

$$ \boldsymbol{f}(\boldsymbol{\theta})=\boldsymbol{x}_0+\sum _{i=1}^m\theta_i \boldsymbol{v}_i $$

with some $\boldsymbol{x}_{0}\in\mathbb{R}^{d}$ and mutually orthogonal vectors $\{\boldsymbol{v}_{i}\}_{i=1}^{m}\subset\mathbb{R}^{d}\setminus\{\boldsymbol{0}\}$. If p is defined by Eq. (5) with n=1 and f ₁=f, then $\{\boldsymbol{f}(\boldsymbol{\theta}) \mid\boldsymbol{\theta}\in\mathcal{D}\}\subseteq R_{p}^{m}$.

Proof

Without loss of generality we can assume that x ₀=0 and

$$ \boldsymbol{f}(\boldsymbol{\theta})=\sum _{i=1}^m\theta_i \boldsymbol{e}_i, $$

(38)

where $\boldsymbol{e}_{i}\in\mathbb{R}^{d}$ denotes a unit vector along the i-th coordinate axis. With some noise standard deviation σ>0, the gradient and Hessian of the marginal density (5) induced by the model of Sect. 2.1 with this function are

$$ \nabla p(\boldsymbol{x})= -\frac{C_{\sigma}}{V(\mathcal{D})} \int _{\mathcal{D}}\boldsymbol{r} (\boldsymbol{x};\boldsymbol{\theta}) \exp \left (-\frac {\|\boldsymbol{r}(\boldsymbol {x};\boldsymbol{\theta})\|^2}{2\sigma ^2}\right )d\boldsymbol{ \theta} $$

(39)

and

$$ \begin{aligned}[b] \nabla^2 p( \boldsymbol{x}) = & \frac{C_{\sigma}}{V(\mathcal{D})}\int _{\mathcal{D}} \biggl[\frac{ \boldsymbol{r}(\boldsymbol{x};\boldsymbol{\theta})\boldsymbol{r}(\boldsymbol {x};\boldsymbol{\theta})}{\sigma^2}- \boldsymbol{I} \biggr] \exp \left (-\frac {\|\boldsymbol{r}(\boldsymbol{x};\boldsymbol{ \theta}\|^2}{2\sigma ^2}\right )d \boldsymbol{\theta} \\ = & \frac{C_{\sigma}}{V(\mathcal{D})\sigma^2}\int _{\mathcal{D}} \boldsymbol{r}(\boldsymbol{x};\boldsymbol{ \theta})\boldsymbol{r}(\boldsymbol {x};\boldsymbol{\theta})^T \exp \left (-\frac {\|\boldsymbol{r}(\boldsymbol{x}; \boldsymbol{\theta})\|^2}{2\sigma ^2}\right )d\boldsymbol{ \theta}-\frac{p(\boldsymbol{x})}{ \sigma^2}\boldsymbol{I}, \end{aligned} $$

(40)

where

$$ \boldsymbol{r}(\boldsymbol{x};\boldsymbol{\theta})=\boldsymbol{x}-\sum _{i=1 }^m\theta_i\boldsymbol{e}_i \quad\mbox{and}\quad C_{\sigma}=\frac{1}{(2\pi)^{\frac{d}{2}}\sigma^{d+2}}, $$

respectively, and I denotes the d×d identity matrix.

By Proposition 2.2, it suffices to consider the logarithm of the density p. For the Hessian of the logarithm of p, we obtain the expression

$$ \nabla^2\log{p}(\boldsymbol{x})= \frac{\nabla^2 p(\boldsymbol{x})}{p(\boldsymbol{x})}-\frac{\nabla p( \boldsymbol{x})\nabla p(\boldsymbol{x})^T}{p(\boldsymbol{x})^2}. $$

(41)

Since $\sum_{j=1}^{m}\theta_{j}\boldsymbol{e}_{j}^{T}\boldsymbol{e}_{i}=0$ for all i=m+1,m+2,…,d, from Eqs. (39) and (40) we obtain

$$ \begin{aligned}[b] \nabla p(\boldsymbol{x})^T \boldsymbol{e}_i & = -\frac{C_{\sigma}}{V(\mathcal{D})}\int _{\mathcal{D}} \Biggl(\boldsymbol {x}-\sum_{j=1}^m\theta_j \boldsymbol{e}_j \Biggr)^T\boldsymbol{e}_i \exp \left (-\frac { \|\boldsymbol{r}(\boldsymbol{x};\boldsymbol{\theta})\|^2}{2\sigma ^2}\right )d\boldsymbol{ \theta} \\ & = -\boldsymbol{x}^T\boldsymbol{e}_i\frac{C_{\sigma}}{V(\mathcal{D})} \int _{\mathcal{D}}\exp \left (-\frac {\|\boldsymbol{r}(\boldsymbol{x};\boldsymbol { \theta})\|^2}{2\sigma ^2}\right )d\boldsymbol{\theta}= -\frac{x_i p(\boldsymbol{x})}{\sigma^2} \end{aligned} $$

(42)

and

$$\begin{aligned} \nabla^2 p(\boldsymbol{x})\boldsymbol{e}_i & = \frac{C_{\sigma}}{V(\mathcal{D})\sigma^2}\int _{\mathcal{D}} \Biggl( \boldsymbol{x}-\sum _{j=1}^m\theta_j\boldsymbol{e}_j \Biggr) \Biggl(\boldsymbol {x}-\sum_{j=1}^m \theta_j\boldsymbol{e}_j \Biggr)^T \boldsymbol{e}_i \\ &\quad {}\times \exp \left (-\frac { \|\boldsymbol{r}(\boldsymbol{x}; \boldsymbol{\theta})\|^2}{2\sigma ^2}\right )d\boldsymbol{\theta} -\frac{p(\boldsymbol{x})}{\sigma^2} \boldsymbol{e}_i \\ & = \boldsymbol{x}^T\boldsymbol{e}_i\frac{C_{\sigma}}{V(\mathcal{D})\sigma^2} \int _{\mathcal{D}}\boldsymbol{r}(\boldsymbol{x};\boldsymbol{\sigma}) \exp \left (-\frac {\|\boldsymbol{r}(\boldsymbol{x};\boldsymbol{\theta})\|^2}{2\sigma ^2}\right )d \boldsymbol{ \theta}-\frac{p(\boldsymbol{x})}{\sigma^2}\boldsymbol{e}_i \\ & = -\frac{x_i}{\sigma^2}\nabla p(\boldsymbol{x})-\frac{p(\boldsymbol{x})}{ \sigma^2} \boldsymbol{e}_i \end{aligned}$$

for all i=m+1,m+2,…,d. Substituting these expressions into Eq. (41) yields

$$ \nabla^2\log p(\boldsymbol{x})\boldsymbol{e}_i= - \frac{\boldsymbol{e}_i}{\sigma^2} $$

for all i=m+1,m+2,…,d, which shows that the vectors e _m+1,e _m+2,…,e _d span the d−m-dimensional eigenspace of the matrix ∇²logp(x) corresponding to the eigenvalue $-\frac{1}{\sigma^{2}}$ for all $\boldsymbol{x}\in\mathbb{R}^{d}$. Consequently, condition (6b) for logp(x) holds for all $\boldsymbol{x}\in\mathbb{R}^{d}$. Furthermore, by Eq. (42) and the fact that p(x)>0 for all $\boldsymbol{x}\in\mathbb{R}^{d}$, condition (6a) for logp(x) holds if and only if x∈ span(e ₁,e ₂,…,e _m ).

On the other hand, from Eqs. (39)–(41) we obtain

$$\begin{aligned} \boldsymbol{e}_i^T\nabla^2\log{p}( \boldsymbol{x})\boldsymbol{e}_i & = \frac{\boldsymbol{e}_i^T\nabla^2 p(\boldsymbol{x})\boldsymbol{e}_i}{p( \boldsymbol{x})}- \frac{\boldsymbol{e}_i^T\nabla p(\boldsymbol{x})\nabla p( \boldsymbol{x})^T\boldsymbol{e}_i}{p(\boldsymbol{x})^2} \\ & = -\frac{1}{\sigma^2}+F_{\sigma,i}(\boldsymbol{x}) \end{aligned}$$

for all i=1,2,…,m, where

$$\begin{aligned} F_{\sigma,i}(\boldsymbol{x}) &= \frac{C_{\sigma}}{p(\boldsymbol{x})V(\mathcal{D})\sigma^2}\int _{ \mathcal{D}}(x_i- \theta_i)^2\exp \left (-\frac {\|\boldsymbol{r}(\boldsymbol{x}; \boldsymbol{\theta})\|^2}{2\sigma ^2}\right )d\boldsymbol{\theta} \\ & \quad {}-\frac{C_{\sigma}}{p(\boldsymbol{x})^2 V(\mathcal{D})} \biggl[\int _{ \mathcal{D}}(x_i-\theta_i) \exp \left (-\frac {\|\boldsymbol{r}(\boldsymbol{x}; \boldsymbol{\theta})\|^2}{2\sigma ^2}\right )d\boldsymbol{ \theta} \biggr]^2. \end{aligned}$$

Since it can be shown that F _σ,i (x)>0 for all $\boldsymbol{x}\in\mathbb{R}^{d}$ and i=1,2,…,m, we observe that

$$ \boldsymbol{e}_i^T\nabla^2\log{p}( \boldsymbol{x})\boldsymbol{e}_i= -\frac{1}{\sigma^2}+F_{\sigma,i}( \boldsymbol{x})>-\frac{1}{\sigma^2}= \boldsymbol{e}_j^T \nabla^2\log{p}(\boldsymbol{x})\boldsymbol{e}_j $$

for all i=1,2,…,m and j=m+1,m+2,…,d. This shows that the eigenvalues of ∇²logp(x) corresponding to the eigenvectors in the subspace spanned by the vectors e ₁,e ₂,…,e _m are strictly greater than the remaining ones for all $\boldsymbol{x}\in\mathbb{R}^{d}$. Thus, the eigenvalues of ∇²logp(x) satisfy condition (6c) for all $\boldsymbol{x}\in\mathbb{R}^{d}$. Since we showed above that for logp(x), condition (6b) holds for all $\boldsymbol{x}\in\mathbb{R}^{d}$ and condition (6a) holds if and only if $\boldsymbol{x}\in\operatorname{span}(\boldsymbol{e}_{1},\boldsymbol{e}_{2}, \dots,\boldsymbol{e}_{m})$, this implies that $R_{\log{p}}^{m}=\operatorname{span}( \boldsymbol{e}_{1},\boldsymbol{e}_{2},\dots,\boldsymbol{e}_{m})$. By Eq. (38) and Proposition 2.2, we then obtain that $\{f(\boldsymbol{\theta})\mid\boldsymbol{\theta}\in \mathcal{D}\}\subseteq R_{\log{p}}^{m}=R_{p}^{m}$. □

For the proof of Lemma 3.1 we need the following result.

Lemma A.1

Let $\boldsymbol{H}\in\mathbb{R}^{d\times d}$ be a symmetric matrix and define

$$ \boldsymbol{V}=[\boldsymbol{v}_{m+1},\boldsymbol{v}_{m+2}, \dots,\boldsymbol {v}_d]\in\mathbb{R}^{d\times(d-m)} $$

and

$$ \boldsymbol{\varLambda}=\operatorname{diag}[\lambda_{m+1}, \lambda_{m+2},\dots, \lambda_d]\in\mathbb{R}^{(d-m)\times(d-m)}, $$

where $\{\boldsymbol{v}_{i}\}_{i=m+1}^{d}$ denote the orthonormal eigenvectors of H corresponding to its eigenvalues λ _m+1≥λ _m+2≥…≥λ _d . If we define $\tilde{\boldsymbol{H}}=\boldsymbol {V}^{T}\boldsymbol{H}\boldsymbol{V}$, then $\tilde{\boldsymbol{H}}=\boldsymbol{ \varLambda}$. Furthermore, if we let $\boldsymbol{s}\in\operatorname{span}(\boldsymbol {v}_{m+1},\boldsymbol{v}_{m+2},\dots,\boldsymbol{v}_{d})$ and $\boldsymbol{g}\in \mathbb{R}^{d}$ and define $\tilde{\boldsymbol{s}}=\boldsymbol{V}^{T}\boldsymbol{s }$ and

$$ Q(\boldsymbol{s})=\boldsymbol{g}^T\boldsymbol{s}+\frac{1}{2} \boldsymbol{s}^T \boldsymbol{H}\boldsymbol{s} \quad\mbox{\textit{and}}\quad \tilde{Q}(\tilde{\boldsymbol{s}})=\tilde{\boldsymbol{g}}^T\tilde{ \boldsymbol {s}}+\frac{1}{2}\tilde{\boldsymbol{s}}^T\tilde{ \boldsymbol{H}}\tilde{ \boldsymbol{s}} $$

with $\tilde{\boldsymbol{g}}=\boldsymbol{V}^{T}\boldsymbol{g}$, then we have $Q( \boldsymbol{s})=\tilde{Q}(\tilde{\boldsymbol{s}})$, $\|\boldsymbol{s}\|=\| \tilde{\boldsymbol{s}}\|$ and $\boldsymbol{s}=\boldsymbol{V}\tilde{\boldsymbol {s}}$.

Proof

In order to show that $\tilde{\boldsymbol{H}}=\boldsymbol{\varLambda}$, we define the matrices

$$ \boldsymbol{W}=[\boldsymbol{v}_1,\boldsymbol{v}_2,\dots, \boldsymbol{v}_d] \in\mathbb{R}^{d\times d} \quad\mbox{and}\quad \boldsymbol{U}=\operatorname{diag}[\lambda_1,\lambda_2,\dots, \lambda_d]\in \mathbb{R}^{d\times d}, $$

where $\{\boldsymbol{v}_{i}\}_{i=1}^{d}$ denote the eigenvectors of H corresponding to its eigenvalues λ ₁≥λ ₂≥…≥λ _d . By the definition $\tilde{\boldsymbol{H}}=\boldsymbol{V}^{T} \boldsymbol{H}\boldsymbol{V}$ and the eigendecomposition H=WUW ^T, we have

$$ \tilde{\boldsymbol{H}}= \boldsymbol{V}^T\boldsymbol{H} \boldsymbol{V}= \boldsymbol{V}^T\boldsymbol{W}\boldsymbol{U} \boldsymbol{W}^T\boldsymbol{V}= \boldsymbol{V}^T \Biggl[ \sum_{i=1}^d\lambda_i \boldsymbol{v}_i\boldsymbol{v }_i^T \Biggr] \boldsymbol{V}= \sum_{i=m+1}^d \boldsymbol{e}_{i-m}\boldsymbol{e}_{i-m}^T \lambda_i= \boldsymbol{\varLambda}, $$

where e _i denotes a d−m-dimensional unit vector along the i-th coordinate axis.

Since the vectors $\{\boldsymbol{v}_{i}\}_{i=m+1}^{d}$ span an orthonormal basis, we have s=VV ^T s for all $\boldsymbol{s}\in\operatorname{span}(\boldsymbol{v}_{m+1},\boldsymbol{v}_{m+2},\dots, \boldsymbol{v}_{d})$. Thus, by the definition $\tilde{\boldsymbol{s}}= \boldsymbol{V}^{T}\boldsymbol{s}$, for any such s we obtain

$$ Q(\boldsymbol{s})= \boldsymbol{g}^T\boldsymbol{s}+\frac{1}{2} \boldsymbol{s}^T\boldsymbol{H} \boldsymbol{s}= \boldsymbol{g}^T \boldsymbol{V}\boldsymbol{V}^T\boldsymbol{s}+\frac{1}{2} \boldsymbol{s}^T\boldsymbol{V}\boldsymbol{V}^T \boldsymbol{H}\boldsymbol {V}\boldsymbol{V}^T\boldsymbol{s}= \tilde{ \boldsymbol{g}}^T\tilde{\boldsymbol{s}}+\frac{1}{2}\tilde{ \boldsymbol{s}}^T\tilde{\boldsymbol{H}}\tilde{\boldsymbol{s}}= \tilde{Q}(\tilde{\boldsymbol{s}}) $$

and also $\boldsymbol{s}=\boldsymbol{V}\boldsymbol{V}^{T}\boldsymbol{s}= \boldsymbol{V}\tilde{\boldsymbol{s}}$.

Finally, for $\boldsymbol{s}\in\operatorname{span}(\boldsymbol{v}_{m+1},\boldsymbol{v }_{m+2},\dots,\boldsymbol{v}_{d})$ and $\tilde{\boldsymbol{s}}=\boldsymbol{V}^{T} \boldsymbol{s}$, by expressing s as a linear combination of the orthonormal basis vectors $\{\boldsymbol{v}_{i}\}_{i=1}^{d}$ that span $\mathbb{R }^{d}$, we obtain

$$ \|\boldsymbol{s}\|^2= \Biggl\|\sum_{i=1}^d \boldsymbol{v}_i^T\boldsymbol{s}\boldsymbol{v}_i \Biggr\|^2= \Biggl\|\sum_{i=m+1}^d \boldsymbol{v}_i^T\boldsymbol{s}\boldsymbol{v}_i \Biggr\|^2= \sum_{i=m+1}^d\bigl( \boldsymbol{v}_i^T\boldsymbol{s}\bigr)^2= \bigl\| \boldsymbol{V}^T\boldsymbol{s}\bigr\|^2= \|\tilde{ \boldsymbol{s}}\|^2. $$

 □

Lemma 3.1

Let $\boldsymbol{g}\in\mathbb{R}^{d}$ and let $\boldsymbol{H}\in\mathbb{R}^{d \times d}$ be a symmetric matrix and define

$$ Q(\boldsymbol{s})=\boldsymbol{g}^T\boldsymbol{s}+\frac{1}{2} \boldsymbol{s}^T \boldsymbol{H}\boldsymbol{s}. $$

Let 0≤m<d, Δ>0 and let λ _m+1≥λ _m+2≥…≥λ _d and $\{\boldsymbol{v}_{i}\}_{i=m+1}^{d}$ denote the d−m smallest eigenvalues and the corresponding normalized eigenvectors of H, respectively. A vector $\boldsymbol{s}^{*}\in\mathbb{R}^{d}$ is a solution to the problem

$$ \max_{\boldsymbol{s}} \quad Q( \boldsymbol{s}) \quad\mbox{\textit{s.t.}} \quad \|\boldsymbol{s}\| \leq\varDelta \mbox{ \textit{and} } \boldsymbol{s}\in\operatorname{span}(\boldsymbol{v}_{ m+1}, \boldsymbol{v}_{m+2}\dots,\boldsymbol{v}_d) $$

(43)

if s ^∗ is feasible and the conditions

$$\begin{aligned} & \boldsymbol{V}(\boldsymbol{ \varLambda}-\kappa\boldsymbol{I})\boldsymbol{V}^T \boldsymbol{s}^*=- \boldsymbol{V}\boldsymbol{V}^T\boldsymbol{g}, \end{aligned}$$

(44)

$$\begin{aligned} & \kappa\bigl(\varDelta-\| \boldsymbol{s}^*\|\bigr)=0, \end{aligned}$$

(45)

$$\begin{aligned} & \boldsymbol{V}(\boldsymbol{ \varLambda}-\kappa\boldsymbol{I})\boldsymbol{V}^T \quad\mbox{is negative semidefinite} \end{aligned}$$

(46)

hold for some κ≥0, where

$$\begin{aligned} \boldsymbol{V} &= [\boldsymbol{v}_{m+1},\boldsymbol{v}_{m+2}, \dots,\boldsymbol{v}_d]\in\mathbb{R}^{d\times(d-m)}, \\ \boldsymbol{\varLambda} &= \operatorname{diag}[\lambda_{m+1}, \lambda_{m+2},\dots, \lambda_d]\in\mathbb{R}^{(d-m)\times(d-m)} \end{aligned}$$

and I is the (d−m)×(d−m) identity matrix.

Proof

Define $\tilde{\boldsymbol{g}}=\boldsymbol{V}^{T}\boldsymbol{g}$ and $\tilde{ \boldsymbol{H}}=\boldsymbol{V}^{T}\boldsymbol{H}\boldsymbol{V}$. By Theorem 4.1 of [27], a vector $\tilde{\boldsymbol{s}}^{*}\in\mathbb{R}^{d-m}$ is a solution to the problem

$$ \max_{\tilde{\boldsymbol{s}}} \quad \tilde{Q}(\tilde{\boldsymbol{s}}) \quad \mbox{s.t.} \quad \|\tilde{\boldsymbol{s}}\|\leq \varDelta, $$

(47)

where

$$ \tilde{Q}(\tilde{\boldsymbol{s}})= \tilde{\boldsymbol{g}}^T\tilde{ \boldsymbol{s}}+\frac{1}{2}\tilde{\boldsymbol {s}}^T\tilde{ \boldsymbol{H}}\tilde{\boldsymbol{s}} $$

if

$$\begin{aligned} & (\tilde{\boldsymbol{H}}-\kappa \boldsymbol{I}) \tilde{\boldsymbol{s}}^*=-\tilde{\boldsymbol{g}}, \end{aligned}$$

(48)

$$\begin{aligned} & \kappa\bigl(\varDelta-\|\tilde{ \boldsymbol{s}}^*\|\bigr)=0, \end{aligned}$$

(49)

$$\begin{aligned} & \tilde{\boldsymbol{H}}-\kappa \boldsymbol{I} \quad\mbox{is negative semidefinite} \end{aligned}$$

(50)

for some κ≥0.

Assume then that $\boldsymbol{s}^{*}\in\mathbb{R}^{d}$ is in the feasible set of problem (43), that is, $\boldsymbol{s}^{*}\in\operatorname{span}( \boldsymbol{v}_{m+1},\boldsymbol{v}_{m+2},\dots,\boldsymbol{v}_{d})$ and ∥s ^∗∥≤Δ. In addition, assume that conditions (44)–(46) are satisfied with some κ≥0. Let $\tilde{\boldsymbol{s}}^{*}=\boldsymbol{V}^{T} \boldsymbol{s}$. By Lemma A.1 we have $\tilde{ \boldsymbol{H}}=\boldsymbol{\varLambda}$. Thus, by premultiplying condition (44) by V ^T we obtain $(\tilde{ \boldsymbol{H}}-\kappa\boldsymbol{I})\boldsymbol{V}^{T}\boldsymbol{s}^{*}=- \boldsymbol{V}^{T}\boldsymbol{g}$. By the definitions of $\tilde{\boldsymbol{s} }^{*}$ and $\tilde{\boldsymbol{g}}$, this is equivalent to condition (48). In addition, since by Lemma A.1 we have $\|\boldsymbol{s}^{*}\|=\|\tilde{ \boldsymbol{s}}^{*}\|$, condition (45) implies condition (49) and the condition that $\|\tilde {\boldsymbol{s}}\|\leq\varDelta$. Finally, since the matrices V(Λ−κ I)V ^T and Λ−κ I have the same nonzero eigenvalues and $\boldsymbol{\varLambda}=\tilde{\boldsymbol{H}}$ by Lemma A.1, condition (46) implies condition (50). Hence, $\tilde{ \boldsymbol{s}}^{*}$ is a solution to problem (47).

By Lemma A.1 we have $Q(\boldsymbol{s}^{*})=\tilde{Q} (\tilde{\boldsymbol{s}}^{*})$. Assume then that there exists $\boldsymbol{u}\in \mathbb{R}^{d}$ that is in the feasible set of problem (43) such that Q(u)>Q(s ^∗). By Lemma A.1, this implies that $Q(\boldsymbol{u})=\tilde {Q}(\tilde{\boldsymbol{u}})>\tilde{Q}(\tilde{\boldsymbol{s}}^{*})=Q(\boldsymbol {s}^{*})$, where $\tilde{\boldsymbol{u}}=\boldsymbol{V}^{T}\boldsymbol{u}$. This leads to a contradiction with the above fact that $\tilde{\boldsymbol{s} }^{*}$ is a solution to problem (47), and thus s ^∗ is a solution to problem (43). □

Finally, we prove Lemma 3.6.

Lemma 3.6

Let the sequences {x _k } and {ρ _k } be generated by Algorithm  1. If $\boldsymbol{x}_{k}\notin\tilde{R }_{\hat{p}}^{m}$ and $\rho_{k}\leq\frac{1}{10}$ for some index k, then there exists an index k ₀>k such that $\rho_{k'}>\frac{1}{10}$ for all k′≥k ₀.

Proof

Assume by contradiction that for some k we have $\rho_{k'}\leq\frac{1}{10}$ for all k′≥k. By Eqs. (10), (28) and the fact that $Q_{k'}(\boldsymbol{0})= \hat{p}(\boldsymbol{x}_{k'})$ we obtain

$$\begin{aligned} |\rho_{k'}-1| =& \frac{|\hat{p}(\boldsymbol{x}_{k'}+\boldsymbol{s}_{k'})-\hat{p}(\boldsymbol {x}_{k'})-[Q_{k'}(\boldsymbol{s}_{k'})-Q_{k'}(\boldsymbol{0})]|}{Q_{k'}( \boldsymbol{s}_k)-Q_{k'}(\boldsymbol{0})} \\ =& \frac{|\hat{p}(\boldsymbol{x}_{k'}+\boldsymbol{s}_{k'})-Q_{k'}(\boldsymbol{ s}_{k'})|}{\tilde{Q}_{k'}(\tilde{\boldsymbol{s}}_{k'})} \end{aligned}$$

(51)

for all k′. On the other hand, by Lemma 3.2 the superlevel set $\mathcal{L}_{\hat{p}(\boldsymbol{x})}$ is compact for any $\boldsymbol{x}\in\mathbb{R}^{d}$. Thus, since $\hat{p}$ is a C ^∞-function, we can choose a point $\boldsymbol{z}\in\mathbb{R}^{d}$ such that the Hessian $\nabla^{2}\hat{p}$ is locally Lipschitz-continuous with some Lipschitz constant L>0 on the compact set $\mathcal{L}_{\hat{p}(\boldsymbol{ z})}$ whose interior contains x _k . Hence, for the numerator of Eq. (51) we obtain the Taylor series estimate (see e.g. [14], Theorem 1.1)

$$ \bigl|\hat{p}(\boldsymbol{x}_{k'}+ \boldsymbol{s}_{k'})-Q_{k'}(\boldsymbol{s}_{k'} )\bigr| \leq \frac{1}{6}L\|\boldsymbol{s}_{k'}\|^3 $$

(52)

that holds when $\boldsymbol{x}_{k'}+\boldsymbol{s}_{k'}\in\mathcal{L}_{\hat{ p}(\boldsymbol{z})}$. On the other hand, by Lemma 3.3 Eq. (31) holds, and thus for the denominator of Eq. (51) we have

$$ \tilde{Q}_{k'}(\tilde{\boldsymbol{s}}_{k'})= \frac{1}{2}\bigl(\|\boldsymbol{R}_{k'}\tilde{ \boldsymbol{s}}_{k'}\|^2+\kappa_{k'} \varDelta_{k'}^2\bigr)\geq \frac{1}{2} \kappa_{k'}\varDelta_{k'}^2 $$

(53)

for all k′≥k with some $\boldsymbol{R}_{k'}\in\mathbb{R}^{(d-m)\times (d-m)}$.

By the assumption that $\rho_{k'}\leq\frac{1}{10}$ for all k′≥k, we have lim _k′→∞ Δ _k′=0 by the updating rules (11) and x _k′=x _k for all k′≥k. Thus, there exists k ₀≥k such that $\boldsymbol{x}_{ k'}+\boldsymbol{s}_{k'}\in\mathcal{L}_{\hat{p}(\boldsymbol{z})}$ for all k′≥k ₀, which implies that inequality (52) holds for all k′≥k ₀. Then substituting inequalities (52) and (53) into Eq. (51) and noting that ∥s _k′∥≤Δ _k′ for all k′ yields

$$ |\rho_{k'}-1|\leq \frac{L\|\boldsymbol{s}_{k'}\|^3}{3\kappa_{k'}\varDelta_{k'}^2} \leq \frac{L\varDelta_{k'}}{3\kappa_{k'}} $$

(54)

for all k′≥k ₀.

The remainder of the proof is divided into two cases. If λ _m+1(x _k )>0, then for all k′>k we have κ _k′≥λ _m+1(x _k′)=λ _m+1(x _k )>0 by condition (27) and the fact that x _k′=x _k for all k′≥k. Hence, by inequality (54) and the limiting value lim _k′→∞ Δ _k′=0 we obtain that

$$ \lim_{k'\to\infty}|\rho_{k'}-1|\leq \lim _{k'\to\infty}\frac{L\varDelta_{k'}}{3\kappa_{k'}}\leq \lim_{k'\to\infty} \frac{L\varDelta_{k'}}{3\lambda_{m+1}(\boldsymbol{x}_k)}=0, $$

which leads to contradiction with the assumption that $\rho_{k'}\leq\frac{1}{ 10}$ for all k′≥k.

On the other hand, when λ _m+1(x _k )≤0, it suffices to consider the case when lim _κ→0∥s _k (κ)∥>0, where

$$ \bigl\|\boldsymbol{s}_k(\kappa)\bigr\|= \Biggl\{\sum _{i=m+1}^d\frac{[\nabla\hat{p}(\boldsymbol{x}_k)^T \boldsymbol{v}_i(\boldsymbol{x}_k)]^2}{[\lambda_i(\boldsymbol{x}_k) -\kappa]^2} \Biggr\}^{\frac{1}{2}} $$

corresponds to Eq. (18). Otherwise, if λ _m+1(x _k )≤0 and lim _κ→0∥s _k (κ)∥=0, then $\nabla\hat{p}(\boldsymbol{x}_{k})^{T}\boldsymbol{v}_{i}( \boldsymbol{x}_{k})=0$ for all i=m+1,m+2,…,d, and thus $\boldsymbol{x}_{k} \in\tilde{R}_{\hat{p}}^{m}$ (and Algorithm 1 has already terminated by conditions (12)). Since x _k′=x _k for all k′≥k by the assumption that $\rho_{k' }\leq\frac{1}{10}$ for all k′≥k, we observe that ∥s _k′(κ)∥=∥s _k (κ)∥ for all κ and k′≥k. So, if λ _m+1(x _k )≤0 and lim _κ→0∥s _k (κ)∥>0, there exists k ₁≥k such that lim _κ→0∥s _k′(κ)∥=lim _κ→0∥s _k (κ)∥>Δ _k′>0 for all k′≥k ₁ since lim _k′→∞ Δ _k′=0 by the updating rules (11). Thus, since the function ∥s _k′(κ)∥=∥s _k (κ)∥ is continuous and monotoneously decreasing in the interval ]0,∞[, for all k′≥k ₁ the equation ∥s _k′(κ)∥=Δ _k has a unique solution lying in the interval ]0,∞[. By these properties, if we denote such a solution by $\kappa^{*}_{k'}$, we have $\lim_{k'\to\infty}\kappa^{*}_{k'}= \infty$ since lim _k′→∞ Δ _k′=0. As stated in Sect. 3.2, at each iteration k′≥k ₁ Algorithm 2 generates κ _k′ as such a solution. From inequality (54) we then conclude that lim _k′→∞|ρ _k′−1|=0, which again leads to contradiction with the assumption that $\rho_{k'}\leq\frac{1}{10}$ for all k′≥k. □