iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s10589-010-9363-1
A trust region algorithm with adaptive cubic regularization methods for nonsmooth convex minimization | Computational Optimization and Applications Skip to main content
Springer Nature Link
Log in

A trust region algorithm with adaptive cubic regularization methods for nonsmooth convex minimization

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

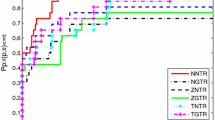
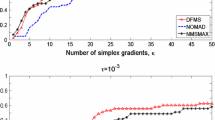
Abstract

By using the Moreau-Yosida regularization and proximal method, a new trust region algorithm is proposed for nonsmooth convex minimization. A cubic subproblem with adaptive parameter is solved at each iteration. The global convergence and Q-superlinear convergence are established under some suitable conditions. The overall iteration bound of the proposed algorithm is discussed. Preliminary numerical experience is reported.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Birge, J.R., Qi, L., Wei, Z.: A general approach to convergence properties of some methods for nonsmooth convex optimization. Appl. Math. Optim. 38, 141–158 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  2. Birge, J.R., Qi, L., Wei, Z.: Convergence analysis of some methods for minimizing a nonsmooth convex function. J. Optim. Appl. 97, 357–383 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bonnans, J.F., Gilbert, J.Ch., Lemaréchal, C., Sagastizábal, C.A.: A family of variable metric proximal methods. Math. Program. 68, 15–47 (1995)

    MATH  Google Scholar 

  4. Cartis, C., Gould, N.I.M., Toint, P.L.: Adaptive cubic regularisation methods for unconstrained optimization. Part I: motivation, convergence and numerical results. Math. Program. (2009). doi:10.1007/s10107-009-0286-5

    Google Scholar 

  5. Cartis, C., Gould, N.I.M., Toint, P.L.: Adaptive cubic regularisation methods for unconstrained optimization. Part II: worst-case function- and derivative-evaluation complexity. Math. Program. (2010). doi:10.1007/s10107-009-0337-y

    Google Scholar 

  6. Clark, F.H.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)

    Google Scholar 

  7. Conn, A.R., Gould, N.I.M., Toint, P.L.: Trust-Region Methods. SIAM, Philadelphia (2000)

    Book  MATH  Google Scholar 

  8. Correa, R., Lemaréchal, C.: Convergence of some algorithms for convex minimization. Math. Program. 62, 261–275 (1993)

    Article  MATH  Google Scholar 

  9. Dennis, J.E. Jr, Li, S.B., Tapia, R.A.: A unified approach to global convergence of trust region methods for nonsmooth optimization. Math. Program. 68, 319–346 (1995)

    MathSciNet  MATH  Google Scholar 

  10. Fukushima, M.: A descent algorithm for nonsmooth convex optimization. Math. Program. 30, 163–175 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  11. Fukushima, M., Qi, L.: A global and superlinearly convergent algorithm for nonsmooth convex minimization. SIAM J. Optim. 6, 1106–1120 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hiriart-Urruty, J.B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms ∏. Springer, Berlin (1993)

    Google Scholar 

  13. Kiwiel, K.C.: Proximal level bundle methods for convex nondifferentiable optimization, saddle-point problems and variational inequalities. Math. Program. 69, 89–109 (1995)

    MathSciNet  MATH  Google Scholar 

  14. Lemaréchal, C., Sagastizábal, C.: Practical aspects of the Moreau-Yosida regularization: theoretical preliminaries. SIAM J. Optim. 7, 367–385 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  15. Lukšan, L., Vlček, J.: Globally convergent variable metric method for convex nonsmooth unconstrained minimization. J. Optim. Theory Appl. 102, 593–613 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lukšan, L., Vlček, J.: Test problems for nonsmooth unconstrained and linearly constrained optimization, Technical report V-798, Institute of Computer Science, Academy of Sciences of the Czech Republic, Prague, Czech Republic (2000)

  17. Meng, F., Zhao, G.: On second-order properties of the Moreau-Yosida regularization for constrained nonsmooth convex programs. Numer. Funct. Anal. Optim. 25, 515–529 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  18. Meng, F., Sun, D., Zhao, G.: Semismoothness of solutions to generalized equations and the Moreau-Yosida regularization. Math. Program. 104, 561–581 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Meng, F., Zhao, G., Goh, M., et al.: Lagrangian-dual functions and Moreau-Yosida regularization. SIAM J. Optim. 19, 39–61 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Nestero, Y.: Accelerating the cubic regularization of Newton’s methods on convex problems. Math. Program. 112, 159–181 (2008)

    Article  MathSciNet  Google Scholar 

  21. Nesterov, Y., Polyak, B.T.: Cubic regularization of Newton’s method and its global performance. Math. Program. 108, 177–205 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  22. Pang, J.S., Qi, L.: A global convergent Newton methods for convex SC 1 minimization problems. J. Optim. Theory Appl. 85, 633–648 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  23. Qi, L.: Convergence analysis of some algorithms for solving nonsmooth equations. Math. Oper. Res. 18, 227–244 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  24. Qi, L., Sun, J.: A nonsmooth version of Newton’s method. Math. Program. 58, 353–367 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  25. Qi, L., Sun, J.: A trust region algorithm for minimization of locally Lipschitzian functions. Math. Program. 66, 25–43 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  26. Qi, L., Womersley, R.S.: An SQP algorithm for extended linear problems in stochastic programming. Ann. Oper. Res. 56, 251–285 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  27. Schramm, H., Zowe, J.: A version of the bundle idea for minimizing a nonsmooth function: conceptual idea, convergence analysis, numerical results. SIAM J. Optim. 2, 121–152 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wei, Z., Qi, L.: Convergence analysis of a proximal Newton method. Numer. Funct. Anal. Optim. 17, 463–472 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wei, Z., Qi, L., Birge, J.R.: A new methods for nonsmooth convex optimization. J. Inequal. Appl. 2, 157–179 (1998)

    MathSciNet  MATH  Google Scholar 

  30. Zhang, L.: A new trust region algorithm for nonsmooth convex minimization. Appl. Math. Comput. 193, 135–142 (2007)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Information Science, Guangxi University, Nanning, Guangxi, China

    Sha Lu & Zengxin Wei

  2. School of Mathematical Science, Guangxi Teachers Education University, Nanning, Guangxi, China

    Sha Lu

  3. School of Mathematical Sciences, Guangxi Normal University, Guilin, Guangxi, China

    Lue Li

Authors
  1. Sha Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zengxin Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lue Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sha Lu.

Additional information

This work is supported by the Chinese NSF grants 10761001 and the Scientific Research Foundation of Guangxi University (Grant No. X081082).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lu, S., Wei, Z. & Li, L. A trust region algorithm with adaptive cubic regularization methods for nonsmooth convex minimization. Comput Optim Appl 51, 551–573 (2012). https://doi.org/10.1007/s10589-010-9363-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-010-9363-1

Keywords

Search

Navigation