Abstract
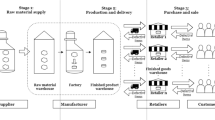
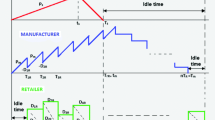
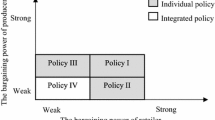
This paper presents a production inventory system with a manufacturer-retailer supply chain dealing with the non-instantaneous deteriorating products. The two-level supply chain model is analyzed with shortage and without shortage, considering the impact of business strategies in different sectors on the collaborating market system. Firstly, the integrated system and then the decentralized system under a retail fixed-mark-up strategy are studied. Further, we show that the retailer offers a fixed-mark-up policy as a signal to the manufacturer to resolve the gaming between channel members of the supply chain. This study’s prime objective is to determine the optimal retail price, wholesale price, and inventory schedules to maximize the overall supply chain’s profit. An analytical method is used to optimize the selling price and various time-length for maximum profit. The model is demonstrated through two numerical examples, and sensitivity analysis is conducted to study the behavior of parameters. It is observed from the numerical study that the supply chain system without shortage is beneficial compared to the shortage permitted supply chain. Manufacturer profit is improved after using RFM contract in contrast with integrate system.










Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bardhan S, Pal H, Giri BC (2019) Optimal replenishment policy and preservation technology investment for a non-instantaneous deteriorating item with stock-dependent demand. Oper Res 19(2):347–368
Barman A, Das R, De PK (2020) An analysis of retailer’s inventory in a two-echelon centralized supply chain co-ordination under price-sensitive demand. SN Applied Sciences 2(12):1–15
Boyacı T, Gallego G (2002) Coordinating pricing and inventory replenishment policies for one wholesaler and one or more geographically dispersed retailers. Int J Prod Econ 77(2):95–111
Catan T, Trachtenberg JA (2012) Talks quicken over e-book pricing. The Wall Street Journal
Chakraborty A, Mandal P (2021) Channel efficiency and retailer tier dominance in a supply chain with a common manufacturer. Eur J Oper Res
Chakraborty D, Garai T, Jana DK, Roy TK (2017) A three-layer supply chain inventory model for non-instantaneous deteriorating item with inflation and delay in payments in random fuzzy environment. J Ind Prod Eng 34(6):407–424
Chan CK, Wong WH, Langevin A, Lee Y (2017) An integrated production-inventory model for deteriorating items with consideration of optimal production rate and deterioration during delivery. Int J Prod Econ 189:1–13
Chang CT, Teng JT, Goyal SK (2010) Optimal replenishment policies for non-instantaneous deteriorating items with stock-dependent demand. Int J Prod Econ 123(1):62–68
Chen X, Yang H, Wang X, Choi TM (2020) Optimal carbon tax design for achieving low carbon supply chains. Ann Oper Res: 1–28
Chung KJ, Cárdenas-Barrón LE, Ting PS (2014) An inventory model with non-instantaneous receipt and exponentially deteriorating items for an integrated three layer supply chain system under two levels of trade credit. Int J Prod Econ 155:310–317
Das SC, Manna AK, Rahman MS, Shaikh AA, Bhunia AK (2021) An inventory model for non-instantaneous deteriorating items with preservation technology and multiple credit periods-based trade credit financing via particle swarm optimization. Soft Comput 25(7):5365–5384
Dye CY (2013) The effect of preservation technology investment on a non-instantaneous deteriorating inventory model. Omega 41(5):872–880
Geetha K, Uthayakumar R (2010) Economic design of an inventory policy for non-instantaneous deteriorating items under permissible delay in payments. J Comput Appl Math 233(10):2492–2505
Ghare P (1963) A model for an exponentially decaying inventory. J ind Engng 14:238–243
Ghiami Y, Williams T (2015) A two-echelon production-inventory model for deteriorating items with multiple buyers. Int J Prod Econ 159:233–240
Ghoreishi M, Mirzazadeh A, Weber GW (2014) Optimal pricing and ordering policy for non-instantaneous deteriorating items under inflation and customer returns. Optimization 63(12):1785–1804
Giri B, Roy B, Maiti T (2017) Coordinating a three-echelon supply chain under price and quality dependent demand with sub-supply chain and rfm strategies. Appl Math Model 52:747–769
Goyal S, Gunasekaran A (1995) An integrated production-inventory-marketing model for deteriorating items. Comput Ind Eng 28(4):755–762
He Y, Wang SY, Lai KK (2010) An optimal production-inventory model for deteriorating items with multiple-market demand. Eur J Oper Res 203(3):593–600
Huang YS, Ho JW, Jian HJ, Tseng TLB (2021) Quantity discount coordination for supply chains with deteriorating inventory. Comput Ind Eng 152:106987
Jaggi CK, Tiwari S, Goel SK (2017) Credit financing in economic ordering policies for non-instantaneous deteriorating items with price dependent demand and two storage facilities. Ann Oper Res 248 (1-2):253–280
Khakzad A, Gholamian MR (2020) The effect of inspection on deterioration rate: An inventory model for deteriorating items with advanced payment. J Clean Prod 254:120117
Li G, He X, Zhou J, Wu H (2019) Pricing, replenishment and preservation technology investment decisions for non-instantaneous deteriorating items. Omega 84:114–126
Linh CT, Hong Y (2009) Channel coordination through a revenue sharing contract in a two-period newsboy problem. Eur J Oper Res 198(3):822–829
Liu Ml, Li Zh, Anwar S, Zhang Y (2021) Supply chain carbon emission reductions and coordination when consumers have a strong preference for low-carbon products. Environ Sci Pollut Res: 1–15
Maihami R, Kamalabadi IN (2012) Joint pricing and inventory control for non-instantaneous deteriorating items with partial backlogging and time and price dependent demand. Int J Prod Econ 136(1):116–122
Maihami R, Karimi B (2014) Optimizing the pricing and replenishment policy for non-instantaneous deteriorating items with stochastic demand and promotional efforts. Comput Oper Res 51:302–312
Mashud AHM, Roy D, Daryanto Y, Chakrabortty RK, Tseng ML (2021) A sustainable inventory model with controllable carbon emissions, deterioration and advance payments. J Clean Prod 296:126608
Mishra U, Tijerina-Aguilera J, Tiwari S, Cárdenas-Barrón LE (2021) Production inventory model for controllable deterioration rate with shortages. RAIRO-Operations Research 55:S3– S19
Mrázová M., Neary JP (2014) Together at last: trade costs, demand structure, and welfare. American Economic Review 104(5):298–303
Nie J, Wang Q, Shi C, Zhou Y (2021) The dark side of bilateral encroachment within a supply chain. J Oper Res Soc: 1–11
Pal B, Sana SS, Chaudhuri K (2012) Three-layer supply chain–a production-inventory model for reworkable items. Appl Math Comput 219(2):530–543
Palanivel M, Uthayakumar R (2015) Finite horizon eoq model for non-instantaneous deteriorating items with price and advertisement dependent demand and partial backlogging under inflation. Int J Syst Sci 46 (10):1762–1773
Sana SS (2011) A production-inventory model of imperfect quality products in a three-layer supply chain. Decision Support Systems 50(2):539–547
Sarkar B (2013) A production-inventory model with probabilistic deterioration in two-echelon supply chain management. Appl Math Model 37(5):3138–3151
Sarkar S, Tiwari S, Wee HM, Giri B (2020) Channel coordination with price discount mechanism under price-sensitive market demand. Int Trans Oper Res 27(5):2509–2533
Taghizadeh-Yazdi M, Farrokhi Z, Mohammadi-Balani A (2020) An integrated inventory model for multi-echelon supply chains with deteriorating items: a price-dependent demand approach. J Ind Prod Eng 37(2-3):87–96
Taleizadeh AA, Noori-daryan M (2016) Pricing, manufacturing and inventory policies for raw material in a three-level supply chain. Int J Syst Sci 47(4):919–931
Tat R, Taleizadeh AA, Esmaeili M (2015) Developing economic order quantity model for non-instantaneous deteriorating items in vendor-managed inventory (vmi) system. Int J Syst Sci 46(7):1257–1268
Valliathal M, Uthayakumar R (2011) Optimal pricing and replenishment policies of an eoq model for non-instantaneous deteriorating items with shortages. Int J Adv Manuf Technol 54(1-4):361–371
Wee HM (1993) Economic production lot size model for deteriorating items with partial back-ordering. Comput Ind Eng 24(3):449–458
Wu KS, Ouyang LY, Yang CT (2006) An optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand and partial backlogging. Int J Prod Econ 101(2):369–384
Wu KS, Ouyang LY, Yang CT (2009) Coordinating replenishment and pricing policies for non-instantaneous deteriorating items with price-sensitive demand. Int J Syst Sci 40(12):1273– 1281
Wu W, Zhang Q, Liang Z (2020) Environmentally responsible closed-loop supply chain models for joint environmental responsibility investment, recycling and pricing decisions. J Clean Prod 259:120776
Yang PC, Wee HM (2003) An integrated multi-lot-size production inventory model for deteriorating item. Comput Oper Res 30(5):671–682
Zhang J, Liu G, Zhang Q, Bai Z (2015) Coordinating a supply chain for deteriorating items with a revenue sharing and cooperative investment contract. Omega 56:37–49
Zhang L, Wang J, You J (2015) Consumer environmental awareness and channel coordination with two substitutable products. Eur J Oper Res 241(1):63–73
Zhou W, Pu Y, Dai H, Jin Q (2017) Cooperative interconnection settlement among ISPs through NAP. Eur J Oper Res 256(3):991–1003
Acknowledgements
Authors of this paper express gratitude to the Hon’ble reviewers for their valuable comments. After addressing and incorporating these comments, the quality of the paper definitely enhanced.
Funding
Only the first author is financially supported by senior research fellowship from MHRD, Govt. of India.
Author information
Authors and Affiliations
Contributions
Abhijit Barman: conceptualization, methodology, validation, writing – original draft. Rubi Das: formal analysis, visualization, writing – review & editing. Pijus Kanti De: supervision, resources.
Corresponding author
Ethics declarations
Conflict of Interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Proof of Lemma 1
Taking the first order and second order partial derivatives of TPSC in (32) with respect to p gives
and,
Now, \(\frac {\partial ^{2} TP_{SC} }{\partial p^{2}}< 0\) if
holds. □
Proof of Lemma 2
Taking the first and second order partial derivatives of TPSC in (32) with respect to T gives
and,
Now, \(\frac {\partial ^{2} TP_{SC} }{\partial T^{2}}< 0\) if,
holds. □
Proof of Theorem 1
To verify the optimality of the solution obtained from (35) and (36), we have calculated the Hessian matrix (HModel1−A) and show that the hessian matrix is negative definite. i.e., det(HModel1−A) > 0.
Here,
Here, the expression
The determinant of the hessian matrix are evaluated by
Due to complexities of the expressions in Hessian matrix HModel1−A, the concavity condition of TPSC with respect to (p,T) is hardly verified by mathematical derivation, but in numerically conducted in Section (7) has shown its concavity (see Fig. (5a)). □
Appendix B
Proof of Lemma 3
Taking the first and second order partial derivatives of TPSC in (33) with respect to p gives
and,
Clearly, \(\frac {\partial ^{2} TP_{SC} }{\partial p^{2}} < 0\). Since, we have considered a positive inventory of the retailer for Dr > Dc. □
Proof of Lemma 4
Taking the first and second order derivative of TPSC in (33) with respect to T, we have
and,
Now, \(\frac {\partial ^{2} TP_{SC}}{\partial T^{2}}<0\) if
holds. □
Proof of Theoram 2
To verify the optimality of the solution obtained from (37), (38), we have calculated the hessian matrix of the profit functions is negative definite i.e. if \(\frac {\partial ^{2} TP_{SC} }{\partial p^{2}}\frac {\partial ^{2} TP_{SC} }{\partial T^{2}}- \{ \frac {\partial ^{2} TP_{SC}}{\partial p\partial T} \}^{2}>0\)
Here,
High complexity of the expressions in Hessian matrix HModel1−B, the concavity condition of TPSC with respect to (p,T) is difficult to verify by mathematical derivation, but numerically in Section (7) has shown its concavity (see Fig. (5b)). □
Rights and permissions
About this article
Cite this article
Barman, A., Das, R. & De, P.K. An analysis of optimal pricing strategy and inventory scheduling policy for a non-instantaneous deteriorating item in a two-layer supply chain. Appl Intell 52, 4626–4650 (2022). https://doi.org/10.1007/s10489-021-02646-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-021-02646-2