iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s10479-005-2247-6
Competition and Cooperation in Non-Centralized Linear Production Games | Annals of Operations Research Skip to main content
Springer Nature Link
Log in

Competition and Cooperation in Non-Centralized Linear Production Games

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

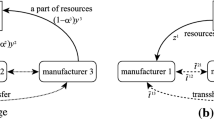
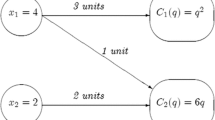
In this paper we analyze how to improve the benefits of n producers when: (1) each producer i faces a linear production problem given by max {c i x i:A i x i≤ b i,x i 0}, and (2) maintaining the production capabilities of each producer is mandatory. In order to maximize the benefits, the producers decide to trade their resources while ensuring their initial individual gains. We study the games which describe this non-centralized linear production situation when players do not cooperate (section two), when players cooperate and side payments are possible (section three), and when players cooperate and side payments are not possible (section four).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Curiel, I., J. Derks, and S. Tijs. (1989). “On Balanced Games and Games with Committee Control.” OR Spektrum 11, 83–88.

    Article  Google Scholar 

  • Feltkamp, V., A. van den Nouweland, P. Borm, M. Koster, and S. Tijs. (1993). “Linear Production with Transport of Products, Resources, and Technology.” ZOR 38, 153–162.

    Google Scholar 

  • Fernández, F.R., M.G. Fiestras, I. García-Jurado, and J.Puerto. (2003). “On the Allocation of Excesses of Resources inLinear Production Problems.” In U. Leopold-Wildburger, F. Rendl,and G. Wäscher (eds.), Operations Research Proceedings 2002. Heidelberg: Springer-Verlag, pp. 465–470.

    Google Scholar 

  • Granot, D. (1986). “A Generalized Linear Production Model: A Unifying Model.” Mathematical Programming 34, 212–222.

    Article  Google Scholar 

  • Kalai, E. and E. Zemel (1982). “Generalized Network Problems Yielding Totally Balanced Games.” Operations Research 30, 998–1008.

    Article  Google Scholar 

  • Owen, G. (1975). “The Core of Linear Production Games.” Mathematical Programming 9, 358–370.

    Article  Google Scholar 

  • Owen, G. (1995). Game Theory. San Diego: Academic Press.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Facultad de Matemáticas, Universidad de Sevilla, 41012, Sevilla, Spain

    Francisco Ramón Fernández

  2. Facultade de Económicas, Universidade de Vigo, 36200, Vigo, Spain

    MarÍa Gloria Fiestras-Janeiro

  3. Facultade de Matemáticas, Universidade de Santiago de Compostela, 15782, Santiago de Compostela, Spain

    Ignacio GarcÍa-Jurado

  4. Dep. Estadistica e Investigacion Operative, Facultad de Matemáticas, Universidad de Sevilla, 41012, Sevilla, Spain

    Justo Puerto

Authors
  1. Francisco Ramón Fernández
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. MarÍa Gloria Fiestras-Janeiro
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ignacio GarcÍa-Jurado
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Justo Puerto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Francisco Ramón Fernández.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fernández, F.R., Fiestras-Janeiro, M.G., GarcÍa-Jurado, I. et al. Competition and Cooperation in Non-Centralized Linear Production Games. Ann Oper Res 137, 91–100 (2005). https://doi.org/10.1007/s10479-005-2247-6

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-005-2247-6

Keywords

Search

Navigation