iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s10472-010-9222-x
A new stochastic approach for solution of Riccati differential equation of fractional order | Annals of Mathematics and Artificial Intelligence Skip to main content
Springer Nature Link
Log in

A new stochastic approach for solution of Riccati differential equation of fractional order

  • Published:
Annals of Mathematics and Artificial Intelligence Aims and scope Submit manuscript

Abstract

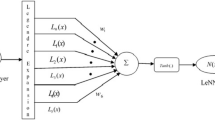
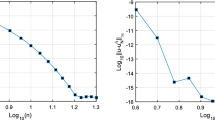
In this article, a stochastic technique has been developed for the solution of nonlinear Riccati differential equation of fractional order. Feed-forward artificial neural network is employed for accurate mathematical modeling and learning of its weights is made with heuristic computational algorithm based on swarm intelligence. In this scheme, particle swarm optimization is used as a tool for the rapid global search method, and simulating annealing for efficient local search. The scheme is equally capable of solving the integer order or fractional order Riccati differential equations. Comparison of results was made with standard approximate analytic, as well as, stochastic numerical solvers and exact solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Reid, W.T.: Riccati Differential Equations. Mathematics in Science and Engineering, vol. 86. Academic Press, New York (1972)

    Google Scholar 

  2. Anderson, B.D., Moore, J.B.: Optimal Control-linear Quadratic Methods. Prentice-Hall, New Jersey (1999)

    Google Scholar 

  3. Bittanti, S.: History and prehistory of the Riccati equation. In: Proc. 35th IEEE Conf. on Decision and Control, pp. 1599–1604. Kobe, Japan (1996)

    Google Scholar 

  4. Goldstine, H.H.: A History of the Calculus of Variations from the 17th Through the 19th Century. Springer-Verlag (1980). ISBN: 0387905219

  5. Mitter, S.K.: Filtering and stochastic control: a historical perspective. IEEE Control Syst. Mag. 16(3), 67–76 (1996)

    Article  Google Scholar 

  6. Kravchenko, V.V.: Applied Pseudoanalytic Function Theory, Frontiers in Mathematics. Birkhäuser, Verlag AG, Basel . Boston . Berlin (2009). ISBN: 978-3-0346-0003-3

  7. Conte, R., Musette, M.: Link between solitary waves and projective Riccati Equations. J. Phys. A. Math. Gen. 25, 5609–5623 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  8. Wu, J.L., Chen, G.H.: A new operational approach for solving Fractional Calculus and Fractional differential equations numerically. In: Proceeding (397) Software Engineering and Applications (2003)

  9. Diethelm, K., Ford, J.M., Ford, N.J., Weilbeer, W.: Pitfalls in fast numerical solvers for fractional differential equations. J. Comput. Appl. Math. 186, 482–503 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Mainardi, F., Pagnini, G., Gorenflo, R.: Some aspects of fractional diffusion equations of single and distributed orders. Appl. Math. Comput. 187(1), 295–305 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  11. Geng, F., Lin, Y., Cui, M.: A piecewise variational iteration method for Riccati differential equations. Comput. Math. Appl. 58, 2518–2522 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Li, C., Wang, Y.: Numerical algorithm based on Adomian decomposition for fractional differential equations. Comput. Math. Appl. 57, 1672–1681 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  13. Abbasbandy, S.: A new application of He’s variational iteration method for quadratic Riccati differential equation by using Adomian’s polynomials. J. Comput. Appl. Math. 207(1), 59–63 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Galeone, L., Garrappa, R.: Fractional Adams-Moulton methods. Math. Comput. Simulat. 79(4), 1358–1367 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  15. Tsoulos, L.G., Gavrilis, D., Glavas, E.: Solving differential equations with constructed neural networks. Neurocomputing 72, 2385–2391 (2009)

    Article  Google Scholar 

  16. Malek, A., Beidokhti, R.S.: Numerical solution for high order differential equations using a hybrid neural network-optimization method. Appl. Math. Comput. 183(1), 260–271 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. Junaid, A., Raja, M.A.Z., Qureshi, I.M.: Evolutionary computing approach for the solution of initial value problem in ordinary differential equation. Proceeding WASET 55, 578–581 (2009)

    Google Scholar 

  18. Yazdi, H.S., Pourreza, R.: Unsupervised adaptive neural-fuzzy inference system for solving differential equations. Appl. Soft Comput. 10(1), 267–275 (2010)

    Article  Google Scholar 

  19. Angeline, P.: Evolutionary Optimization versus Particle Swarm Optimization: Philosophy and Performance Differences. Evolutionary Programming. Lecture Notes in Computer Science, vol. 1447, pp. 601–610. Springer (1998)

  20. Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York (1974)

    MATH  Google Scholar 

  21. Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)

    MATH  Google Scholar 

  22. Anatoly, A.K., Srivastava, H.M., Trujillo, J.J.: Theory and Application of Fractional Differential Equations. North-Holl. Math. Stud., vol. 204. Elsevier (2006)

  23. Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)

    MATH  Google Scholar 

  24. Caputo, M.: Linear models of dissipation whose Q is almost frequency independent. Part II. J. Roy. Astr. Soc. 13, 529–539 (1967)

    Google Scholar 

  25. Diethelm, K., Ford, N.J.: Multi-order fractional differential equations and their numerical solution. Appl. Math. Comput. 154, 621–640 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  26. Mainardi, F., Gorenflo, R.: The Mittag-Leffler function in the Riemann-Liouville fractional calculus. In: Kilbas, A.A. (ed.) Proceedings International Conference Dedicated to the Memory of Academician F. D. Gakhov; Held in Minsk, pp. 215–225. Beloruss Gos. Univ., Minsk (1996)

    Google Scholar 

  27. Beidokhti, R.S., Malek, A.: Solving initial-boundary value problems for systems of partial differential equations using neural networks and optimization techniques. J. Franklin Inst. 346(9), 898–913 (2009)

    Article  MathSciNet  Google Scholar 

  28. Parisi, D.R., Mariani, M.C., Laborde, M.A.: Solving differential equations with unsupervised neural networks. Chem. Eng. Process. 42(8–9), 715–721 (2003)

    Article  Google Scholar 

  29. He, S., Reif, K., Unbehauen, R.: Multilayer neural networks for solving a class of partial differential equations. Neural Netw. 13(3), 385–396 (2000)

    Article  Google Scholar 

  30. Kumaresan, N., Balasubramaniam, P.: Optimal control for stochastic linear quadratic singular system using neural networks. J. Process Control 19(3), 482–488 (2009)

    Article  MATH  Google Scholar 

  31. Eberhart, R.C., Shi, Y.: Comparison between genetic algorithms and particle swarm optimization. In: Porto, V.W. (ed.) Evolutionary Programming. Lecture Notes in Computer Science, vol. 1447, pp. 611–616. Springer, Heidelberg (1998)

    Chapter  Google Scholar 

  32. Kennedy, J., Eberhart, R.C.: Particle swarm optimization. In: Proc. IEEE International Conference on Neural Networks, vol. 4, pp. 1942–1948 (1995)

  33. Eberhart, R., Kennedy, J.: A new optimizer using particle swarm theory. In: Proc. of the 6th Int. Symp. On Micro Machine and Human Science, pp. 39–43. IEEE Service Center, Piscataway, NJ (1995)

    Chapter  Google Scholar 

  34. Berro, A., Marie-Sainte, S.L., Ruiz-Gazen, A.: Genetic algorithms and particle swarm optimization for exploratory projection pursuit. Ann. Math. Artif. Intell. (2010). doi:10.1007/s10472-D10-9211-D

  35. Inthachot, M.I., Supratid, S.: A multi-subpopulation particle swarm optimization: a hybrid intelligent computing for function optimization. In: IEEE, 3rd International Conference on Natural Computation, 0-7695-2875-9/07 (2007)

  36. El-Tawil, M.A., Bahnasawi, A.A., Abdel-Naby, A.: Solving Riccati differential equation using Adomian’s decomposition method. J. Appl. Math. Comput. 157, 503–514 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  37. Momani, S., Shawagfeh, N.: Decomposition method for solving fractional Riccati differential equations. J. Appl. Math. Comput. 182, 1083–1092 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  38. Raja, M.A.Z., Khan, J.A., Qureshi, I.M.: Evolutionary computation technique for solving Riccati differential equation of arbitrary order. Proceeding WASET 58, 531–536 (2009)

    Google Scholar 

  39. Odibat, Z., Momani, S.: Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order. J. Chaos, Solitons Fractal 36(1), 167–174 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  40. Batiha, B., Noorani, M.S.M., Hashim, I.: Application of variational iteration method to general Riccati equation. Int. Math. Forum 2(56), 2759–2770 (2007)

    MathSciNet  MATH  Google Scholar 

  41. Raja, M.A.Z., Khan, J.A., Qureshi, I.M.: Evolutionary computational intelligence in solving the fractional differential equations. Part I. LNCS, vol. 5990, pp. 231–240. Springer-Verlag, Hue City (2010)

  42. Podlubny, I.: Mittag-Leffler Function. File ID 8738, Matlab Central. http://www.mathworks.com/matlabcentral/fileexchange/8738-mittag-leffler-function (2009)

  43. Weibeer, M.: Efficient Numerical Methods for Fractional Differential Equations and Their Analytical Background, Ch. 6. PhD Thesis, ISBN: 978-3-89720-846-9 (2005)

  44. Raja, M.A.Z., Khan, J.A., Qureshi, I.M.: Heuristic computational approach using swarm intelligence in solving fractional differential equations. In: Proc. GECCO (Companion), pp. 2023–2026 (2010)

  45. Raja, M.A.Z., Khan, J.A., Qureshi, I.M.: Swarm Intelligence Optimized Neural Networks for Solving Fractional Differential Equations. Accepted in International Journal of Innovative Computing, Information and Control (2010) Reference No.: IJICIC-10-03079

  46. Abbasbandy, S.: Homotopy perturbation method for quadratic Riccati differential equation and comparison with Adomians decomposition method. Appl. Math. Comput. 172, 485–490 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  47. Tan, Y., Abbasbandy, S.: Homotopy analysis method for quadratic Riccati differential equation. Commun. Nonlinear Sci. Numer. Simulat. 13, 539–546 (2008)

    Article  MATH  Google Scholar 

  48. Li, Y.: Solving a nonlinear fractional differential equation using Chebyshev wavelets. Commun. Nonlinear Sci. Numer. Simulat. (2009). doi:10.1016/j.cnsns.2009.09.020

  49. Odibat, Z., Momani, S., Erturk, V.S.: Generalized differential transform method: application to differential equations of fractional order. Appl. Math. Comput. 197, 467–477 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Engineering and Technology, Department of Electronic Engineering, International Islamic University, Islamabad, Pakistan

    Muhammad Asif Zahoor Raja & Junaid Ali Khan

  2. Department of Electronic Engineering, Air University, Islamabad, Pakistan

    Ijaz Mansoor Qureshi

Authors
  1. Muhammad Asif Zahoor Raja
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Junaid Ali Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ijaz Mansoor Qureshi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Muhammad Asif Zahoor Raja.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Raja, M.A.Z., Khan, J.A. & Qureshi, I.M. A new stochastic approach for solution of Riccati differential equation of fractional order. Ann Math Artif Intell 60, 229–250 (2010). https://doi.org/10.1007/s10472-010-9222-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10472-010-9222-x

Keywords

Mathematics Subject Classifications (2010)

Search

Navigation