Abstract
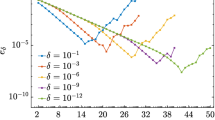
In this paper we construct an approximation to the solution x of a linear system of equations Ax=b of tensor product structure as it typically arises for finite element and finite difference discretisations of partial differential operators on tensor grids. For a right-hand side b of tensor product structure we can prove that the solution x can be approximated by a sum of  (log(ɛ)2) tensor product vectors where ɛ is the relative approximation error. Numerical examples for systems of size 1024256 indicate that this method is suitable for high-dimensional problems.
(log(ɛ)2) tensor product vectors where ɛ is the relative approximation error. Numerical examples for systems of size 1024256 indicate that this method is suitable for high-dimensional problems.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Grasedyck, L. Existence and Computation of Low Kronecker-Rank Approximations for Large Linear Systems of Tensor Product Structure. Computing 72, 247–265 (2004). https://doi.org/10.1007/s00607-003-0037-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-003-0037-z
Keywords
- Data-sparse approximation
- Sylvester equation
- low rank approximation
- Kronecker product
- high-dimensional problems