iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s00521-015-2065-y
Classifying component failures of a hybrid electric vehicle fleet based on load spectrum data | Neural Computing and Applications Skip to main content

Advertisement

Springer Nature Link
Log in

Classifying component failures of a hybrid electric vehicle fleet based on load spectrum data

Balanced random forest approaches employing uni- and multivariate decision trees

  • Predictive Analytics Using Machine Learning
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

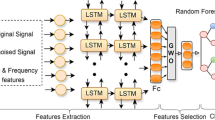
Abstract

Component failures in hybrid electric vehicles (HEV) can cause high warranty costs for car manufacturers. Hence, in order to (1) predict whether a component of the hybrid power-train of a HEV is faulty, and (2) to identify loads related to component failures, we train several random forest variants on so-called load spectrum data, i.e., the state-of-the-art data employed for calculating the fatigue life of components in fatigue analysis. We propose a parameter tuning framework that enables the studied random forest models, formed by univariate and multivariate decision trees, respectively, to handle the class imbalance problem of our dataset and to select only a small number of relevant variables in order to improve classification performance and to identify failure-related variables. By achieving an average balanced accuracy value of 85.2 %, while reducing the number of variables used from 590 to 22 variables, our results for failures of the hybrid car battery (approx. 200 faulty, 7000 non-faulty vehicles) demonstrate that especially balanced random forests using univariate decision trees achieve promising classification results on load spectrum data. Moreover, the selected variables can be related to component failures of the hybrid power-train.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Breiman L (2001) Random forests. Mach Learn 45(1):5–32. doi:10.1023/A:1010933404324

    Article  MathSciNet  MATH  Google Scholar 

  2. Breiman L, Friedman J, Olshen R, Stone C (1984) Classification and regression trees. Chapman and Hall/CRC, New York

    MATH  Google Scholar 

  3. Brodley C, Utgoff P (1995) Multivariate decision trees. Mach Learn 19(1):45–77. doi:10.1023/A:1022607123649

    MATH  Google Scholar 

  4. Köhler M, Jenne S, Pötter K, Zenner H (2012) Zählverfahren und Lastannahme in der Betriebsfestigkeit. Springer, Berlin

    Book  Google Scholar 

  5. López V, Fernández A, García S, Palade V, Herrera F (2013) An insight into classification with imbalanced data: empirical results and current trends on using data intrinsic characteristics. Inf Sci 250:113–141. doi:10.1016/j.ins.2013.07.007

    Article  Google Scholar 

  6. Genuer R, Poggi JM, Tuleau-Malot C (2010) Variable selection using random forests. Pattern Recogn Lett 31(14):2225–2236. doi:10.1016/j.patrec.2010.03.014

    Article  Google Scholar 

  7. Breiman L, Cutler A (2015) Random forests-classification description. Department of Statistics Homepage. http://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm. Accessed 15 Jan 2015

  8. Bergmeir P, Nitsche C, Nonnast J, Bargende M, Antony P, Keller U (2014) Klassifikationsverfahren zur Identifikation von Korrelationen zwischen Antriebsstrangbelastungen und Hybridkomponentenfehlern einer Hybridfahrzeugflotte. Technical report, Universität Stuttgart

  9. Vapnik VN (1995) The nature of statistical learning theory. Springer, New York

    Book  MATH  Google Scholar 

  10. Bergmeir P, Nitsche C, Nonnast J, Bargende M, Antony P, Keller U (2014) Using balanced random forests on load spectrum data for classifying component failures of a hybrid electric vehicle fleet. In: 13th international conference on machine learning and applications (ICMLA 2014), pp 397–404. doi:10.1109/ICMLA.2014.71

  11. Gusikhin O, Rychtyckyj N, Filev D (2007) Intelligent systems in the automotive industry: applications and trends. Knowl Inf Syst 12(2):147–168

    Article  Google Scholar 

  12. Buddhakulsomsiri J, Zakarian A (2009) Sequential pattern mining algorithm for automotive warranty data. Comput Ind Eng 57(1):137–147. doi:10.1016/j.cie.2008.11.006

    Article  Google Scholar 

  13. Frisk E, Krysander M, Larsson E (2014) Data-driven lead-acid battery prognostics using random survival forests. In: Proceedings of the 2nd European conference of the PHM society (PHME14)

  14. Prytz R, Nowaczyk S, Rgnvaldsson T, Byttner S (2015) Predicting the need for vehicle compressor repairs using maintenance records and logged vehicle data. Eng Appl Artif Intell 41:139–150. doi:10.1016/j.engappai.2015.02.009

    Article  Google Scholar 

  15. Lee Y, Pan J, Hathaway R, Barkey M (2011) Fatigue testing and analysis: theory and practice. Elsevier Science, Amsterdam

    Google Scholar 

  16. Kondo Y (2003) 4.10-fatigue under variable amplitude loading. In: Karihaloo IMR (ed) Comprehensive structural integrity. Pergamon, Oxford, pp 253–279

    Chapter  Google Scholar 

  17. Saha B, Goebel K (2007) Battery data set. NASA Ames Prognostics Data Repository. http://ti.arc.nasa.gov/tech/dash/pcoe/prognostic-data-repository/#battery. Accessed 12 Jan 2015

  18. Quinlan JR (1993) C4.5: programs for machine learning. Morgan Kaufmann, San Francisco

    Google Scholar 

  19. del Río S, López V, Benítez JM, Herrera F (2014) On the use of MapReduce for imbalanced big data using random forest. Inf Sci 285:112–137. doi:10.1016/j.ins.2014.03.043

    Article  Google Scholar 

  20. Hastie T, Tibshirani R, Friedman J (2009) The elements of statistical learning: data mining, inference, and prediction, 2nd edn., Springer Series in StatisticsSpringer, SpringerBerlin

    Book  MATH  Google Scholar 

  21. Liaw A, Wiener M (2002) Classification and Regression by randomForest. R News 2(3):18–22. http://CRAN.R-project.org/doc/Rnews/

  22. Schneider M, Hirsch S, Weber B, Székely G, Menze BH (2015) Joint 3-D vessel segmentation and centerline extraction using oblique Hough forests with steerable filters. Med Image Anal 19(1):220–249. doi:10.1016/j.media.2014.09.007

    Article  Google Scholar 

  23. Menze BH, Kelm BM, Splitthoff DN, Koethe U, Hamprecht FA (2011) On oblique random forests. In: Gunopulos D, Hofmann T, Malerba D, Vazirgiannis M (eds) Machine learning and knowledge discovery in databases. Springer, Berlin, pp 453–469

  24. Barros R, Cerri R, Jaskowiak P, de Carvalho A (2011) A bottom-up oblique decision tree induction algorithm. In: 11th international conference on intelligent systems design and applications (ISDA 2011), pp 450–456. doi:10.1109/ISDA.2011.6121697

  25. Murthy SK, Kasif S, Salzberg S (1994) A system for induction of oblique decision trees. J Artif Intell Res 2(1):1–32

    MATH  Google Scholar 

  26. Parfionovas A (2013) Enhancement of random forests using trees with oblique splits. Dissertation, Utah State University. http://digitalcommons.usu.edu/etd/1508. Accessed 07 Jan 2015

  27. Friedman JH, Hastie T, Tibshirani R (2010) Regularization paths for generalized linear models via coordinate descent. J Stat. Softw 33(1):1–22. http://www.jstatsoft.org/v33/i01

  28. Zou H, Hastie T (2005) Regularization and variable selection via the elastic net. J R Stat Soc Ser B 67:301–320. doi:10.1111/j.1467-9868.2005.00503.x

    Article  MathSciNet  MATH  Google Scholar 

  29. Hoerl AE, Kennard RW (2000) Ridge regression: biased estimation for nonorthogonal problems. Technometrics 42(1):80–86. doi:10.1080/00401706.2000.10485983

    Article  MathSciNet  MATH  Google Scholar 

  30. Tibshirani R (1996) Regression shrinkage and selection via the lasso. J R Stat Soc Ser B 58:267–288. doi:10.1111/j.1467-9868.2011.00771.x

    MathSciNet  MATH  Google Scholar 

  31. Truong AKY (2009) Fast growing and interpretable oblique trees via logistic regression models. Dissertation, University of Oxford. http://ora.ox.ac.uk/objects/uuid:e0de0156-da01-4781-85c5-8213f5004f10. Accessed 25 Jan 2015

  32. Martens H (2001) Reliable and relevant modelling of real world data: a personal account of the development of PLS regression. Chemom Intell Lab Syst 58(2):85–95. doi:10.1016/S0169-7439(01)00153-8

    Article  MathSciNet  Google Scholar 

  33. Wold S (2001) Personal memories of the early PLS development. Chemom Intell Lab Syst 58(2):83–84. doi:10.1016/S0169-7439(01)00152-6

    Article  MathSciNet  Google Scholar 

  34. Mevik BH, Wehrens R (2007) The pls package: principal component and partial least squares regression in R. J Stat Softw 18(2):1–24. http://www.jstatsoft.org/v18/i02

  35. Dayal BS, MacGregor JF (1997) Improved PLS algorithms. J Chemom 11(1):73–85

    Article  Google Scholar 

  36. Do TN, Lenca P, Lallich S, Pham NK (2010) Classifying very-high-dimensional data with random forests of oblique decision trees. In: Guillet F, Ritschard G, Zighed D, Briand H (eds) Advances in knowledge discovery and management, studies in computational intelligence, vol 292. Springer, Berlin, pp 39–55. doi:10.1007/978-3-642-00580-0_3

  37. Fung G, Mangasarian OL (2001) Proximal support vector machine classifiers. In: Proceedings of the seventh ACM SIGKDD international conference on knowledge discovery and data mining, ACM, New York, NY, USA, KDD ’01, pp 77–86. doi:10.1145/502512.502527

  38. Chen C, Liaw A, Breiman L (2004) Using random forest to learn imbalanced data. Technical report, Department of Statistics, University of Berkeley. http://www.stat.berkeley.edu/users/chenchao/666.pdf. Accessed 29 Dec 2014

  39. Díaz-Uriarte R, de Alvarez Andrés S (2006) Gene selection and classification of microarray data using random forest. BMC Bioinform 7(1):1–13. doi:10.1186/1471-2105-7-3

    Article  Google Scholar 

  40. Menze B, Splitthoff N (2012) obliqueRF: oblique random forests from recursive linear model splits. http://CRAN.R-project.org/package=obliqueRF. R package version 0.3

  41. Kuhn M (2008) Building predictive models in r using the caret package. J Stat Softw 28(5):1–26. http://www.jstatsoft.org/v28/i05

  42. Kuhn M, Wing J, Weston S, Williams A, Keefer C, Engelhardt A, Cooper T, Mayer Z, the R Core Team (2014) caret: Classification and regression training. http://CRAN.R-project.org/package=caret. R package version 6.0-24

  43. Brodersen K, Ong CS, Stephan K, Buhmann J (2010) The balanced accuracy and its posterior distribution. In: 20th international conference on pattern recognition (ICPR 2010), pp 3121–3124. doi:10.1109/ICPR.2010.764

  44. Dahinden C (2006) Classification with tree-based ensembles applied to the WCCI 2006 performance prediction challenge datasets. In: International joint conference on neural networks (IJCNN ’06), pp 1669–1672. doi:10.1109/IJCNN.2006.246635

  45. Kuhn M, Johnson K (2013) Applied predictive modeling. SpringerLink: Bücher, Springer. http://books.google.de/books?id=xYRDAAAAQBAJ

  46. Demšar J (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7:1–30. http://dl.acm.org/citation.cfm?id=1248547.1248548

  47. García S, Fernández A, Luengo J, Herrera F (2010) Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf Sci 180(10):2044–2064. doi:10.1016/j.ins.2009.12.010

    Article  Google Scholar 

  48. Friedman M (1937) The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J Am Stat Assoc 32(200):675–701. http://www.jstor.org/stable/2279372

  49. Friedman M (1940) A comparison of alternative tests of significance for the problem of m rankings. Ann Math Stat 11(1):86–92. http://www.jstor.org/stable/2235971

  50. Hochberg Y (1988) A sharper Bonferroni procedure for multiple tests of significance. Biometrika 75(4):800–802. doi:10.1093/biomet/75.4.800

    Article  MathSciNet  MATH  Google Scholar 

  51. Wilcoxon F (1945) Individual comparisons by ranking methods. Biom Bull 1(6):80–83

    Article  Google Scholar 

  52. Irsoy O, Yildiz OT, Alpaydin E (2012) Design and analysis of classifier learning experiments in bioinformatics: survey and case studies. IEEE/ACM Trans Comput Biol Bioinform 9(6):1663–1675

    Article  Google Scholar 

  53. Pizarro J, Guerrero E, Galindo PL (2002) Multiple comparison procedures applied to model selection. Neurocomputing 48(1–4):155–173. doi:10.1016/S0925-2312(01)00653-1

    Article  MATH  Google Scholar 

  54. Herb F (2010) Alterungsmechanismen in Lithium-Ionen-Batterien und PEM-Brennstoffzellen und deren Einfluss auf die Eigenschaften von daraus bestehenden hybrid-systemen. Dissertation, University Ulm, Faculty of Natural Sciences. http://vts.uni-ulm.de/doc.asp?id=7404. Accessed 04 Jan 2015

Download references

Acknowledgments

P. Bergmeir participates in the doctoral program “Promotionskolleg HYBRID”, funded by the Ministry for Science, Research and Arts Baden-Württemberg, Germany. For computational resources, the authors acknowledge the bwGRiD (http://www.bw-grid.de), member of the German D-Grid initiative, funded by the Ministry for Education and Research and the Ministry for Science, Research and Arts Baden-Württemberg, Germany.

Conflict of interest

The authors declare that they have no conflict of interest.

Author information

Authors and Affiliations

  1. Department of Information Technology, Esslingen University of Applied Sciences, Flandernstr. 101, 73732, Esslingen, Germany

    Philipp Bergmeir & Jürgen Nonnast

  2. Daimler AG, Mercedes-Benz Sindelfingen Plant, Bela-Barenyi-Str. 14, 71063, Sindelfingen, Germany

    Christof Nitsche

  3. Institute for Internal Combustion Engines and Automotive Engineering, University of Stuttgart, Pfaffenwaldring 12, 70569, Stuttgart, Germany

    Michael Bargende

Authors
  1. Philipp Bergmeir
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christof Nitsche
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jürgen Nonnast
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Michael Bargende
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Philipp Bergmeir.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bergmeir, P., Nitsche, C., Nonnast, J. et al. Classifying component failures of a hybrid electric vehicle fleet based on load spectrum data. Neural Comput & Applic 27, 2289–2304 (2016). https://doi.org/10.1007/s00521-015-2065-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-2065-y

Keywords

Search

Navigation