iBet uBet web content aggregator. Adding the entire web to your favor.
iBet uBet web content aggregator. Adding the entire web to your favor.



Link to original content: https://doi.org/10.1007/s00521-006-0046-x
The p-recursive piecewise polynomial sigmoid generators and first-order algorithms for multilayer tanh-like neurons | Neural Computing and Applications Skip to main content
Springer Nature Link
Log in

The p-recursive piecewise polynomial sigmoid generators and first-order algorithms for multilayer tanh-like neurons

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

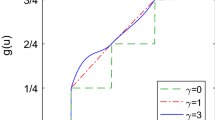
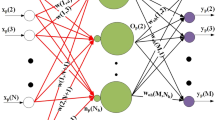
This paper demonstrates how the p-recursive piecewise polynomial (p-RPP) generators and their derivatives are constructed. The feedforward computational time of a multilayer feedforward network can be reduced by using these functions as the activation functions. Three modifications of training algorithms are proposed. First, we use the modified error function so that the sigmoid prime factor for the updating rule of the output units is eliminated. Second, we normalize the input patterns in order to balance the dynamic range of the inputs. And third, we add a new penalty function to the hidden layer to get the anti-Hebbian rules in providing information when the activation functions have zero sigmoid prime factor. The three modifications are combined with two versions of Rprop (Resilient propagation) algorithm. The proposed procedures achieved excellent results without the need for careful selection of the training parameters. Not only the algorithm but also the shape of the activation function has important influence on the training performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Haykin S (1999) Neural networks: a comprehensive foundation, 2nd edn. Prentice-Hall, Upper Saddle River

    Google Scholar 

  2. Pao YH (1989) Adaptive pattern recognition and neural networks. Addison-Wesley, Reading

    MATH  Google Scholar 

  3. Kwan HK (1992) Simple sigmoid-like activation function suitable for digital hardware implementation. IEE Electron Lett 28(15):379–1380

    Google Scholar 

  4. Zhang M, Vassiliadis S, Delgado-Frias JG (1996) Sigmoid generators for neural computing using piecewise approximation. IEEE Trans Comput 45(2):1045–1049

    Article  MATH  Google Scholar 

  5. Basterretxea K, Tarela JM, del Campo I (2002) Digital design of sigmoid approximation for artificial neural networks. IEE Electron Lett 38(1):35–37

    Article  Google Scholar 

  6. Piazza A (1992) Neural networks with digital LUT activation function. In: Proceedings of 1993 international joint conference on neural networks (IJCNN’93), vol 2, Nagoya, Japan, 25–29 October 1993

  7. Piazza A, Uncini A, Zenobi M (1992) Artificial neural networks with adaptive polynomial activation function. In: Proceedings of the international joint conference on neural networks (IJCNN), Beijing, China

  8. Guarnieri S, Piazza F, Uncini A (1999) Multilayer feedforward networks with adaptive spline activation function. IEEE Trans Neural Netw 10(3):672–683

    Article  Google Scholar 

  9. Vecci L, Piazza F, Uncini A (1998) Learning and approximation capabilities of adaptive spline neural networks. Neural Netw 11(2):259–270

    Article  PubMed  Google Scholar 

  10. Ampazis N, Perantonis SJ (2002) Two highly efficient second-order algorithms for training feedforward networks. IEEE Trans Neural Netw 13(5):1064–1074

    Article  Google Scholar 

  11. Fukuoka Y, Matsuki H, Minamitani H, Ishida A (1998) A modified back-propagation method to avoid false local minima. Neural Netw 11(6):1059–1072

    Article  PubMed  Google Scholar 

  12. Lee H-M, Chen C-M, Huang T-C (2001). Learning efficiency improvement of back-propagation algorithm by error saturation prevention method. Neurocomputing 41(1–4):125–143

    Article  MATH  Google Scholar 

  13. Ng S-C, Cheung C-C, Leung S-H (2003) Integration of magnified gradient function and weight evolution with deterministic perturbation into back-propagation. IEE Electron Lett 39(5):447–448

    Article  Google Scholar 

  14. Rumelhart DE, Hinton GE, Williams RJ (1986) Learning internal representations by error propagation. In: Rumelhart DE, McClelland JL (eds) Parallel distributed processing: exploration in the microstructures of cognition, MIT Press, Cambridge, pp 318–362

    Google Scholar 

  15. Joost M, Schiffmann W (1998) Speeding up backpropagation algorithms by using cross-entropy combined with pattern normalization. Int J Uncertainty Fuzzyness Knowl-Based Syst 6(2):117–126

    Article  MATH  Google Scholar 

  16. van Ooyen A, Nienhuis B (1992) Improving the convergence of the backpropagation algorithm. Neural Netw 5:465–471

    Article  Google Scholar 

  17. Oh S-H (1997) Improving the error backpropagation algorithm with a modified error function. IEEE Trans Neural Netw 8(3):799–803

    Article  Google Scholar 

  18. Hertz J, Krogh A, Palmer RG (1991) Introduction to the theory of neural computation. Addison-Wesley, Redwood City

    MATH  Google Scholar 

  19. Palmieri F, Catello C, D’Orio G (1999) Inhibitory synapses in neural networks with sigmoidal nonlinearities. IEEE Trans Neural Netw 10(3):635–644

    Article  Google Scholar 

  20. Riedmiller M, Brun H (1993) A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In: Proceedings of the IEEE international conference on neural networks, vol 1, San Francisco, 28 March–1 April 1993

  21. Igel C, Huesken M (2003) Empirical evaluation of the improved rprop learning algorithms. Neurocomputing 50:105–123

    Article  MATH  Google Scholar 

  22. Treadgold NK, Gedeon TD (1998) Simulated annealing and weight decay in adaptive learning: the SARPROP algorithm. IEEE Trans Neural Netw 9(4):662–668

    Article  Google Scholar 

  23. Gorman RP, Sejnowski TJ (1988) Analysis of hidden units in a layered network trained to classify sonar targets. Neural Netw 1:75–89

    Article  Google Scholar 

  24. Karayiannis NB (1996) Accelerating the training of feedforward neural networks using generalized hebbian rules for initializing the internal representations. IEEE Trans Neural Netw 7(2):419–426

    Article  Google Scholar 

  25. Mandischer M (2002) A comparison of evolution strategies and backpropagation for neural network training. Neurocomputing 42(1–4):87–117

    Article  MATH  Google Scholar 

  26. Fahlman SE (1998) An empirical study of learning speed in back-propagation networks. Technical report CMU-CS-88-162, School of Computer Science, Carnegie Mellon University, Pittsburgh, USA

  27. http://www.microsoft.com

  28. http://www.mingw.org

  29. http://www.cs.virginia.edu/∼lcc-win32

  30. Rujan P (1997) Playing billiards in version space. Neural Comput 9:99–122

    Article  MATH  Google Scholar 

  31. Torres Moreno JM, Gordon MB (1998) Characterization of the sonar signals benchmarks. Neural Process Lett 7(1):1–4

    Article  Google Scholar 

  32. Perantonis SJ, Virvilis V (1999) Input feature extraction for multilayered perceptrons using supervised principal components analysis. Neural Process Lett 10(3):243–252

    Article  Google Scholar 

  33. Hasenjäger M, Ritter H (1999) Perceptron learning revisited: the sonar targets problem. Neural Process Lett 10(1):1–8

    Article  Google Scholar 

  34. Battiti R (1992) First and second-order methods for learning: between steepest descent and Newton’s method. Neural Comput 4(2):141–166

    Google Scholar 

  35. Battiti R (1989) Accelerated backpropagation learning: two optimization methods. Complex Syst 3:331–342

    MATH  Google Scholar 

  36. Johansson EM, Dowla FU, Goodman DM (1991), Backpropagation learning for multilayer feed-forward neural networks using the conjugate gradient method. Int J Neural Syst 2(4):291–301

    Article  Google Scholar 

  37. Hagan MT, Menhaj M (1994) Training feedforward networks with the Marquardt algorithm. IEEE Trans Neural Netw 5(6):989–993

    Article  Google Scholar 

  38. Tesauro G, Janssens B (1988) Scaling relationships in backpropagation learning. Complex Syst 2:39–84

    MATH  Google Scholar 

  39. Yang J-M, Kao C-Y (2001) A robust evolutionary algorithm for training neural networks. Neural Comput Applic 10(3):214–230

    Article  MATH  Google Scholar 

  40. Whitley D, Karunanithi N (1991) Generalization in feedforward neural networks. In: IJCNN-91-Seattle international joint conference on neural networks (IJCNN’91), vol 2, Seattle, 8–14 July 1991

  41. Perrone MP, Cooper LN (1993) When networks disagree: ensemble methods for hybrid neural networks. In: Mamone RJ (ed) Neural Networks for Speech and Image Processing, Chapman Hall, London, pp 126–142

    Google Scholar 

  42. Jiang J (1999) Image compression with neural network: a survey. Signal Process Image Commun 14(9):737–760

    Article  Google Scholar 

  43. Cybenko G (1989) Approximation by superposition of a sigmoid function. Math Control Signal Syst 2(4):303–314

    MATH  MathSciNet  Google Scholar 

  44. Chen DS, Jain RC (1994) A robust back propagation learning algorithm for function approximation. IEEE Trans Neural Netw 5(3):467–479

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This work was supported by the Thailand Research Fund (TRF).

Author information

Authors and Affiliations

  1. Department of Computer Engineering, Faculty of Engineering, Mahanakorn University of Technology, 51 Cheum-Sampan Road, Nong Chok, Bangkok, 10530, Thailand

    Khamron Sunat

  2. Advanced Virtual and Intelligent Computing (AVIC) Research Center, Department of Mathematics, Faculty of Science, Chulalongkorn University, Bangkok, 10330, Thailand

    Chidchanok Lursinsap

  3. Center for Advanced Computer Studies, The University of Louisiana at Lafayette, Lafayette, LA, 70504, USA

    Chee-Hung Henry Chu

Authors
  1. Khamron Sunat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chidchanok Lursinsap
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chee-Hung Henry Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Khamron Sunat.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sunat, K., Lursinsap, C. & Chu, CH.H. The p-recursive piecewise polynomial sigmoid generators and first-order algorithms for multilayer tanh-like neurons. Neural Comput & Applic 16, 33–47 (2007). https://doi.org/10.1007/s00521-006-0046-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-006-0046-x

Keywords

Search

Navigation