A dynamically-constructed fuzzy neural controller for direct model reference adaptive control of multi-input-multi-output nonlinear processes

Abstract

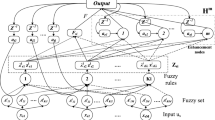
 Conventional industrial control systems are in majority based on the single-input-single-output design principle with linearized models of the processes. However, most industrial processes are nonlinear and multivariable with strong mutual interactions between process variables that often results in large robustness margins, and in some cases, extremely poor performance of the controller. To improve control accuracy and robustness to disturbances and noise, new design strategies are necessary to overcome problems caused by nonlinearity and mutual interactions. We propose to use a dynamically-constructed, feedback fuzzy neural controller (DCF-FNC) from the input–output data of the process and a reference model, for direct model reference adaptive control (MRAC) to deal with such problems. The effectiveness of our approach is demonstrated by simulation results on a real-world example of cold mill thickness control and is compared with the performances of the conventional PID controller and the cascade correlation neural network (CCN). Exploiting the advantage of intelligent adaptive control, both the CCN and our DCF-FNC significantly increases the control precision and robustness, compared to the linear PID controller, with our DCF-FNC giving the best results in terms of both accuracy and compactness of the controller, as well as being less computationally intensive than the CCN. We argue that our DCF-FNC feedback controller with both structure and parameter learning can provide a computationally efficient solution to control of many real-world multivariable nonlinear processes in presence of disturbances and noise.